Vectors

What is a Vector?

A vector is a fundamental mathematical concept defined by three distinct attributes: magnitude, direction, and orientation.

In other words, a vector is a segment to which a direction of traversal is fixed, that is, an oriented segment.

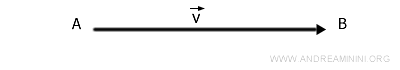
To indicate that it is a vector, I can denote the endpoints of the directed segment by placing an arrow above it (for example, \( \overrightarrow{AB} \)).

Alternatively, I can represent the vector with a lowercase letter, topped with an arrow (for example, \( \vec{v} \)).

The vector's initial point is termed the 'point of application', while its terminal point, marked by an arrowhead, signifies its endpoint.

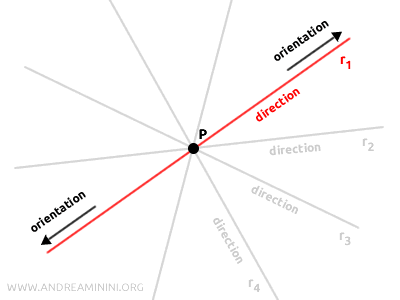
Consider the line segment of a vector. This segment delineates its direction, while the arrow provides insight into its orientation.

The length of the directed segment is called the magnitude and is denoted by placing the name of the vector between two vertical bars. For example, $ | \vec{v} | \ \ \text{or} \ \ | \overrightarrow{AB} | $

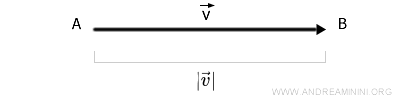
Sometimes the magnitude is simply denoted by the vector symbol without the arrow above it (for example, \( v \)).

The vector symbol \( \vec{v} \) should not be confused with its magnitude \( | \vec{v} | \). The symbol \( \vec{v} \) represents all the characteristics of the vector (direction, sense, length) and is a vector quantity. The magnitude of the vector \( | \vec{v} | \), on the other hand, indicates only the length and is a scalar quantity (e.g., a real number). Therefore, the magnitude \( | \vec{v} | \) is a component of the vector \( \vec{v} \).

Why are Vectors Important?

In physics, there are quantities inherently defined by their magnitude, direction, and orientation.

Examples of such quantities include spatial displacement, velocity, force, and acceleration.

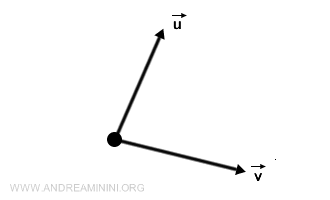
Vectors serve as the graphical representation of these quantities.

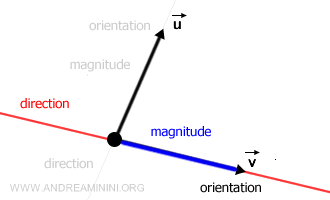
Each vector is uniquely characterized by its direction, orientation, and magnitude.

To visually represent a vector, one employs a directed line segment. Here's how to interpret it

• The arrow's orientation provides the vector's sense.
• The arrow's length, often termed its magnitude or norm, quantifies its intensity, and is scalar in nature.
• The line upon which the arrow is drawn offers insight into the vector's direction.

Distinguishing Between a Vector and its Magnitude. It's imperative to differentiate between a vector and its magnitude. Mistaking one for the other is a prevalent oversight but can lead to significant misunderstandings. While a vector encapsulates magnitude, direction, and orientation, its magnitude is solely a scalar value, representing only the vector's length. For clarity, two vectors might share an identical magnitude but can be distinct due to differing directions and orientations.

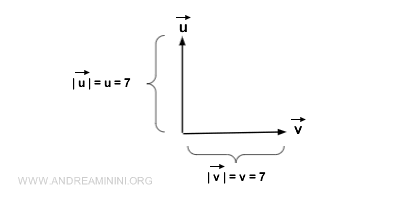
Conventionally, the magnitude is represented using the vector's symbol, sans the arrow, or by enclosing the vector symbol between vertical bars. In contrast, vectors are typically denoted with an arrow positioned above the letter or by rendering the letter in bold.

Although the mathematical scope of vectors is vast, the foundational concept remains consistent.

Vector Operations

Vectors support two primary operations:

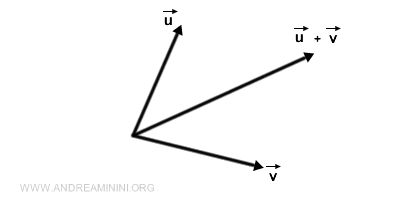
• Vector Addition
  The summation of two vectors yields a third, resultant vector.
  
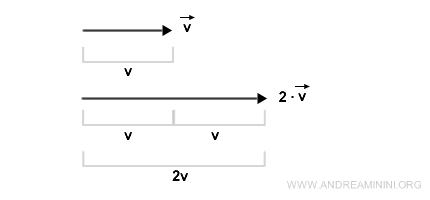
• Scalar Multiplication
  Multiplying a vector by a scalar (e.g., two) produces a vector with a magnitude that's proportionally adjusted, yet retains its original direction and orientation.
  

In both cases, the operations yield another vector as the result.

What is a Vector?

Vectors are fundamental concepts in mathematics and physics. To provide clarity, let's begin by examining vectors within a two-dimensional plane, which offers a more intuitive understanding.

In a two-dimensional space, specifically on the x,y plane, a vector is defined as a directed segment. This segment is characterized by three main attributes: its magnitude (often referred to as its length or norm), its direction, and its orientation.

Consider this illustration:

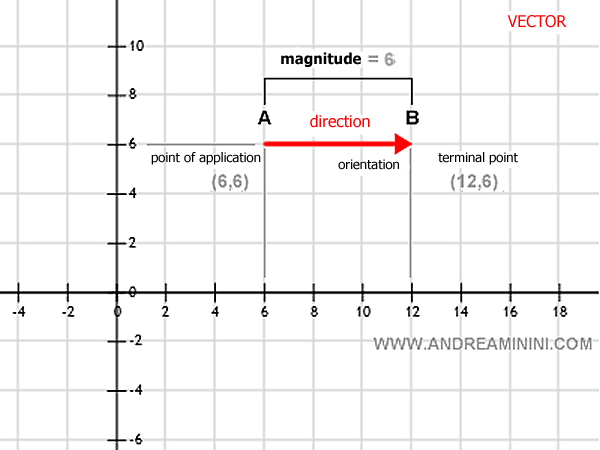
Example. On a given plane, imagine a segment that spans a length of 6 units, starting from point A (6,6) and ending at point B (12,6). By establishing a direction from A to B, we've effectively defined a vector.

Vectors are typically denoted in mathematics and physics using the initial and terminal points with an arrow overhead:

$$ \overrightarrow{AB} $$

Alternatively, they can be represented more succinctly as:

$$ AB $$

Distinguishing Between Applied and Free Vectors

Applied Vectors

An applied vector has a specific starting point, known as its point of application.

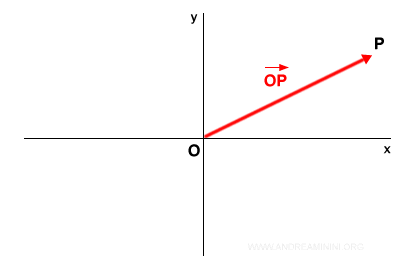
For instance, given a point P and an origin O on the plane, the vector that starts at O and ends at P is represented as the pair of points OP. This can be denoted as: $$ \overrightarrow{OP} $$ Or, using lowercase letters such as v, u, w, and so forth.

To illustrate:

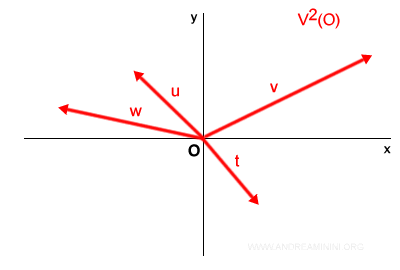
All vectors that share a common starting point, say O, can be grouped and symbolized as:

$$ V^2(O) $$

For a practical representation:

It's worth noting that while O represents the plane's origin, the vector's starting point can differ.

For instance, the directed segment AB has its starting point at A.

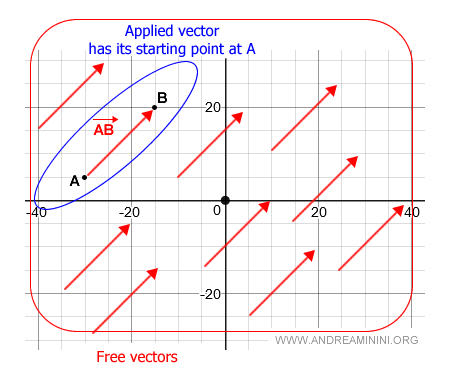
Free Vectors

In contrast, a free vector doesn't have a fixed starting point. Instead, it's defined solely by its direction and magnitude.

All such vectors within a plane are collectively represented by:

$$ V $$

Note. A free vector essentially encapsulates all vectors belonging to a specific equivalence class, serving as the representative of that class.

Defining a Vector in Mathematics

A vector is an element of a vector space. Within the realm of real vector spaces, a vector is an ordered n-tuple of real numbers ( x₁, ... , x_n ).

The real numbers within a vector are referred to as its components.

A Practical Example

Here are some examples of vectors composed of two components (n=2) within the field of real numbers:

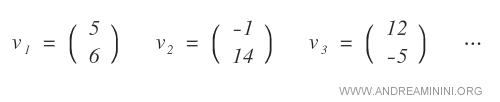
The collection of all vectors with two components constitutes the real vector space ( R² = RxR ).

This ( R² ) space corresponds to all points on the Cartesian plane.

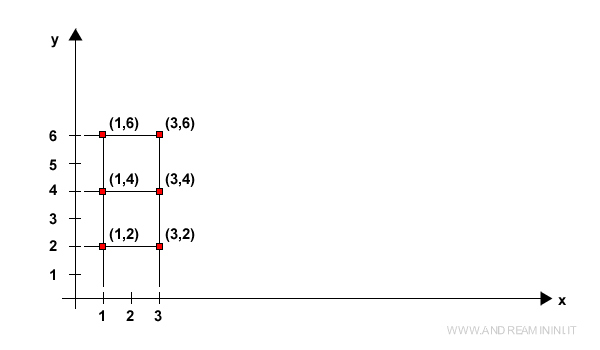
Indeed, every pair of real numbers ( x₁, x₂ ) corresponds to a unique point ( x, y ) on the Cartesian plane.

Vector Addition

Given two numeric vectors each with n components:

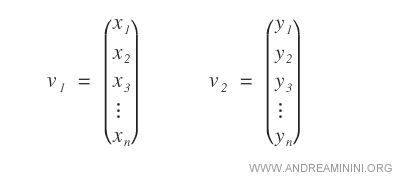
The sum of the vectors results in a vector with n components, where each component ( z_n ) is the numeric sum of the corresponding components ( x_n + y_n ).

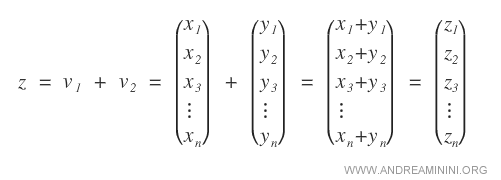
Scalar Multiplication of a Vector

Given a vector v with n components and any real scalar α, the product of the vector and the scalar results in a vector where each component x_n is multiplied by the scalar α.

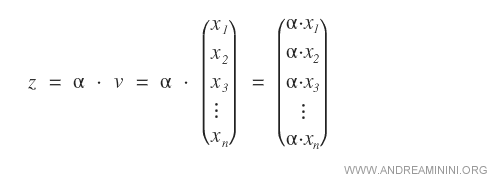
Vector Representation

In a two-dimensional space, vectors can be depicted on the Cartesian plane.

Two geometric vectors OE₁ and OE₂ are linearly independent if they lie on different lines passing through the origin.

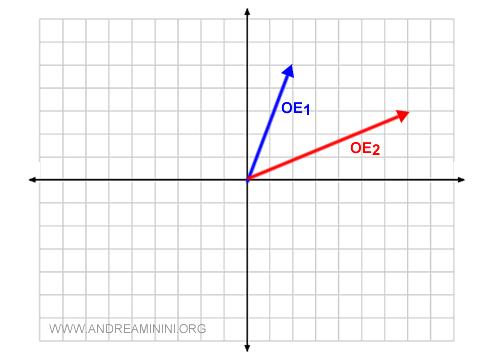
Two independent vectors form a basis for the vector space V²O because their linear combination can generate all the free vectors in the two-dimensional vector space V².

$$ B = \{ OE_1 , OE_2 \} $$

Every point P on the plane corresponds to a numeric vector v(x,y) that identifies the coordinates C_v(x,y) of the vector OP relative to the basis { OE₁, OE₂ }.

$$ OP = a_1 \cdot OE1 + a_2 \cdot OE2 $$

Conversely, every vector v(x,y) corresponds to a point P on the plane through linear combination.

A Practical Example

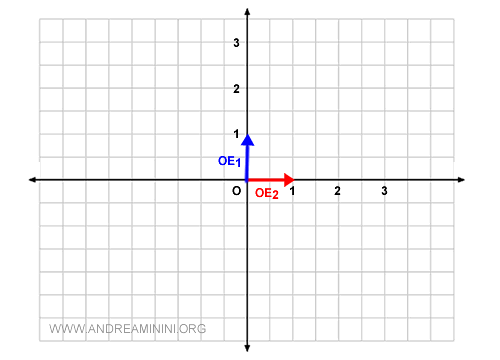
I use the vectors v₁=(0,1) and v₂(1,0) as the vector basis B, which are OE₁ and OE₂ respectively.

$$ B = \{ v_1 , v_2 \} \\ v_1 = \begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ v_2 = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

Besides being linearly independent, v₁ and v₂ are also orthogonal to each other, making graphical representation easier.

Now, I want to represent point P on the graph.

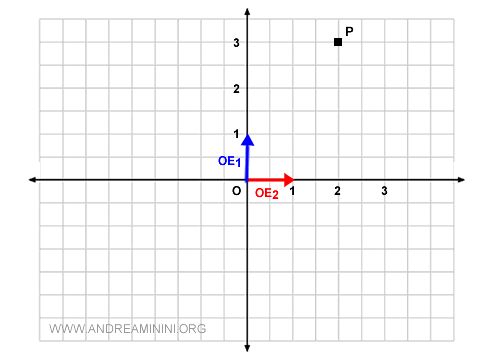
Like every point on the plane, point P corresponds to a vector that passes through the origin (O).

In this case, it's the geometric vector OP.

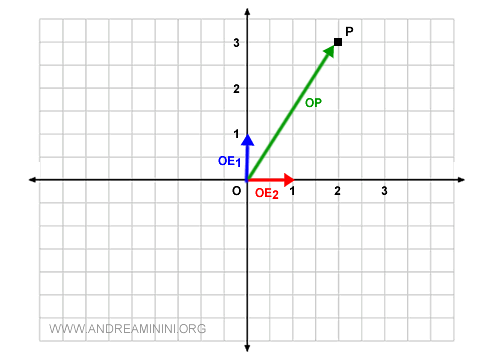
The vector \( OP \) is linearly dependent on the basis vectors { OE₁, OE₂ } because it can be represented through their linear combination.

In essence, there exist two scalars c₁ and c₂, known as coordinates, such that:

$$ \overrightarrow{OP} = c_1 OE_1 + c_2OE_2$$

$$ \overrightarrow{OP} = c_1 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + c_2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = 3 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + 2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = \begin {pmatrix} 0 \\ 3 \end{pmatrix} + \begin {pmatrix} 2 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = \begin {pmatrix} 2 \\ 3 \end{pmatrix} $$

In this case, the solution is straightforward.

The coordinates are c₁=3 and c₂=2, which means three times the vector OE₁ and twice the vector OE₂.

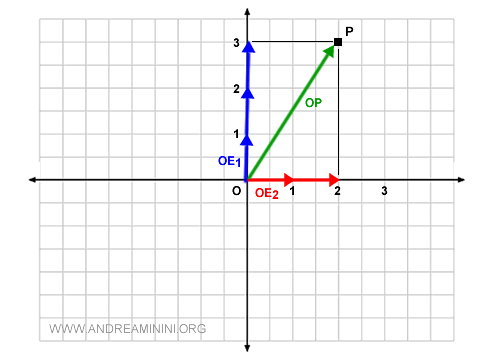
The correspondence between point P and vector OP is denoted by the following equivalence relation:

$$ \overrightarrow{OP} \equiv P \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Similarly, I can represent any other point on the Cartesian plane R x R or R².

Note. The correspondence between points and vectors is invaluable, as it allows us to study the geometric properties of points and vectors using linear algebra.

Vectors in Multidimensional Spaces

In mathematics, vectors aren't confined to the two-dimensional plane we often visualize. They can exist and be defined within multidimensional spaces.

Two-dimensional Vectors

In a two-dimensional space, denoted as R², a vector is characterized by the difference between its initial and terminal points on a plane.

$$ V \{ x_2-x_1, y_2-y_1 \} $$

Example

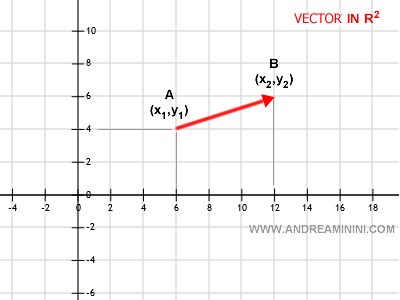
Take, for instance, a vector on the plane: $$ V \{ x_2-x_1, y_2-y_1 \} $$ Breaking it down: $$ V \{ 12-6, 6-4 \} $$ We get: $$ V \{ 6, 2 \} $$

 

Three-dimensional Vectors

Transitioning to a three-dimensional space, or R³, the representation remains algebraically consistent, but with the inclusion of an additional z-coordinate.

$$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$

For brevity, the vector's elements can directly denote the difference, sometimes referred to as acceleration.

$$ V \{ x, y, z \} $$

Where:

$$ x=x_2-x_1 $$ $$ y=y_2-y_1 $$ $$ z=z_2-z_1 $$

This notation becomes increasingly valuable when delving into higher dimensions.

Example

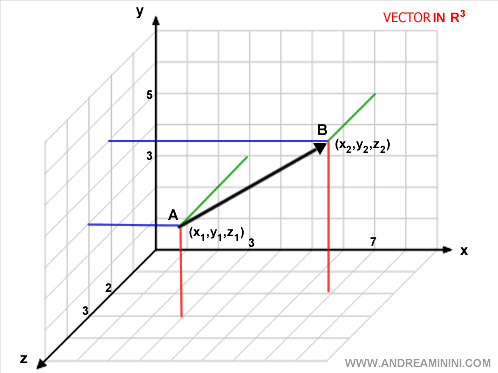
Consider a vector in a 3D space (x,y,z): $$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$ Given points A=(3,3,3) and B=(7,5,2): $$ con A=(3,3,3) , B=(7,5,2) $$ $$ V \{ 7-3, 5-3, 2-3 \} $$ This results in: $$ V \{ 4, 2, -1 \} $$

Vectors in n-dimensional Spaces

Extending this concept to n-dimensional spaces, represented as Rⁿ, we have:

$$ V \{ x_1, x_2, x_2, ... , x_n \} $$

Yet, visualizing these vectors geometrically poses a challenge.

Our human experience is rooted in three dimensions, with the fourth often conceptualized as time. Beyond that, our ability to geometrically grasp higher dimensions diminishes. This isn't a failing, but rather a testament to the complexity of the mathematical landscape. To navigate these intricate dimensions, we often resort to simplifications or alternative representation techniques.

Thus, n-dimensional vectors are typically represented as an ordered n-tuple of n elements:

$$ V \{ x_1, x_2, x_2, ... , x_n \} $$

Where each element, from x₁ to x_n, can be any real number.

For Instance

$$ V \{ 4, 2, -1, 7 , 3 \} $$

The exploration of multidimensional vectors is a cornerstone of linear algebra.