Orthogonal Vectors

Orthogonal vectors are related by orthogonality (perpendicularity) to each other.

In a real vector space, two vectors v₁, v₂ are orthogonal if their dot product is zero. $$ <v_1,v_2> = 0 $$

The symbol of an inverted T indicates the orthogonality between two vectors.

$$ v_1 \perp v_2 $$

Note: A zero dot product is a necessary but not sufficient condition for orthogonality. It's also essential that neither of the vectors is a zero vector, meaning each must have a nonzero magnitude. For instance, the dot product of any vector with a zero vector equals zero, but the two vectors are not orthogonal. $$ < \vec{v} , \vec{0} > = 0 $$

An Example of Orthogonal Vectors

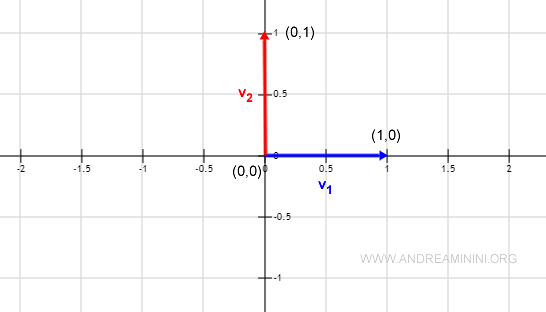
In the vector space V=R² over the field K=R, consider two vectors:

$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$

The Euclidean dot product <v₁,v₂> of these two vectors equals zero.

$$ <v_1,v_2> = 1·0 + 0·1 = 0 $$

Thus, these two vectors are orthogonal.

Note: These vectors v₁, v₂ can be represented in the Cartesian plane with the origin point O (0,0) as a reference. The graphical representation clearly shows that the vectors are geometrically perpendicular to each other.

 

Example 2

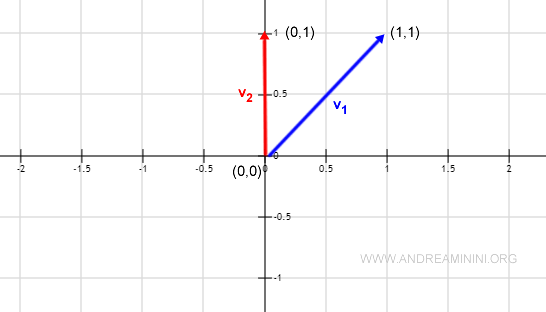
Now, let's consider another pair of vectors.

$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$

Their dot product is not zero.

$$ <v_1,v_2> = 1·0 + 1·1 = 0+1 = 1 $$

Therefore, these vectors are not orthogonal.

Note: Representing these vectors on the Cartesian plane, it's immediately apparent that they are not geometrically perpendicular.

 

The Cosine of the Angle and Orthogonality

When both vectors are different from the zero vector, there's a close relationship between the cosine of the angle formed by vectors v₁ and v₂, their dot product, and the norm.

$$ cos(v_1,v_2) = \frac{ <v_1,v_2> } { ||v_1|| \cdot ||v_2|| }$$

By convention, if one of the vectors v₁ or v₂ is zero, the cosine is set to zero.

$$ cos(v_1,v_2) := 0 \:\:if \:\:v_1=0_V \:\:or\:\: v_2=0_V $$

A Practical Example

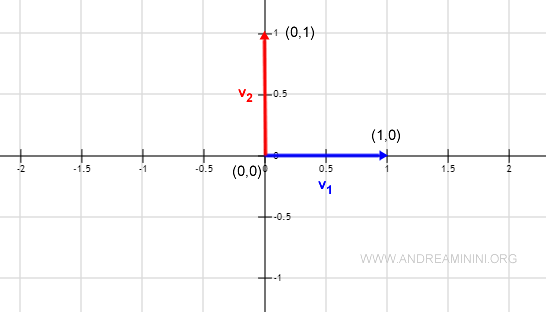
Let's calculate the cosine of the angle for these vectors:

$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$

Their dot product is:

$$ <v_1,v_2> = 1·0 + 0·1 = 0 $$

While the norms of the vectors are:

$$ ||v_1|| = \sqrt{1^2+0^2} = 1 \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$

Hence, the cosine of the angle formed by these two vectors is:

$$ cos(v_1,v_2) = \frac{ 0 } { 1 } = 0 $$

Indeed, it's a 90° angle and the cosine equals 0.

Example 2

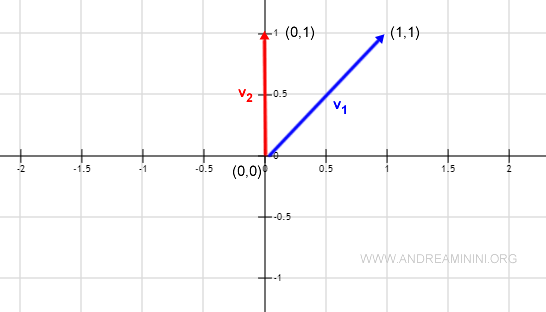
Now, let's calculate the cosine for another pair of vectors:

$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$

Their dot product is:

$$ <v_1,v_2> = 1·0 + 1·1 = 0+1 = 1 $$

While the norms of the vectors are:

$$ ||v_1|| = \sqrt{1^2+1^2} = \sqrt{2} \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$

Therefore, the cosine of the angle formed between these two vectors is:

$$ cos(v_1,v_2) = \frac { 1 } { \sqrt{2} \cdot 1 } = \frac {1} { \sqrt{2} } $$

Indeed, these vectors form a 45° angle.

The Difference Between Perpendicularity and Orthogonality

The term "orthogonality" is synonymous with "perpendicularity."

However, "perpendicularity" is more often used in a geometric context, while "orthogonality" is a more abstract concept applied in non-geometric contexts as well.

Orthogonal and Orthonormal Bases

Orthogonal vectors form orthogonal and orthonormal bases.

• The orthogonal base is composed of orthogonal vectors.
• The orthonormal base is an orthogonal base with unit norm vectors.