Orthogonal Complement

The orthogonal complement, or orthogonal supplement, is a subspace W* of the vector space V comprising vectors that are orthogonal to every vector w in a vector subspace W.

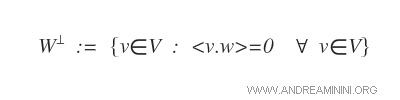
The orthogonal supplement is denoted by an inverted T symbol.

In a finite-dimensional vector space V, the vector subspaces W* and W are supplementary subspaces to each other.

In other words, the direct sum of subspaces W* and W equals the vector space V.

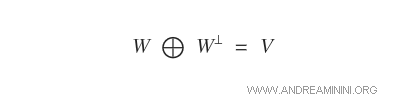
Calculating Vectors of the Orthogonal Complement

A vector v in V belongs to the orthogonal complement W* if and only if v is orthogonal to all elements of the base B_W = { w_1 ,..., w_n } of the vector subspace W.

This is equivalent to solving a system of Cartesian equations.

$$ \begin{cases} <v,w_1> = c_{11} v_1 + ... + c_{1n} v_n = 0 \\ <v,w_2> = c_{21} v_1 + ... + c_{2n} v_n = 0 \\ ... \\\ <v,w_k> = c_{k1} v_1 + ... + c_{kn} v_n = 0 \end{cases} $$

Here, the coefficients c represent elements of each vector w in the base of subspace W.

$$ W = B \{ w_1, w_2, ... , w_k \} $$

Meanwhile, the vector v is a generic vector in vector space V, which may or may not belong to the orthogonal complement.

Note. The equations are homogeneous because for a vector v to be orthogonal to vector w, the scalar product <v,w> must equal 0.

An Example Calculation

In a vector space V=R⁴ over the field K=R, consider a vector subspace W generated by the following base:

$$ B_w = \{ w_1 , w_2 \} \\ w_1 = ( 1,1,1,1 ) \\ w_2 = ( 1,0,1,0 ) $$

I need to find vectors v in V that are orthogonal to the vectors of base B.

$$ v* = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} $$

Since there are two base vectors, this entails solving the following system:

$$ \begin{cases} x_1+x_2+x_3+x_4=0 \\ x_1+x_3=0 \end{cases} $$

$$ \begin{cases} (-x_3)+x_2+x_3+x_4=0 \\ x_1=-x_3 \end{cases} $$

$$ \begin{cases} x_2=-x_4 \\ x_1=-x_3 \end{cases} $$

This leads to the vectors of the base of the orthogonal complement W*

$$ v* = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} = B_{W*} \{ \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} \} $$

All vectors generated from this base belong to the orthogonal complement.

Example. The vector v(3,2,-3,-2) belongs to the orthogonal complement $$ v = \begin{pmatrix} 3 \\ 2 \\ -3 \\ -2 \end{pmatrix} = 2 \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix} + 3 \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} $$ as it is generated by a linear combination of two scalar numbers (2,3) with the base of the orthogonal complement