Orthogonal Bases

In vector space B{v,w}, an orthogonal basis consists of orthogonal vectors. This means the dot product of any two vectors is zero. $$ <v,w>=0 \:\:\:\: \forall \ v,w $$

The orthogonality condition applies to each pair of vectors in the set.

An Example of an Orthogonal Basis

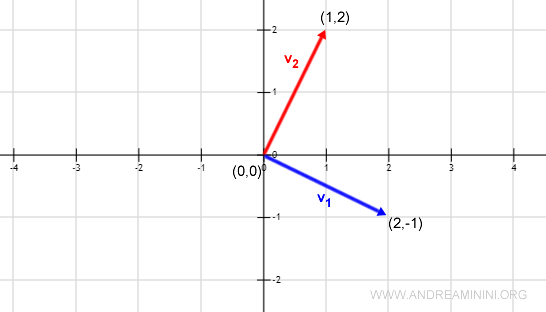
This basis is a practical example of an orthogonal basis, comprising orthogonal vectors.

$$ B = \{ \begin{pmatrix} 2 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \end{pmatrix} \} $$

$$ <v_1,v_2> = 2·(1) + (-1)·2 = 2 - 2 = 0 $$

Note. A quick glance at their representation on a plane immediately reveals the perpendicularity of these two vectors.

Differentiating Between Orthogonal and Orthonormal Bases

An orthogonal basis becomes an orthonormal basis when it consists of orthogonal vectors with unit norm, i.e., their dot product equals either 1 or 0.

Example

This orthogonal basis is also orthonormal:

$$ B = \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \} $$

The dot product of different vectors is zero.

$$ <v,w>= ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0+0 = 0 $$

The dot product equals 1 when the vectors are the same.

$$ <v,v>= ( 1 \cdot 1 ) + ( 0 \cdot 0 ) = 1+0 = 1 $$

$$ <w,w>= ( 0 \cdot 0 ) + ( 1 \cdot 1 ) = 0+1 = 1 $$

Transforming an Orthogonal Basis into an Orthonormal One

Any orthogonal basis can be transformed into an orthonormal basis by normalizing the vectors.

Note. For further information, see how to transform an orthogonal basis into an orthonormal basis.