Transforming a Basis into an Orthogonal Basis
To transform any vector basis into an orthogonal vector basis, it's enough to project one vector onto the other non-zero vector using Fourier coefficients.
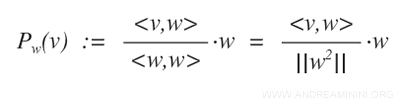
Where the Fourier coefficient is the ratio
$$ \frac{<v,w>} {<w,w>} $$
Fourier coefficients are fundamental in the Gram-Schmidt orthogonalization method.
Starting from the projection Pw(v), an orthogonal basis can be constructed from any basis using the following formula:
$$ w_1 = v_1 $$ $$ w_i = v_i - \sum_{ j=1}^{i-1} P_wj(v_i) \:\:\:\: per \:\:\:\: i=2,...n $$
Of course, the resulting orthogonal basis isn't the only possibility, as it depends on the order of vectors in the base.
Note. The orthogonal basis obtained has specific properties defined by the Gram-Schmidt orthogonalization. For instance, it's a generator of the same vector space. If the vectors in the initial basis are linearly independent, they remain independent in the orthogonal basis after transformation.
Once the orthogonal basis is obtained, it can finally be transformed into an orthonormal basis.
The Fourier Coefficients
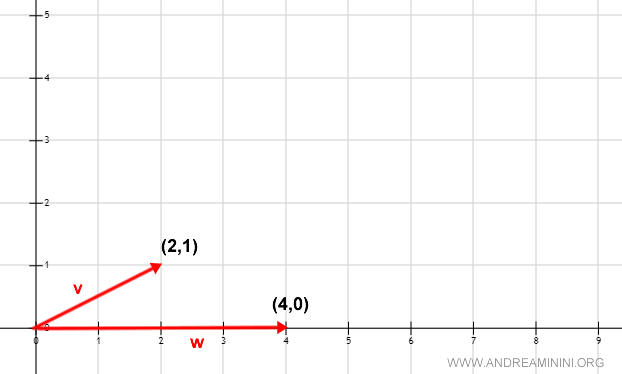
In a vector space V=R2 over K=R, I have a vector basis B consisting of the following vectors:
$$ B = \{ v , w \} = \{ ( 2,1 ) , ( 4,0 ) \} $$
It's not an orthogonal basis, because the scalar product equals 8.
$$ <v,w> = (2*4)+(1*0) = 8 $$
Observing the graphical representation on the plane, the non-orthogonality (non-perpendicularity) of the vectors is evident.
The scalar product induces the norm ||·||
To transform it into an orthogonal basis, consider the orthogonal projection Pw(v) of vector v onto w.
$$ P_w(v) = (2,0 ) $$
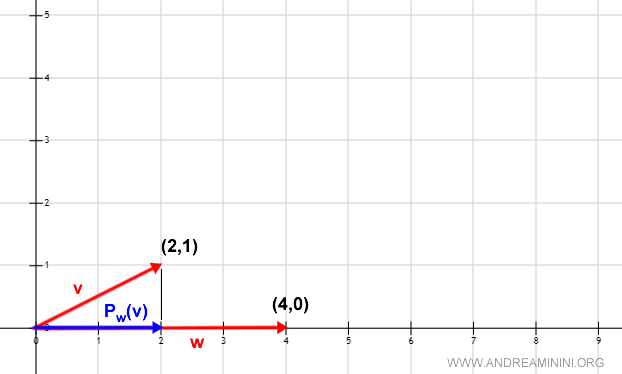
The vector Pw(v) is a multiple of the vector w, meaning there exists a scalar k in R such that
$$ k*P_w(v)=w $$
Note. In this simple example, the scalar is apparent; multiplying Pw(v) by 2 yields the vector w.
Then, calculate the difference between vector v and the orthogonal projection Pw(v)
$$ v' = v - P_w \\ v' = (2,1) - (2,0) \\ v' = (0,1) $$
Thanks to the difference, an orthogonal vector to Pw(v) is obtained.
For simplicity, let's denote it as v'.
A graphical analysis easily confirms the orthogonality between v' and the projection Pw(v).
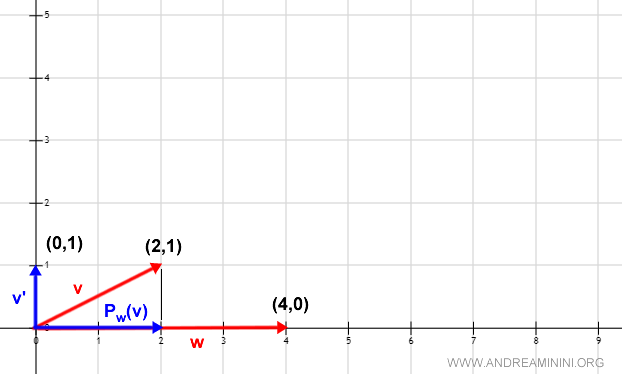
Since v' is orthogonal to w, the scalar product w(v)> is zero.
$$ <v',P_w(v)> = 0 $$
Substituting v' with v-Pw(v), I get
$$ <v',P_w(v)> = 0 \\ <v-P_w(v),P_w(v)> = 0 $$
According to the third property of the scalar product: $$ <a+b, c> = <a,c>+<b,c> $$
Rewriting the equation in the following way:
$$ <v,P_w(v)> - <P_w(v),P_w(v)> = 0 $$
Knowing that Pw(v) is a multiple of w
$$ P_w(v) = k \cdot w $$
I can substitute Pw(v) with kw
$$ <v,kw> - <kw,kw> = 0 \\ <v,kw> - k<w,w> = 0 $$
According to the fourth property of the scalar product: $$ <ka,b> = k<a,b>$$
Thus, I can transform the equation in the following way:
$$ k \cdot <v,w> - k<w,w> = 0 $$
Aside from the case of the vector (k=0) excluded beforehand, this equation is satisfied when the scalar k assumes the following value:
$$ k = \frac{<v,w>}{<w,w>} $$
This scalar is known as the Fourier coefficient of vector v with respect to w.
Therefore, the orthogonal projection of vector v onto w equals
$$ P_w(v) := \frac{<v,w>}{<w,w>} \cdot w = \frac{<v,w>}{||w^2||} \cdot w $$
Returning to the previous example, the Fourier coefficient
$$ k = \frac{<v,w>}{<w,w>} = \frac{ 8 }{ 16 } = \frac{ 1 }{ 2 } $$
the orthogonal projection of vector v onto w is:
$$ P_w(v) = \frac{<v,w>}{<w,w>} \cdot w = \frac{1}{2} \cdot (4,0) = (2,0) $$
Gram-Schmidt Orthogonalization
The Gram-Schmidt orthogonalization method allows me to use Fourier coefficients to transform any vector basis into an orthogonal basis.
Given a generator L of n vectors {vi} in the vector space V over the field K=R, there always exists a generator L' of n mutually orthogonal vectors {wi} equivalent to L. $$ L\{v_1,...,v_n\} = L'\{w_1,...,w_n\} \\ <w_i,w_j>=0 \:\: for \:\: i \ne j $$
If the vectors of the initial generator L were linearly independent, then the orthogonal vectors of the generator L' are also linearly independent.
Therefore, if L is a basis, then L' is also a basis.
The Formula for Finding the Orthogonal Basis Vectors
To find the orthogonal vectors, the method uses the following formula:
The first vector v1 of the generator L remains the same (w1=v1) in the generator L'. $$ w_1 = v_1 $$ The subsequent vectors are orthogonalized using orthogonal projection and the Fourier coefficient. $$ w_i = v_i - \sum_{ j=1}^{i-1} P_{wj}(v_i) \:\:\:\: for \:\:\:\: i=2,...n $$
The end result is an orthogonal basis of the vector space V.
Note. Naturally, the basis is not unique, as it also depends on the positioning of vectors in the initial basis.
A Practical Example
In the vector space V=R3 over the field K=R, I have the following basis:
$$ B = \{ v_1 , v_2, v_3 \} = \{ ( 1,1,1 ) , ( -1,1,0 ) , ( 1,2,1 ) \} $$
It consists of three linearly independent vectors.
These vectors are not orthogonal as their scalar product is not zero and the norm is different from 1.
The scalar products of the basis vectors
$$ < v_1 , v_2 > = 1 \cdot -1 + 1 \cdot 1 + 1 \cdot 0 = 0 \\ < v_1 , v_3 > = 1 \cdot 1 + 1 \cdot 2 + 1 \cdot 1 = 4 \\ < v_2 , v_3 > = -1 \cdot 1 + 1 \cdot 2 + 0 \cdot 1 = 1 $$
To calculate the orthogonal basis B', I follow the Gram-Schmidt method.
$$ B' = \{ w_1 ,w_2,w_3 \} $$
The first vector of the orthogonal basis is the same as the first vector of the starting basis.
$$ w_1 = v_1 = (1,1,1) $$
The second vector of the orthogonal basis is determined using the Gram-Schmidt formula.
$$ w_i = v_i - \sum_{ j=1}^{i-1} P_{wj}(v_i) \:\:\:\: for \:\:\:\: i=2,...n $$
$$ w_2 = v_2 - \sum_{ j=1}^{2-1} P_{wj}(v_2) \:\:\:\: for \:\:\:\: i=2,...n $$
$$ w_2 = v_2 - P_{w1}(v_2) $$
The orthogonal projection Pw of vector v2 is as follows:
$$ P_{w1}(v_2) = \frac{<v_2,w_1>} {<w_1,w_1>} \cdot w_1 $$
$$ P_{w1}(v_2) = \frac{< ( -1,1,0 ) , (1,1,1) >} {< (1,1,1) , (1,1,1) >} \cdot (1,1,1) $$
$$ P_{w1}(v_2) = \frac{ -1 \cdot 1 + 1 \cdot 1 + 0 \cdot 0 } { 1^2 + 1^2 + 1^2 } \cdot (1,1,1) $$
$$ P_{w1}(v_2) = \frac{ 0 } { 3 } \cdot (1,1,1) $$
$$ P_{w1}(v_2) = 0 $$
Thus, returning to the Gram-Schmidt formula, I can determine the second vector w2 of the orthogonal basis B'.
$$ w_2 = v_2 - P_{w1}(v_2) $$
$$ w_2 = ( -1,1,0 ) - 0 $$
$$ w_2 = ( -1,1,0 ) $$
Now, I can calculate the third and final vector w3 of the orthogonal basis using the Gram-Schmidt formula.
$$ w_i = v_i - \sum_{ j=1}^{i-1} P_{wj}(v_i) \:\:\:\: for \:\:\:\: i=2,...n \\ w_3 = v_3 - \sum_{ j=1}^{3-1} P_{wj}(v_3) \:\:\:\: for \:\:\:\: i=2,...n \\ w_3 = v_3 - P_{w1}(v_3) - P_{w2}(v_3) $$
The orthogonal projection Pw1 of vector v3 is as follows:
$$ P_{w1}(v_3) = \frac{<v_3,w_1>} {<w_1,w_1>} \cdot w_1 $$
$$ P_{w1}(v_3) = \frac{<(1,2,1),(1,1,1)>} {<(1,1,1),(1,1,1)>} \cdot (1,1,1) $$
$$ P_{w1}(v_3) = \frac{ 1 \cdot 1 + 2 \cdot 1 + 1 \cdot 1 } { 1 \cdot 1 + 1 \cdot 1 + 1 \cdot 1 } \cdot (1,1,1) $$
$$ P_{w1}(v_3) = \frac{ 4 } { 3 } \cdot (1,1,1) $$
$$ P_{w1}(v_3) = ( \frac{ 4 } { 3 } \cdot 1 , \frac{ 4 } { 3 } \cdot 1 , \frac{ 4 } { 3 } \cdot 1 ) $$
$$ P_{w1}(v_3) = ( \frac{ 4 } { 3 } , \frac{ 4 } { 3 } , \frac{ 4 } { 3 } ) $$
The orthogonal projection Pw2 of the vector v3 is as follows:
$$ P_{w2}(v_3) = \frac{<v_3,w_2>} {<w_2,w_2>} \cdot w_2 $$
$$ P_{w2}(v_3) = \frac{<(1,2,1),( -1,1,0 )>} {<( -1,1,0 ),( -1,1,0 )>} \cdot ( -1,1,0 ) $$
$$ P_{w2}(v_3) = \frac{1 \cdot -1 + 2 \cdot 1 + 1 \cdot 0 } { -1 \cdot -1 + 1 \cdot 1 + 0 \cdot 0 } \cdot ( -1,1,0 ) $$
$$ P_{w2}(v_3) = \frac{ 1 } { 2 } \cdot ( -1,1,0 ) $$
$$ P_{w2}(v_3) = ( -1 \cdot \frac{ 1 } { 2 },1 \cdot \frac{ 1 } { 2 },0 \cdot \frac{ 1 } { 2 } ) $$
$$ P_{w2}(v_3) = ( - \frac{ 1 } { 2 }, \frac{ 1 } { 2 }, 0 ) $$
With this, I can now compute the third and final vector w3 of the orthogonal basis using the Gram-Schmidt process.
$$ w_3 = v_3 - P_{w1}(v_3) - P_{w2}(v_3) \\ w_3 = (1,2,1) - ( \frac{ 4 } { 3 } , \frac{ 4 } { 3 } , \frac{ 4 } { 3 } ) - ( - \frac{ 1 } { 2 }, \frac{ 1 } { 2 }, 0 ) \\ w_3 = (1 - \frac{ 4 } { 3 } + \frac{ 1 } { 2 } ,2 - \frac{ 4 } { 3 } - \frac{ 1 } { 2 } , 1 - \frac{ 4 } { 3 } - 0 ) \\ w_3 = ( \frac{ 1 } { 6 } , \frac{ 1 } { 6 } , - \frac{ 1 } { 3 } ) \\ w_3 = ( \frac{ 1 } { 6 } , \frac{ 1 } { 6 } , - \frac{ 1 } { 3 } ) $$
In conclusion, the vectors of the orthogonal basis B' are as follows:
$$ B' = \{ w_1, w_2, w_3 \} $$ $$ B' = \{ (1,1,1), (-1,1,0) , ( \frac{ 1 } { 6 } , \frac{ 1 } { 6 } , - \frac{ 1 } { 3 } ) \} $$
This gives us an equivalent orthogonal basis.
Note. This is just one of many possible orthogonal bases. If I were to reverse the order of the vectors in basis B, I would get a different orthogonal basis B'.
Verification
For assurance, let's verify whether the vectors w1, w2, w3 are indeed orthogonal by calculating their scalar products.
$$ < w_1 ,w_2 > = 1 \cdot -1 + 1 \cdot 1 + 1 \cdot 0 = 0 \\ < w_1 , w_3 > = 1 \cdot \frac{ 1 } { 6 } + 1 \cdot \frac{ 1 } { 6 } + 1 \cdot \frac{ -1 } { 3 } = 0 \\ < w_2 ,w_3 > = -1 \cdot \frac{ 1 } { 6 } + 1 \cdot \frac{ 1 } { 6 } + 0 \cdot \frac{ 1 } { 6 } = 0 $$
The scalar products are all zero, confirming that the vectors w1, w2, w3 are orthogonal to each other.
Are the vectors w1, w2, w3 also orthonormal?
No, the vectors are not orthonormal since their norms are not equal to 1.
$$ || w_1 || = \sqrt{ 1^2+1^2+1^2 } = \sqrt{3} \\ || w_2 || = \sqrt{ -1^2+1^2+0^2 } = \sqrt{ 2 } \\ || w_3 || = \sqrt{ ( \frac{ 1 } { 6 }) ^2+( \frac{ 1 } { 6 })^2+(- \frac{ 1 } { 3 })^2 }= \sqrt{ \frac{ 1 } { 6 } } $$
However, it is possible to transform this orthogonal basis into an orthonormal one by normalizing the three vectors.
See this other example for the procedure of transforming an orthogonal basis into an orthonormal one.
