Orthonormal Basis
An orthonormal basis of a vector space B{v,w} is defined as a set of orthogonal vectors $$ <v,w>=0 \:\:if\:\: v \ne w $$ and with unit norm $$ || \vec{v} || = || \vec{w} || = 1 $$
In other words, there are two key conditions for an orthonormal basis:
- The vectors in the basis have unit norm, meaning their magnitude (length) is exactly 1.
- The vectors in the basis are distinct and orthogonal to each other; in such cases, their dot product <v,w>=0 is zero.
Note. Vectors in orthonormal bases are also referred to as unit norm vectors because the norm of both vectors equals 1. $$ ||v|| = 1 $$ $$ ||w|| = 1 $$ This property can be inferred from the unit dot product <v,w>=1 when vectors v and w are the same. Any norm induced by the dot product is $$ ||v|| = \sqrt{ <v,v> } $$ This condition is often added. If the vectors in the basis are identical v=w, their dot product <v,w>=1 must equal 1.
Example of an Orthonormal Basis
This basis is a practical example of an orthonormal basis.
It represents a canonical basis.
$$ B = \{ \vec{v_1} \ , \ \vec{v_2} \} = \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \} $$
Both vectors have unit norm.
$$ ||\vec{v}|| = \sqrt{1^2+0^2} = 1 $$
$$ ||\vec{w}|| = \sqrt{0^2+1^2} = 1 $$
The two basis vectors are distinct and their dot product is zero.
$$ <v,w>= ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0+0 = 0 $$
Therefore, it forms an orthonormal basis.
Graphically, the two vectors form a 90° angle (orthogonal vectors) and have a length (magnitude) of 1.
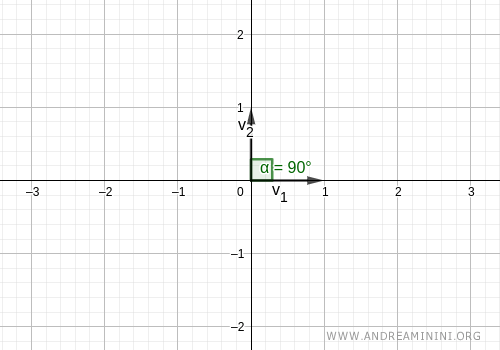
Note. In an orthonormal basis, the vectors are unit norm vectors. This is another way to verify the orthonormality of the basis. $$ ||v|| = \sqrt{1^2+0^2}=1 $$ $$ ||w|| = \sqrt{0^2+1^2}=1 $$
The Difference Between Orthogonal and Orthonormal Bases
An orthonormal basis is always an orthogonal basis as well, since it consists of orthogonal vectors.
However, the reverse is not necessarily true. An orthogonal basis is not guaranteed to be an orthonormal basis.
Example
This basis is orthogonal because
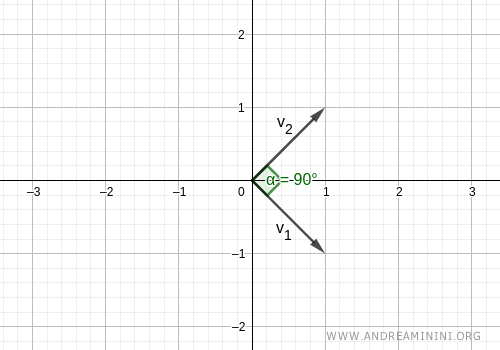
$$ B = \{ \begin{pmatrix} 1 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 1 \end{pmatrix} \} $$
as they are two distinct vectors and their dot product is zero
$$ <v,w>= ( 1 \cdot 1 ) + ( -1 \cdot 1 ) = 1-1 = 0 $$
Consequently, the two vectors form a 90° angle, meaning they are orthogonal vectors
However, this is not an orthonormal basis because the vectors do not all have unit norm.
$$ ||v_1|| = \sqrt{1^2+(-1)^2}=\sqrt{2} $$ $$ ||v_2|| = \sqrt{1^2+1^2}=\sqrt{2} $$
Graphically, this means the length (magnitude) of the vectors is not equal to 1.
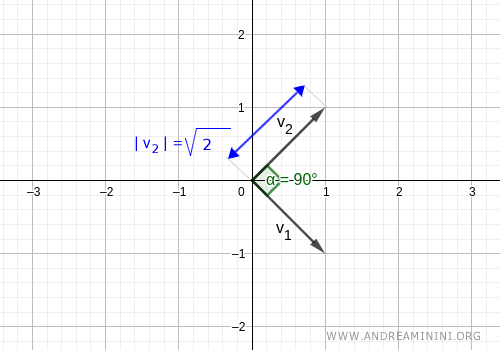
While forming a 90° angle (orthogonal vectors), they are not orthonormal.
Note. Any orthogonal basis can be transformed into an orthonormal basis by normalizing the vectors that make up the basis. For more information, see how to transform an orthogonal basis into an orthonormal one.
