Dot product of two vectors

The dot product (or scalar product) between two vectors yields a scalar value. It's calculated by multiplying the magnitude of one vector by the magnitude of the projection of the second vector onto the first. $$ \vec{v_1} \cdot \vec{v_2} = | \vec{v_1} | \cdot | \vec{v_2} | \cdot \cos \theta $$ In this equation, θ is the angle between the two vectors.

Often referred to as the inner product, the dot product can be represented using the notations <v₁,v₂>, (v₁,v₂), or v₁•v₂.

It's important to note that the dot product of two vectors, such as <v₁,v₂>, is a scalar, a single number. This is distinct from the product of a vector and a scalar, k. They are fundamentally different operations.

Why is it Important?

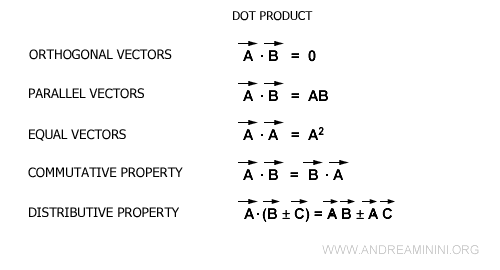
The dot product has several geometric properties:

• When two vectors are orthogonal (perpendicular), their dot product is zero.
  

  
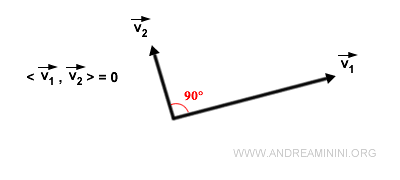
  This is because the cosine of a 90° angle is zero. Thus, a zero dot product indicates that vectors might be orthogonal.

  However, a zero dot product can also occur if one or both vectors are zero vectors. . Some insights from this include:
  
  
  • A vector's dot product with itself is zero only if it's a zero vector: $$ <\vec{v},\vec{v}> = 0 \ \Leftrightarrow \vec{v} = \{ ø \} $$
  • For non-zero vectors, the dot product with itself is the square of its magnitude: $$ <\vec{v},\vec{v}> = |\vec{v}|^2 \ \Leftrightarrow \ \vec{v} \ne \{ ø \} $$
• If two vectors are parallel or coincident, their dot product is the product of their magnitudes. This is because the cosine of a 0° angle is one, making the dot product <v₁,v₂> equivalent to |v₁|·|v₂|.
  
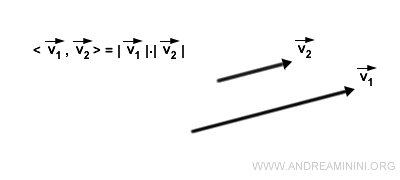
• The dot product can be used to determine a vector's length or the angle between two vectors.

Dot Product Properties. Here's a quick recap of the dot product's key properties.

It's worth noting that the dot product with a zero vector is always zero, given the zero vector's magnitude is zero. Thus, a zero dot product suggests vectors might be orthogonal but doesn't confirm it.

A Hands-on Example with Vectors

Consider two vectors in the two-dimensional space R²

$$ \vec{ v_1} = \begin{pmatrix} 4 \\ 1 \end{pmatrix} $$

$$ \vec{ v_2 } = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Here's a visual representation:

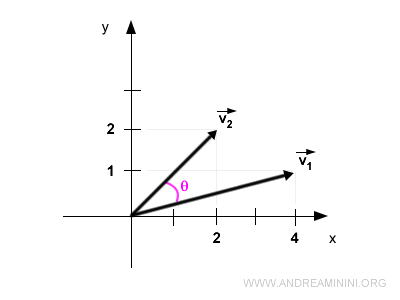
These vectors form an angle of θ = 30,96°.

To determine their dot product:

$$ < \vec{ v_1} , \vec{v_2} > = \vec{v_1} \cdot \vec{v_2} $$

Projecting vector v₂ onto v₁ orthogonally results in a new vector with a magnitude of |v₂|·cos θ aligned with v₁.

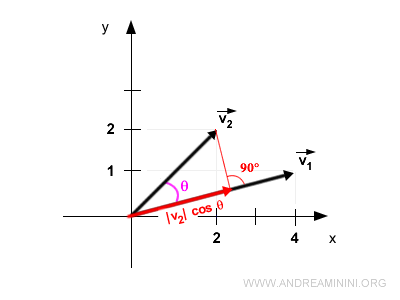
Multiplying the magnitudes of these vectors gives:

$$ < \vec{ v_1} , \vec{v_2} > = |\vec{v_1}| \cdot ( | \vec{v_2}| \cdot \cos \theta) $$

Given the magnitudes |v₁| = 4.12 and |v₂| = 2.83:

$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,83 \cdot \cos \theta) $$

$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,83 \cdot \cos 30,96°) $$

With cos 30.96° = 0.86

$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,83 \cdot 0,86 ) $$

$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot ( 2,43 ) $$

Note. The term 2,83·cos(30,96°) is the magnitude of the projected vector on v₁, equivalent to |v₂|·cos θ.

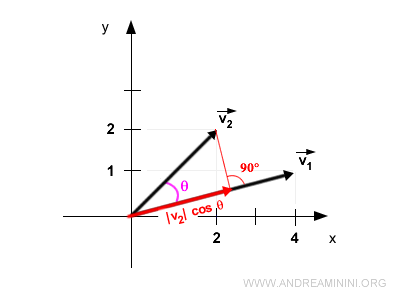
Thus, the dot product is:

$$ < \vec{ v_1} , \vec{v_2} > = 4,12 \cdot 2,43 $$

$$ < \vec{ v_1} , \vec{v_2} > = 10 $$

Note. The dot product is commutative. So, projecting v₁ onto v₂ would yield the same result.

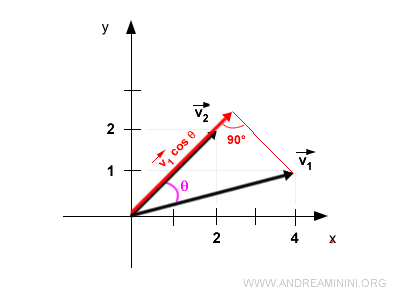
A More Efficient Calculation

For a streamlined approach to the dot product, consider the Euclidean method:

$$ < \vec{ v_1} , \vec{v_2} > = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$

This method is straightforward and quick. Simply multiply corresponding components and sum them.

 

 

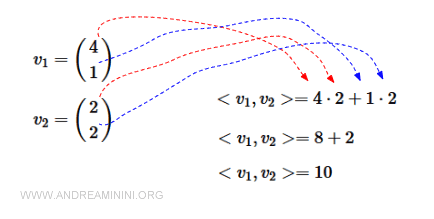
For our vectors, the x-components are 4 and 2, and the y-components are 1 and 2.

This result is consistent with the previous method.

Properties of the Dot Product

The dot product of two vectors, both belonging to the same vector space V over the field K=R, is a symmetric and bilinear function. This means that for vectors v₁ and v₂:

$$ <·,·> \:\: := \:\: VxV \:\: \rightarrow \:\: R $$

Euclidean Dot Product

Among the various definitions of the dot product, the Euclidean dot product is defined as: $$ <v_1 , v_2 > = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$

Example

Consider two vectors v₁ and v₂ in V=R³

$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$

Their Euclidean dot product is:

$$ < v_1 , v_2 > = ( 2·3 ) + ( (-1)·(-1) ) + ( 1·0 ) $$

$$ < v_1 , v_2 > = 6+1+0 $$

$$ < v_1 , v_2 > = 7 $$

Note. The dot product is non-degenerate. If <w,v> = 0 for any vector w in V, then v is the zero vector.

 

Proof of the Dot Product Formula

Given vectors a and v, their dot product is:

$$ \vec{a} \cdot \vec{b} $$

Where:

$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} $$

$$ \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$

Expanding using distributive properties and noting that the dot product between orthogonal unit vectors is zero:

$$ \vec{a} \cdot \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \cdot ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) = $$

$$ a_x \vec{u_x} b_x \vec{u_x} + a_x \vec{u_x} b_y \vec{u_y} + a_x \vec{u_x} b_z \vec{u_z} + $$

$$ a_y \vec{u_y} b_x \vec{u_x} + a_y \vec{u_y} b_y \vec{u_y} + a_y \vec{u_y} b_z \vec{u_z} + $$

$$ a_z \vec{u_z} b_x \vec{u_x} + a_z \vec{u_z} b_y \vec{u_y} + a_z \vec{u_z} b_z \vec{u_z} = $$

Given that the dot product between two orthogonal vectors is zero:

$$ \vec{u_x} \cdot \vec{u_y} = \vec{u_y} \cdot \vec{u_x} = 0 $$ $$ \vec{u_x} \cdot \vec{u_z} = \vec{u_z} \cdot \vec{u_x} = 0 $$ $$ \vec{u_y} \cdot \vec{u_z} = \vec{u_z} \cdot \vec{u_y} = 0 $$

Many terms cancel out:

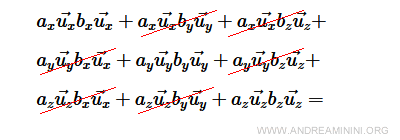
The sum reduces to three terms:

$$ a_x \vec{u_x} b_x \vec{u_x} + a_y \vec{u_y} b_y \vec{u_y} + a_z \vec{u_z} b_z \vec{u_z} = $$

Thus, I can rewrite the dot product in this equivalent form:

$$ a_x b_x \vec{u_x} \vec{u_x} + a_y b_y \vec{u_y} \vec{u_y} + a_z b_z \vec{u_z} \vec{u_z} = $$

The dot product of a vector with itself is equal to the product of its magnitudes, because the cosine of a zero angle is 1.

Nota. $$ v \cdot v = |v||v| \cos 0 = |v|^2 $$

Knowing that the magnitude of the unit vectors is one, the dot products u_xu_x=1, u_yu_y=1, u_zu_z=1.

$$ a_x b_x \cdot ( \vec{u_x} \vec{u_x} ) + a_y b_y \cdot ( \vec{u_y} \vec{u_y} ) + a_z b_z \cdot ( \vec{u_z} \vec{u_z} ) = $$

$$ a_x b_x \cdot (1 ) + a_y b_y \cdot ( 1 ) + a_z b_z \cdot ( 1 ) = $$

$$ a_x b_x + a_y b_y + a_z b_z $$

This proves that the dot product between two vectors is equal to the sum of the products of their components along the x, y, z axes.

$$ \vec{a} \cdot \vec{b} =a_x b_x + a_y b_y + a_z b_z $$

The Norm Induced by the Dot Product

There's a close relationship between the dot product of vectors and the norm (or magnitude) of a vector.

The norm of any vector is equal to the square root of its dot product with itself.

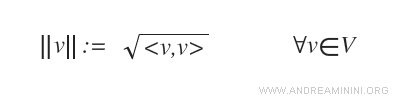
This norm is referred to as the norm induced by the dot product.

Note. The norm represents the length of the vector and is also known as the vector's magnitude.

Example

Consider a vector v₁ in the vector space V=R³ over the field K=R

$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$

The norm of a vector is:

$$ || v_1 || = < v_1 , v_1 > = \sqrt { <v_1 , v_1 > } $$

$$ || v_1 || = < v_1 , v_1 > = \sqrt { ( 2·2 ) + ( (-1)·(-1) ) + ( 1·1 ) } $$

$$ || v_1 || = < v_1 , v_1 > = \sqrt { 4+1+1 } $$

$$ || v_1 || = < v_1 , v_1 > = \sqrt { 6 } $$

Cauchy-Schwarz Inequality

According to the Cauchy-Schwarz inequality:

The absolute value of the dot product of two vectors <v₁,v₂> is less than or equal to the product of their norms, ||v₁||·|| v₂|| , induced by the dot product.

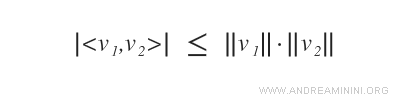
If the dot product of the two vectors v₁ and v₂ equals the product of their norms, then they are linearly dependent.

 

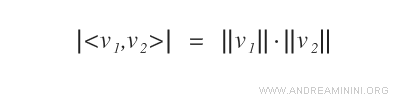
Example

Given two vectors v₁ and v₂ in the vector space V=R³ over the field K=R

$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$

The absolute value of the dot product <v₁,v₂> is

$$ |< v_1 , v_2 >| = | 7 | = 7 $$

The norms of the two vectors are:

$$ || v_1 || = \sqrt { (2*2)+(-1*-1)+(1*1) } = \sqrt {6} $$

$$ || v_2 || = \sqrt { (3*3)+(-1*-1)+(0*0) } = \sqrt {10} $$

According to the Cauchy-Schwarz inequality:

$$ |< v_1 , v_2 >| \le || v_1 || · || v_2 || $$

$$ 7 \le \sqrt {6} · \sqrt {10} $$

$$ 7 \le 7.7459 $$

Thus, based on the inequality, the two vectors are not linearly dependent.

Example 2

Now, let's consider two linearly dependent vectors:

$$ v_1 = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} -1 \\ 1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$

Note. The determinant of the matrix formed by the two vectors is zero, indicating that the vectors are linearly dependent.

The absolute value of the dot product <v₁,v₂> is

$$ |< v_1 , v_2 >| = | (-1·1)+(1·-1) | = 2 $$

The norms of the two vectors are:

$$ || v_1 || = \sqrt { (-1*-1)+(1*1) } = \sqrt {2} $$

$$ || v_2 || = \sqrt { (1*1)+(-1*-1) } = \sqrt {2} $$

According to the Cauchy-Schwarz inequality:

$$ |< v_1 , v_2 >| \le || v_1 || · || v_2 || $$

$$ 2 \le \sqrt {2} · \sqrt {2} $$

$$ 2 = 2 $$

In this case, the two values are equal because the vectors are linearly dependent. This confirms the Cauchy-Schwarz inequality.

Notes

Some useful or interesting notes on the dot product between vectors:

• Unlike the product of real numbers, the dot product between vectors can be zero even if neither vector is zero. For example, if the vectors are perpendicular, their dot product is zero because the cosine of 90° is zero. This means that even though the vectors themselves aren't zero, their dot product is.
• If two vectors have the same direction and sense, the dot product is equal to the product of their magnitudes.
• If two vectors have the same direction but opposite senses, the dot product is equal to the negative product of their magnitudes.