Relationship Between the Dot Product and Vector Length

The dot product of a vector with itself is equal to the square of the vector's magnitude: $$ \vec{v} \cdot \vec{v} = | \vec{v} |^2 $$

This relationship is particularly useful because it allows us to calculate the length (magnitude or norm) of the vector.

To do this, simply take the square root of the dot product of the vector with itself:

$$ | \vec{v} | = \sqrt{ \vec{v} \cdot \vec{v} } $$

A Practical Example

Let's consider a vector:

$$ \vec{v} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

Visually, it looks like this:

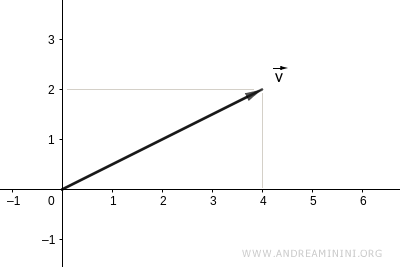
To calculate the vector's magnitude (norm), we first find the dot product of the vector with itself:

$$ \vec{v} \cdot \vec{v} = 2 \cdot 2 + 4 \cdot 4 = 2^2 + 4^2 = 4
+ 16 = 20 $$

Since the dot product of the vector with itself equals the square of its magnitude:

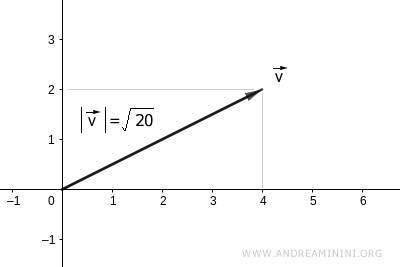
$$ | \vec{v} |^2 = \vec{v} \cdot \vec{v} = 20 $$

We can find the magnitude by taking the square root of the dot product:

$$ | \vec{v} | = \sqrt{ 20 } $$

And this gives us the length of the vector:

Proof

Consider a vector with coordinates (x, y):

$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $$

For simplicity, we'll work with a two-dimensional vector, but the reasoning holds for vectors in any number of dimensions.

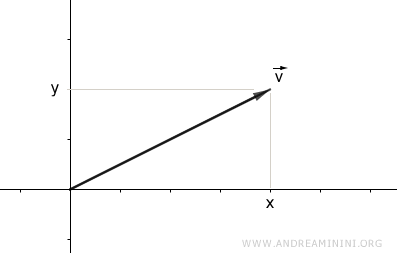
The projection of the vector's coordinates (x, y) onto the Cartesian axes forms a right triangle ABC.

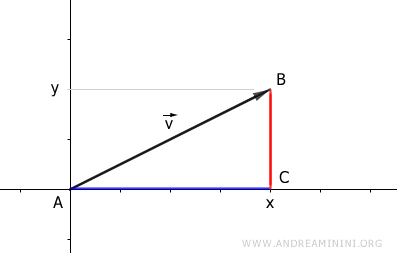
In this triangle, the projections onto the axes are the lengths of the legs, while the vector's length (magnitude) is the hypotenuse.

The dot product of the vector with itself is the sum of the squares of the triangle's sides:

$$ \vec{v} \cdot \vec{v} = x \cdot x + y \cdot y = x^2 + y^2 $$

According to the Pythagorean Theorem, the sum of the squares of the legs is equal to the square of the hypotenuse:

$$ \overline{AB}^2 = \overline{BC}^2 + \overline{AC}^2 $$

In this case, AC = x, BC = y, and AB represents the vector's length (magnitude) |v|:

$$ | \vec{v} |^2 = x^2 + y^2 $$

Thus, the dot product of a vector with itself gives the square of its magnitude:

$$ \vec{v} \cdot \vec{v} = x^2 + y^2 = | \vec{v} |^2 $$

Therefore, the magnitude of the vector is the square root of the dot product:

$$ | \vec{v} | = \sqrt{\vec{v} \cdot \vec{v}} $$

Note: The magnitude of a vector is also known as its norm. The terms "magnitude" and "norm" refer to the same scalar value, which is the vector's length: $$ || \vec{v} || = \sqrt{\vec{v} \cdot \vec{v}} $$

And so on.