Angle Between Two Vectors

To find the angle between two vectors, I employ the formula that leverages the arccosine. It's based on the ratio of the vectors' dot product to the multiplication of their magnitudes. $$ \alpha = \arccos ( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} )$$

This formula holds true regardless of the quadrant in which the vectors lie.

It always returns the smallest angle between the two vectors, ranging from 0° to 180°, regardless of their orientation in the plane.

Example

To illustrate, let me walk you through a practical example:

I'm given two vectors:

$$ \vec{v} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$

$$ \vec{w} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

When I visualize these vectors, they lie on a plane.

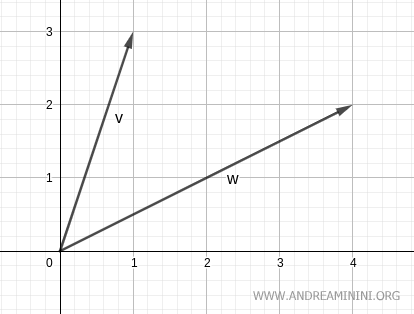
To find the angle between them, I apply the formula:

$$ \alpha = \arccos ( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} )$$

First, I calculate the dot product:

$$ \vec{v} \cdot \vec{w} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ 2 \end{pmatrix} = 1 \cdot 4 + 3 \cdot 2 = 4+6= 10$$

Plugging this into the formula:

$$ \alpha = \arccos ( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} )$$

$$ \alpha = \arccos ( \frac{10}{ |\vec{v}| \cdot |\vec{w}|} )$$

Next, I determine the magnitudes using the Pythagorean theorem.

$$ |\vec{v}| = \sqrt{3^2+1^2} = \sqrt{10} $$

$$ |\vec{w}| = \sqrt{4^2+2^2} = \sqrt{20} $$

Substituting these magnitudes in:

$$ \alpha = \arccos ( \frac{10}{ |\vec{v}| \cdot |\vec{w}|} )$$

$$ \alpha = \arccos ( \frac{10}{ \sqrt{10} \cdot \sqrt{20}} )$$

$$ \alpha = \arccos ( \frac{10}{ \sqrt{200} } )$$

$$ \alpha = \arccos ( 0,71 )$$

From this, I deduce:

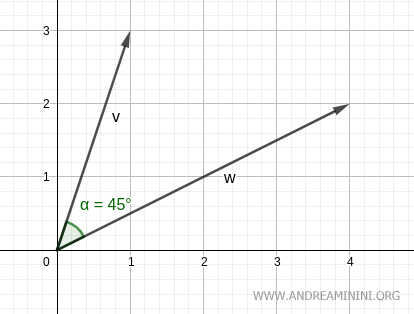
$$ \alpha = 45° $$

So, the angle between these two vectors is 45°.

Example 2

Let’s now consider two vectors located in different quadrants:

$$ \vec{v} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} \quad \text{(first quadrant)} $$

$$ \vec{w} = \begin{pmatrix} -1 \\ 3 \end{pmatrix} \quad \text{(second quadrant)} $$

Their dot product is:

$$ \vec{v} \cdot \vec{w} = 2 \cdot (-1) + 1 \cdot 3 = -2 + 3 = 1 $$

The magnitudes are:

$$ |\vec{v}| = \sqrt{2^2 + 1^2} = \sqrt{5} $$

$$ |\vec{w}| = \sqrt{(-1)^2 + 3^2} = \sqrt{10} $$

So the angle between the vectors is:

$$ \alpha = \arccos \left( \frac{1}{\sqrt{5} \cdot \sqrt{10}} \right) = \arccos \left( \frac{1}{\sqrt{50}} \right) \approx \arccos(0.141) \approx 81.87^\circ $$

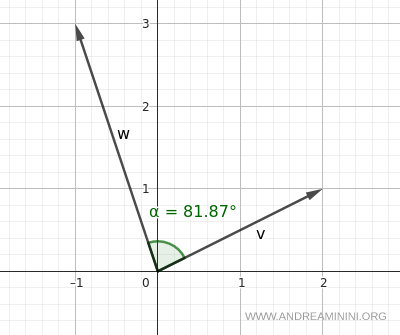
The resulting angle is approximately 81.87°:

$$ \alpha \approx 81.87^\circ $$

Although the vectors are in different quadrants - affecting the signs of their components - the formula still yields the correct (unsigned) angle between them, always within the range of 0° to 180°. Since it’s not a directed angle, it cannot be 270°.

Proof

For those interested in the underlying proof.

The dot product of two vectors is the product of their magnitudes and the cosine of the angle between them.

$$ \vec{v} \cdot \vec{w} = |\vec{v}| \cdot |\vec{w}| \cdot \cos \alpha $$

From this relationship, I can isolate the cosine of angle α.

$$ \cos \alpha = \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } $$

Taking the arccosine of both sides.

$$ \arccos( \cos \alpha ) = \arccos( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } ) $$

Since the arccosine is the inverse function of cosine, the arccosine of the cosine of α gives me angle α.

$$ \alpha = \arccos( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } ) $$

This confirms the formula I use to calculate the angle between two vectors.