Vector Field
What is a vector field?
A vector field is a function F that assigns a vector to each point in space. $$ \vec{v} = F(x,y,z) $$
In other words, at every point in three-dimensional space (xyz), three scalar quantities are assigned that describe how much the vector points along the x-, y-, and z-axes.
In two-dimensional space (xy), each point is instead associated with two scalar quantities - these are the components of the vector along the x- and y-axes.
Are the vectors the same at every point, or do they vary?
In a vector field, the vectors may vary in direction, orientation, and magnitude - or they may be uniform throughout the field.
Here is a practical example of a vector field defined over a region of the plane (two-dimensional space):
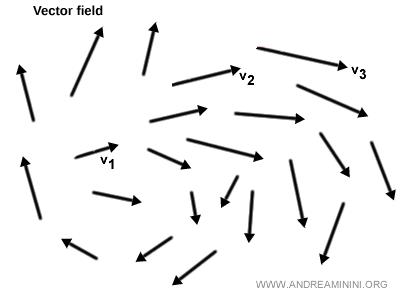
Example. The wind displayed on a weather map. Each point on the map is represented by an arrow indicating both the direction from which the wind is blowing and its strength. This is an example of a vector field.
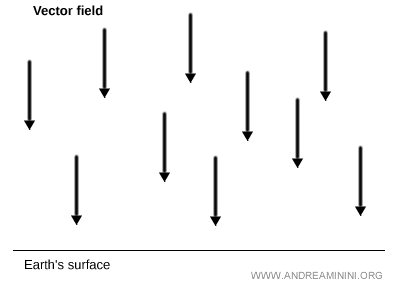
If all the vectors are identical, the field is referred to as a constant vector field.
One example is the gravitational force near the Earth's surface.
A vector field can also be defined in three-dimensional Euclidean space.
For example, consider the direction, orientation, and intensity of airflow around a sphere:
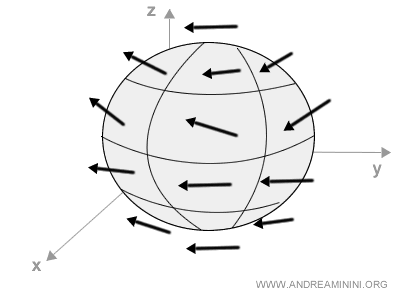
In this case, each vector has three components representing its projections onto the x-, y-, and z-axes:
$\vec{v}(x, y, z) = \begin{pmatrix} v_x(x,y,z) \\ v_y(x,y,z) \\ v_z(x,y,z) \end{pmatrix}$
More generally, a vector field may also vary over time - in this case, a fourth variable representing time is introduced: $ F(x, y, z, t) $.
A practical example
Consider the following vector field:
$\vec{v}(x,y,z) = (2x,\ -y,\ 3z)$
What are the scalar components of the vector at the point $(1,2,3)$?
The coordinates of the point in space are:
$$(x_0, y_0, z_0) = (1,2,3)$$
We substitute these coordinates into the function that defines the vector field:
$$ \vec{v}(1,2,3) = (2 \cdot 1,\ -2,\ 3 \cdot 3)$$
$$ \vec{v}(1,2,3) = (2, -2, 9)$$
The components of the vector - that is, the scalar values that describe the vector at point $(1,2,3)$ - are:
$$v_x = 2 $$
$$ v_y = -2 $$
$$ v_z = 9 $$
Thus:
$\vec{v}(1,2,3) = (2,\ -2,\ 9)$
This means that at point $ (1,2,3) $, the vector has a component of $ +2 $ along the x-axis, $ -2 $ along the y-axis, and $ +9 $ along the z-axis.
Graphically, the vector can be represented as an arrow originating at point $ (1,2,3) $ and pointing toward point $ (3,0,12) $, which corresponds to the sum of the point’s coordinates and the components of the vector:
$$ (1,2,3)+(2,-2,9)=(1+2, 2-2, 3+9) = (3,0,12) $$
Here is how this appears in 3D space:
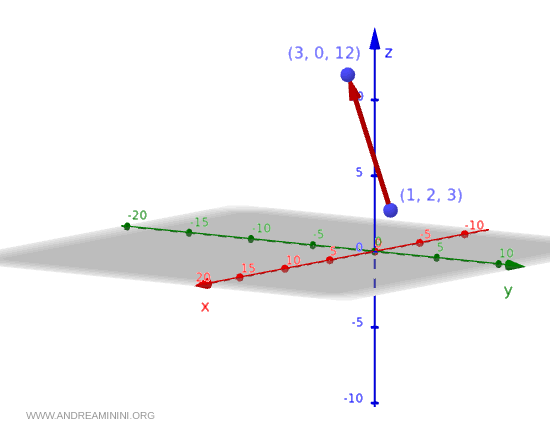
The same computation can be performed for every point within the domain of the vector field:
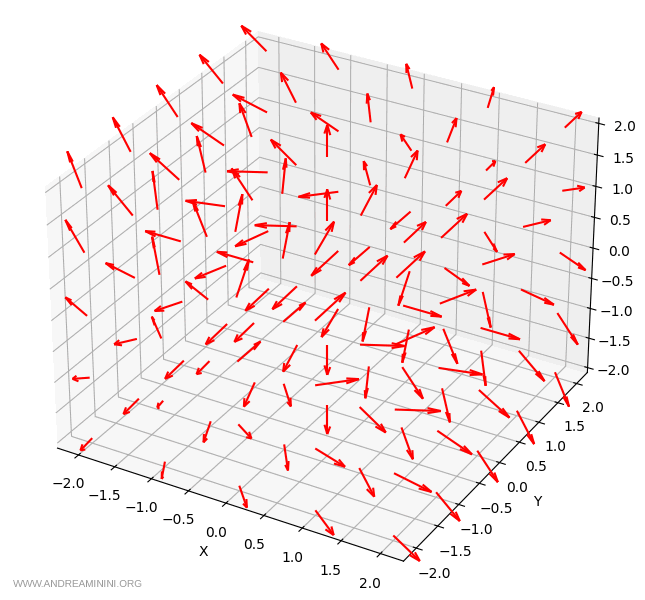
Note. In the final visualization, the vectors have been normalized - that is, they are displayed with the same graphical length to improve readability. The directions are correct, but the drawn length does not represent the actual magnitude of each vector.
Difference Between a Vector Field and a Vector Space
Confusing vector fields with vector spaces is a common pitfall for those new to the subject.
Despite the similar names, they refer to two fundamentally different concepts.
- Vector Space
A vector space (or linear space) is a set of elements, called "vectors", that can be added together and scaled by numbers (scalars) from a field such as ℝ or ℂ, and that satisfy a specific set of axioms. These vectors aren't limited to geometric arrows - they can be functions, matrices, or other mathematical objects. A vector space is an abstract algebraic structure, defined by the operations it supports. - Vector Field
In mathematics, a vector field is a function that assigns a vector to each point in a space - typically in ℝ² or ℝ³. In physics, however, a vector field may refer more broadly to any mapping that associates a vector with every point in a region, even without an explicit global formula. A common example is a weather map showing wind direction and magnitude at different locations.
And so on.
