Cross Product

Understanding the Vector Cross Product in Space

The vector cross product is a unique multiplication between two vectors that yields a third vector. When we say "vector u cross vector v", we denote it as: . $$ \vec{u} \ × \ \vec{v} = \vec{w} $$ Alternatively, it can be expressed as: $$ \vec{u} \ ∧ \ \vec{v} = \vec{w} $$The magnitude of this cross product is represented by: $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$

This operation takes place between two vectors in the Euclidean space R³, producing a third vector as its result.

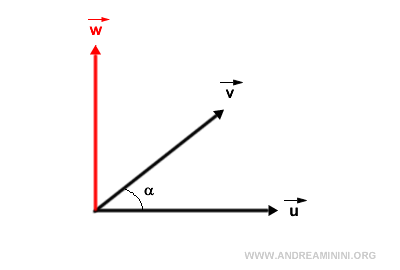
The resulting vector w from the cross product is orthogonal to the initial two vectors, meaning it stands perpendicular to both.

The cross product operation is commonly symbolized by the "×" sign, but can also be represented by the "∧" symbol.

Properties of the Vector Cross Product. It's essential to familiarize oneself with the core properties of the vector cross product, as they form the foundation of vector mathematics.

Geometric Properties of the Cross Product

The vector w derived from the cross product exhibits the following characteristics:

• The magnitude of the cross product (vector w) corresponds to the area of the parallelogram spanned by vectors u and v.
  
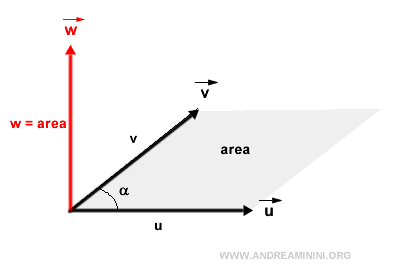
  Trigonometrically, the magnitude of vector w is given by the product of the magnitudes of vectors u and v, multiplied by the sine of the angle α_uv between them. Mathematically: $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$ This can be thought of as the product of vector u and the projection of vector v onto u.

  Note. Some insightful properties of the cross product emerge from this. When two vectors are collinear, their cross product is zero, given the null area they span. Thus, if the vectors form angles of 180° (antiparallel) or 0° (parallel), their cross product is a null vector.
  
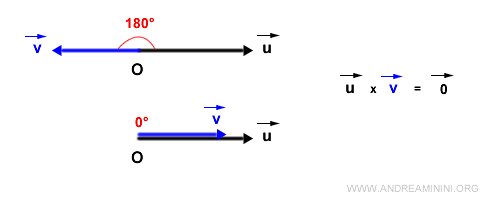
  For orthogonal vectors (forming a 90° angle), the magnitude of the cross product is simply the product of their magnitudes, as the sine of 90° is 1.
  
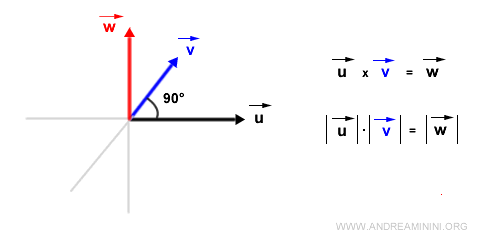
  If the vectors form an angle of -90°, the magnitude of the cross product remains the product of their magnitudes but with an inverted direction, since the sine of -90° is -1. Thus, the cross product's direction is opposite to the previous case.
  

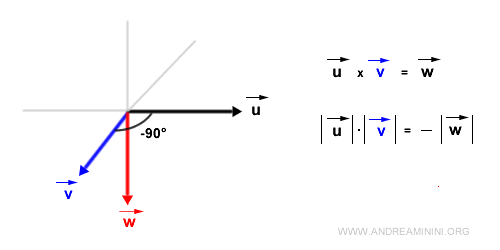
• The direction of the cross product, denoted as vector w, is perpendicular to the plane defined by vectors u and v.
  
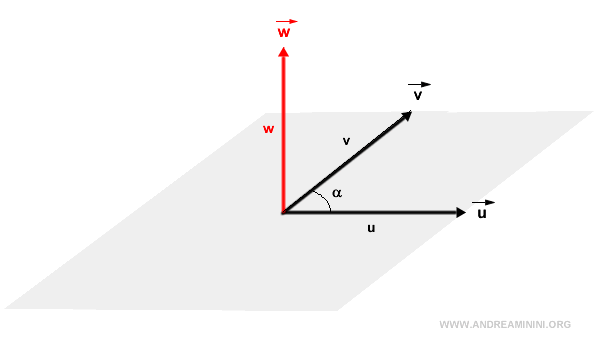
• To determine the orientation of the cross product w, one can employ the right-hand rule. Here, the thumb corresponds to vector u, the index finger represents vector v, and the middle finger points in the direction of vector w.
  
  

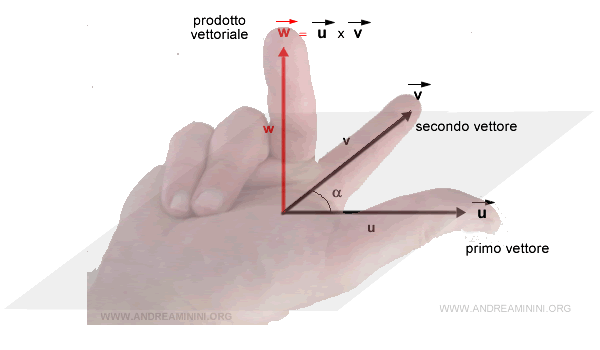
  Note. Ensure that the thumb always aligns with the first vector in the cross product, and the index finger with the second.

  Alternative Approach for Determining Direction
  First, identify the plane that encompasses both vectors. Observing from a top-down perspective, if the most direct rotation to align vector u with vector v is counterclockwise, then the cross product w=u×v points upwards. This principle is commonly known as the right-hand screw rule.
  
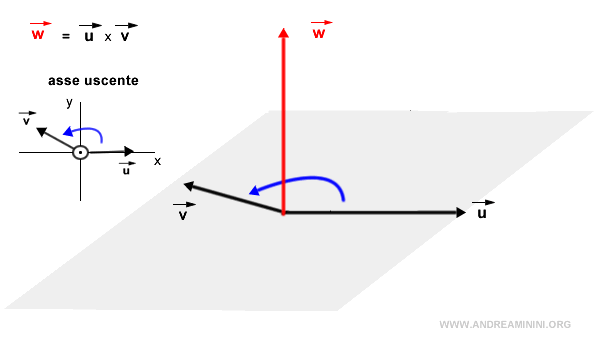
  Conversely, if the most direct rotation to align vector u with vector v is in a clockwise direction, then the cross product w=u×v points downward, opposite to the plane in reference to the observer.
  
  

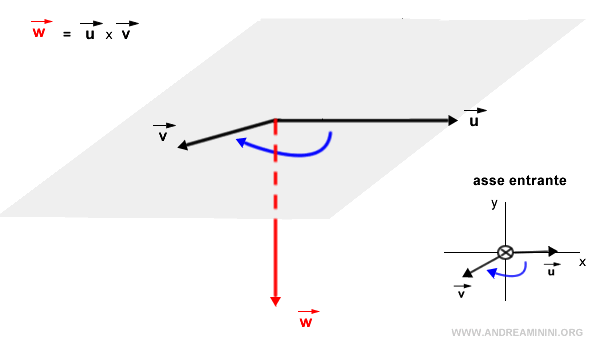
  Note. In general, when observing from the tip of the cross product vector w=u×v and looking down onto the plane, the most direct rotation to align vector u with vector v is consistently counterclockwise.

Computing the Cross Product

To determine the cross product, you can employ two distinct methods.

Method 1:

Given vectors:

$$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$

and

$$ \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} $$

Their cross product is:

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} det \begin{pmatrix} y_1 & y_2 \\ z_1 & z_2 \end{pmatrix} \\ - det \begin{pmatrix} x_1 & x_2 \\ z_1 & z_2 \end{pmatrix} \\ det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \end{pmatrix} $$

Method 2:

The cross product can also be expressed as:

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = det \begin{pmatrix} i & x_1 & x_2 \\ j & y_1 & y_2 \\ k & z_1 & z_2 \end{pmatrix} $$

A Hands-on Example

In the three-dimensional space R³, consider the following vectors:

$$ \vec{v_1} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Let's determine the cross product v₁ × v₂ using two distinct methods.

Method 1

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} det \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} \\ - det \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} \\ det \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} \end{pmatrix} $$

This results in:

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \cdot 2 - (-3) \cdot 1 \\ - ( 1 \cdot 2 - 1 \cdot 1 ) \\ 1 \cdot (-3) - 1 \cdot 2 \end{pmatrix} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix}$$

This yields a vector orthogonal to our original pair, forming a 90° angle with both.

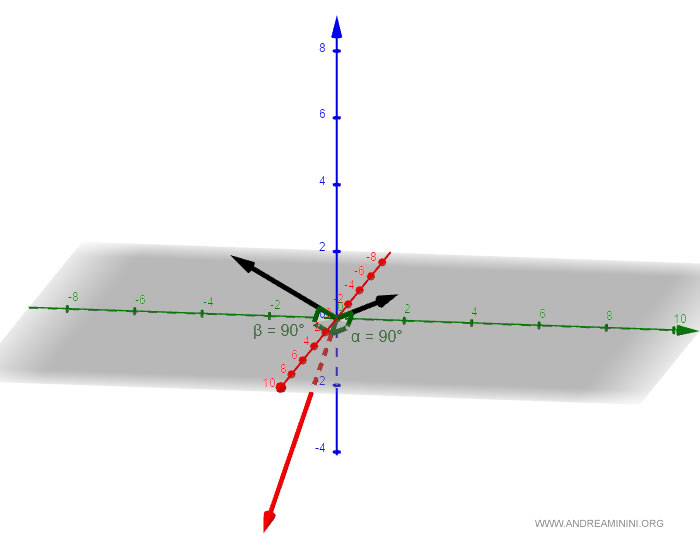
The dot product of two orthogonal vectors is zero. $$ < \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} > = 7 \cdot 1 + (-1) \cdot 2 + (-5) \cdot 1 = 7 -2 -5 = 0 $$ $$ < \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} > = 7 \cdot 1 + (-1) \cdot (-3) + (-5) \cdot 2 = 7 +3 -10 = 0 $$ This verifies that our new vector is indeed orthogonal to the initial ones.

Method 2

Starting with:

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = det \begin{pmatrix} i & 1 & 1 \\ j & 2 & -3 \\ k & 1 & 2 \end{pmatrix} $$

We can expand this to:

$$ \vec{v_1} ∧ \vec{v_2} = i \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} - j \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} + k \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} $$

$$ \vec{v_1} ∧ \vec{v_2} = 7i -j -5k $$

The coefficients of the unit vectors i, j, and k represent the cross product of our two vectors:

$$ \vec{v_1} ∧ \vec{v_2} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix}$$

This result aligns perfectly with Method 1.

Properties of the Cross Product

The cross product, denoted as a×b, possesses several key properties:

Anticommutativity
This implies that the cross product is not commutative. $$ \vec{a} ∧ \vec{b} = -\vec{b} ∧ \vec{a} $$
Distributivity Over Vector Addition
$$ \vec{a} ∧ (\vec{b} + \vec{c} ) = (\vec{a} ∧ \vec{b} ) + ( \vec{a} ∧ \vec{c} ) $$

Other Properties of the Cross Product

$$ k \cdot \vec{a} ∧ \vec{b} = \vec{a} ∧ k \cdot \vec{b} = k \cdot ( \vec{a} ∧ \vec{b} ) $$ $$ < \vec{a} , \vec{a} ∧ \vec{b} > = < \vec{b} , \vec{a} ∧ \vec{b} > = 0 $$ $$ || \vec{a} ∧ \vec{b} ||^2 = || \vec{a} ||^2 \cdot || \vec{b} ||^2 - < \vec{a} , \vec{b} >^2 $$ $$ || \vec{a} ∧ \vec{b} || = || \vec{a} || \cdot || \vec{b} || \cdot sin(\widehat{ \vec{a} , \vec{b} }) $$

To the aforementioned properties, we can add another that's particularly useful for determining if vectors are parallel.

Two vectors are linearly dependent if their cross product is zero: $$ \vec{a} ∧ \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

The cross product is zero under the following circumstances:

• At least one of the vectors is a zero vector: $$ \vec{a} ∧ \vec{b} = 0 \ \ se \ \ \ \vec{a} = \vec{0} \ \ e/o \ \ \vec{b} = \vec{0} $$
• The two vectors are parallel or identical, meaning they're linearly dependent: $$ \vec{a} ∧ \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

Thus, if neither of the vectors is a zero vector, a cross product equal to zero indicates the vectors are linearly dependent, meaning they are parallel or identical.

The cross product does not satisfy the associative property. Associativity isn't upheld by the cross product. Hence, the order in which cross products are taken is crucial: $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) \ne ( \vec{a} \: ∧ \: \vec{b} ) \: ∧ \: \vec{c} $$

 

The Triple Cross Product

The triple cross product is a unique vector operation where one of the factors is itself a cross product, denoted as a × ( b × c ) $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) $$

This operation is bracketed because the cross product isn't associative, meaning:

$$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) \ne ( \vec{a} \: ∧ \: \vec{b} ) \: ∧ \: \vec{c} $$

The triple cross product can be expressed using Lagrange's formula: $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) = ( \vec{a} · \vec{c} ) · \vec{b} - ( \vec{a} · \vec{b} ) · \vec{c} $$ Alternatively, it can be represented as: $$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) = \vec{b} · ( \vec{a} · \vec{c} ) - \vec{c} · ( \vec{a} · \vec{b} ) $$ While the left side of these equations involves cross products, the right side uses dot products. However, the resulting identity is always a vector. A handy mnemonic to remember this is ACB-ABC or BAC-CAB.

 

Example

Consider three vectors:

$$ \vec{a}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$

$$ \vec{b}=\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix} $$

$$ \vec{c}=\begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} $$

To compute the triple cross product ax(bxc), start with the inner cross product:

$$ \vec{a} \: ∧ \: ( \vec{b} \: ∧ \: \vec{c} ) $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \: ∧ \: (\begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix} \: ∧ \: \begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} ) $$

This results in:

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \: ∧ \: \begin{pmatrix} det \begin{pmatrix} 4 & 7\\ 5 & 8 \end{pmatrix} \\ -det \begin{pmatrix} 3 & 6\\ 5 & 8 \end{pmatrix} \\ det \begin{pmatrix} 3 & 6\\ 4 & 7 \end{pmatrix} \end{pmatrix} $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \: ∧ \: \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix} $$

Finally, evaluating the outer cross product gives:

$$ \begin{pmatrix} det \begin{pmatrix} 2 & 6\\ 3 & -3 \end{pmatrix} \\ -det \begin{pmatrix} 1 & -3\\ 3 & -3 \end{pmatrix} \\ det \begin{pmatrix} 1 & -3\\ 2 & 6 \end{pmatrix} \end{pmatrix} $$

$$ \begin{pmatrix} -24 \\ -6 \\ 12 \end{pmatrix} $$

The Cross Product of Cartesian Axes

The cross product between the Cartesian axes is defined as:

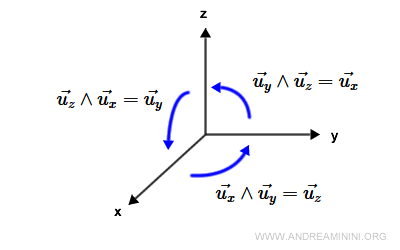
Considering also the opposite unit vectors:

$$ \vec{u_x} ∧ \vec{u_y} = \vec{u_z} $$

$$ \vec{u_y} ∧ \vec{u_x} = - \vec{u_z} $$

$$ \vec{u_y} ∧ \vec{u_z} = \vec{u_x} $$

$$ \vec{u_z} ∧ \vec{u_y} = - \vec{u_x} $$

$$ \vec{u_z} ∧ \vec{u_x} = \vec{u_y} $$

$$ \vec{u_x} ∧ \vec{u_z} = - \vec{u_y} $$

Notably, the cross product of a unit vector with itself is always zero.

$$ \vec{u_x} ∧ \vec{u_x} = \vec{0} $$

$$ \vec{u_y} ∧ \vec{u_y} = \vec{0} $$

$$ \vec{u_z} ∧ \vec{u_z} = \vec{0} $$

Alternative Formula for the Cross Product

In R³ space, the cross product of two vectors can be expressed as: $$ \vec{a} ∧ \vec{b} = (a_y b_z - a_z b_y ) \vec{u_x} + (a_z b_x - a_x b_z) \vec{u_y} + ( a_x b_y - a_y b_x ) \vec{u_z} $$

This formula is especially useful when working with vector components.

E' particolarmente utile quando voglio calcolare il prodotto vettoriale usando le componenti dei vettori.

How to remember this formula? Admittedly, it's not the easiest formula to recall. Thankfully, there's a neat trick to quickly derive it. Set up a table with the unit vectors (u) in the first row, the first vector (a) in the second row, and the second vector (b) in the third row: $$ \begin{pmatrix} u_x & u_y & u_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{pmatrix} $$ Now, treat it as a matrix and compute the determinant using Sarrus' rule: $$ u_x a_y b_z + u_y a_z b_x + u_z a_x b_y - u_z a_y b_x - u_x a_z b_y - u_y a_x b_z $$ Then, factor out the unit vectors: $$ (a_y b_z - a_z b_y )u_x + ( a_z b_x - a_x b_z )u_y + (a_x b_y - a_y b_x )u_z $$

Proof of the Formula

Consider a cross product between two vectors in R³ space:

$$ \vec{a} ∧ \vec{b} $$

A vector is the sum of its x, y, z components:

$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} $$

$$ \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$

Thus, the cross product can be equivalently written as:

$$ \vec{a} ∧ \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) $$

By the Distributive Property over Addition

$$ a_x \vec{u_x} \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) + a_y \vec{u_y} \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) + a_z \vec{u_z} \ ∧ \ ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) = $$

Further, by the Distributive Property over Addition

$$ a_x \vec{u_x} \ ∧ \ b_x \vec{u_x} + a_x \vec{u_x} \ ∧ \ b_y \vec{u_y} + a_x \vec{u_x} \ ∧ \ b_z \vec{u_z} + $$

$$ a_y \vec{u_y} \ ∧ \ b_x \vec{u_x} + a_y \vec{u_y} \ ∧ \ b_y \vec{u_y} + a_y \vec{u_y} \ ∧ \ b_z \vec{u_z} + $$

$$ a_z \vec{u_z} \ ∧ \ b_x \vec{u_x} + a_z \vec{u_z} \ ∧ \ b_y \vec{u_y} + a_z \vec{u_z} \ ∧ \ b_z \vec{u_z} = $$

Given that the cross product between u_x ∧ u_x = 0, u_y ∧ u_y = 0, u_z ∧ u_z = 0.

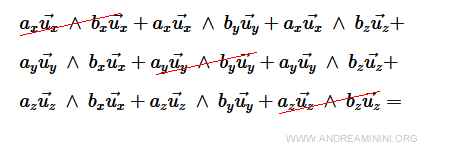
After simplifying, the equation becomes:

$$ a_x \vec{u_x} \ ∧ \ b_y \vec{u_y} + a_x \vec{u_x} \ ∧ \ b_z \vec{u_z} + $$

$$ a_y \vec{u_y} \ ∧ \ b_x \vec{u_x} + a_y \vec{u_y} \ ∧ \ b_z \vec{u_z} + $$

$$ a_z \vec{u_z} \ ∧ \ b_x \vec{u_x} + a_z \vec{u_z} \ ∧ \ b_y \vec{u_y} = $$

his can be equivalently written, considering that a_x, a_y, a_z, b_x, b_y, b_z are scalars:

$$ a_x b_y ( \vec{u_x} \ ∧ \ \vec{u_y} ) + a_x b_z ( \vec{u_x} \ ∧ \ \vec{u_z} ) + $$

$$ a_y b_x ( \vec{u_y} \ ∧ \ \vec{u_x} ) + a_y b_z ( \vec{u_y} \ ∧ \ \vec{u_z} ) + $$

$$ a_z b_x ( \vec{u_z} \ ∧ \ \vec{u_x} ) + a_z b_y ( \vec{u_z} \ ∧ \ \vec{u_y} ) = $$

Given that u_x ∧ u_y = u_z and u_y ∧ u_x = -u_z

$$ a_x b_y ( \vec{u_z} ) + a_x b_z ( \vec{u_x} \ ∧ \ \vec{u_z} ) + $$

$$ a_y b_x ( - \vec{u_z} ) + a_y b_z ( \vec{u_y} \ ∧ \ \vec{u_z} ) + $$

$$ a_z b_x ( \vec{u_z} \ ∧ \ \vec{u_x} ) + a_z b_y ( \vec{u_z} \ ∧ \ \vec{u_y} ) = $$

Giving that u_y ∧ u_z = u_x e u_z ∧ u_y = -u_x

$$ a_x b_y ( \vec{u_z} ) + a_x b_z ( \vec{u_x} \ ∧ \ \vec{u_z} ) + $$

$$ a_y b_x ( - \vec{u_z} ) + a_y b_z ( \vec{u_x} ) + $$

$$ a_z b_x ( \vec{u_z} \ ∧ \ \vec{u_x} ) + a_z b_y (- \vec{u_x} ) = $$

Giving that u_z ∧ u_x = u_y e u_x ∧ u_z = -u_y

$$ a_x b_y ( \vec{u_z} ) + a_x b_z ( - \vec{u_y} ) + $$

$$ a_y b_x ( - \vec{u_z} ) + a_y b_z ( \vec{u_x} ) + $$

$$ a_z b_x ( \vec{u_y} ) + a_z b_y (- \vec{u_x} ) = $$

Factoring out the unit vectors:

$$ a_x b_y \vec{u_z} - a_x b_z \vec{u_y} - a_y b_x \vec{u_z} + a_y b_z \vec{u_x} + a_z b_x \vec{u_y} - a_z b_y \vec{u_x} = $$

$$ (a_y b_z - a_z b_y ) \vec{u_x} + ( a_z b_x - a_x b_z ) \vec{u_y} + ( a_x b_y - a_y b_x ) \vec{u_z} $$

This proves the formula.