Adding Two Vectors

When working with two vectors, say v and w, their combined sum v+w can be ascertained in a couple of ways. One common approach is the parallelogram method. Alternatively, one might opt for the algebraic addition of the vectors' individual coordinates. To put it mathematically: $$ \vec{v} + \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} + \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 + w_1 \\ v_2 + w_2 \\ \vdots \\ v_n + w_n \end{pmatrix} $$

Regardless of the method chosen, the outcome remains consistent: the addition of v and w yields another vector.

This resulting entity is aptly termed the 'sum vector'.

The Parallelogram Method

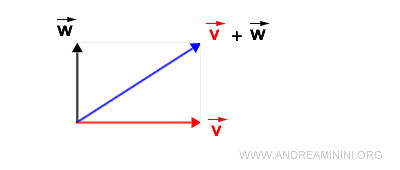
When working with vectors on a plane, the parallelogram method offers a geometric approach to their addition.

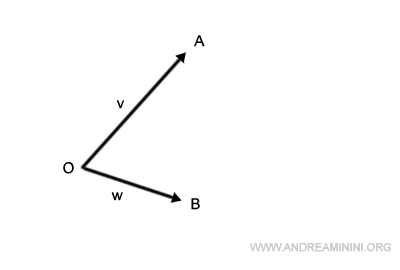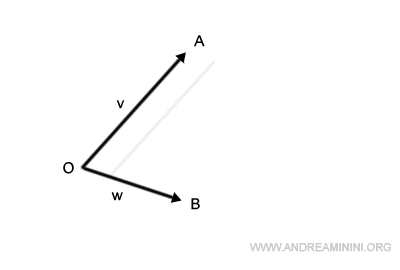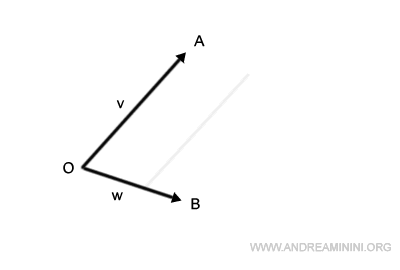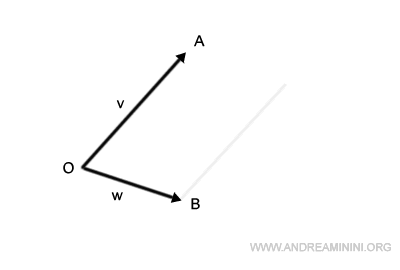
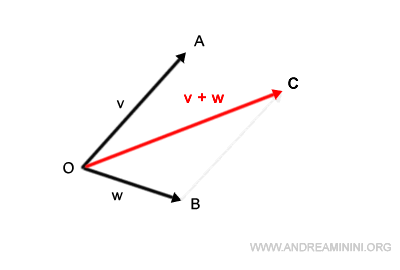
Consider two vectors, v and w. Both originate from a common point, O, but diverge in different directions.

• Vector v extends from point O to point A, representing its magnitude.
• Similarly, vector w stretches from point O to point B.

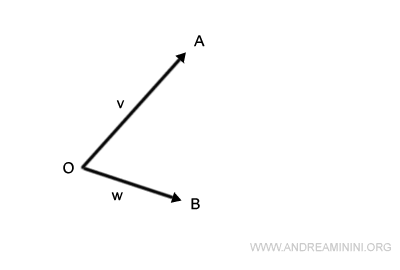
So, how do we determine the sum of these vectors?

First, reposition the segment OA so it emanates from point B.

In a similar fashion, shift the segment OB to begin at point A.

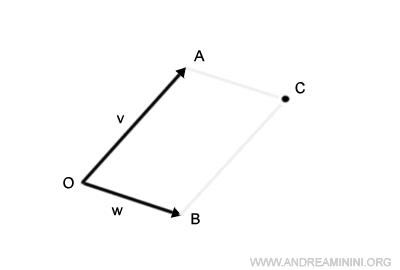
Where these shifted segments intersect, we find point C.

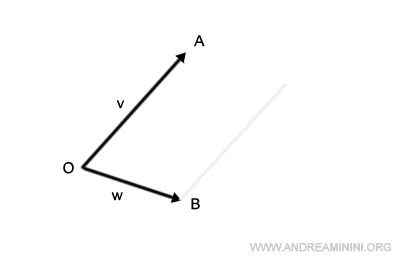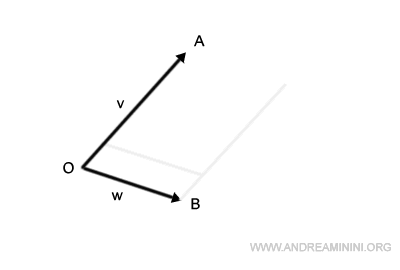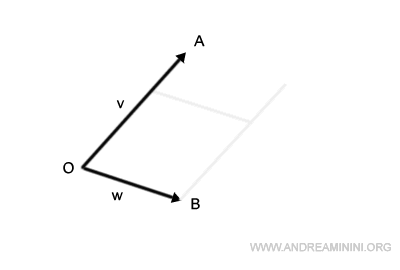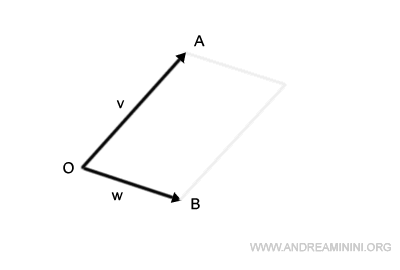
This forms our parallelogram, labeled OACB.

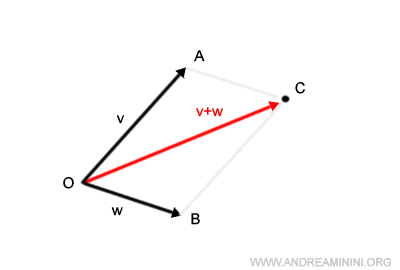
The segment that bridges the origin, O, to point C embodies the sum of our vectors, v+w.

Should two vectors share the same directional path, their lengths will align on a singular straight line. In such cases, the parallelogram method falls short, as it results in a degenerate shape. Instead, professionals often turn to the midpoint method for a solution.

Vector Calculation: An Illustration

In the vector space V=R², I'm working with two distinct vectors:

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

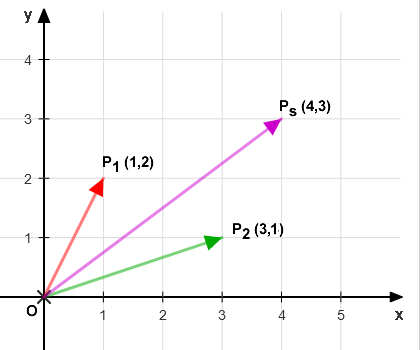
I've graphically represented these on a two-dimensional (x,y) plane. They're depicted as directed line segments: OP₁ and OP₂, which extend from the origin to points P₁ and P₂, respectively.

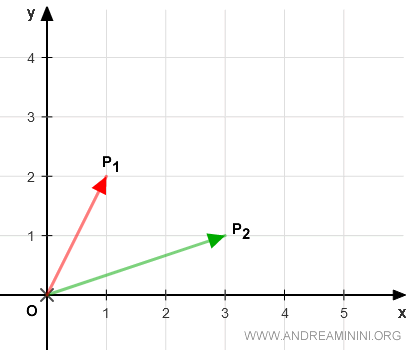
It's essential to understand that every point on our plane can be associated with a vector that originates from the origin. Conversely, each vector that begins at the origin O can be mapped to a specific point on the (x,y) plane. In essence, the points and vectors are two sides of the same coin.

To determine the sum of vectors OP1 and OP₂, I've employed the parallelogram method.

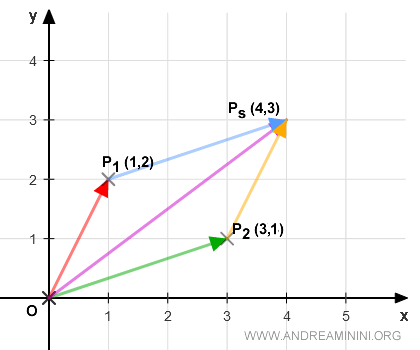
The resulting vector, OP₁+OP₂, seamlessly links the origin to the point P_s(4,3).

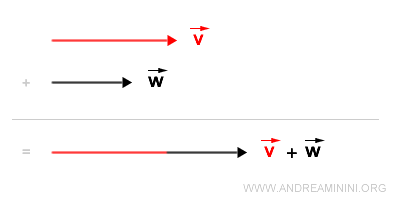
The Tip-to-Tail Method

When working with vectors, there's an intuitive approach I often employ: the tip-to-tail method. Instead of getting bogged down in complex calculations, I can simply shift one vector, aligning its starting point (or base) with the endpoint (or tip) of another.

By adopting this method, I effortlessly pinpoint the coordinates of the resultant vector, v+w.

A Practical Example:

Suppose I'm tasked with finding the sum of vectors v and w. Here's my approach:

I align the base of vector v with the tip of vector w.

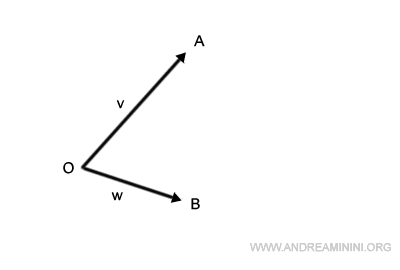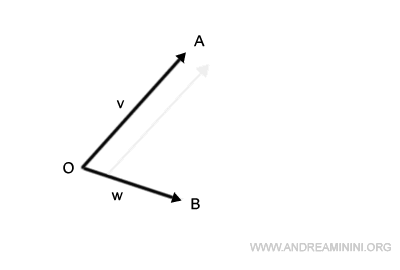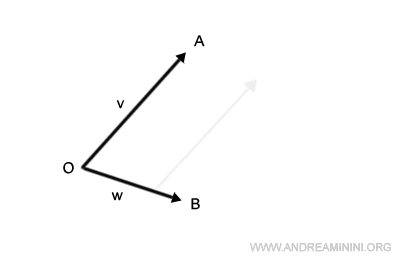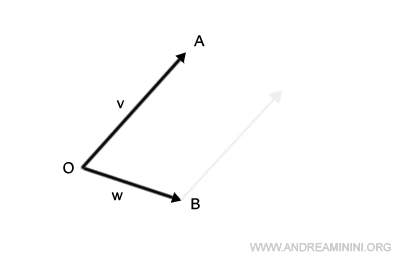
Drawing a line from our origin, O, to the endpoint of the shifted vector v, I unveil the resultant vector v+w.

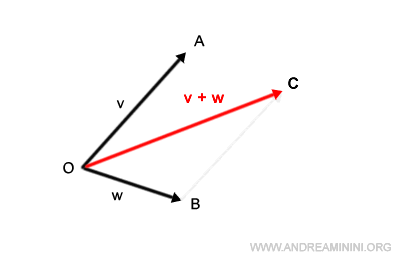
Interestingly, this method yields the same result as the more traditional parallelogram method. Y

et, the tip-to-tail approach is notably more streamlined, and it offers the flexibility to recursively add multiple vectors.

Another Illustration:

Consider the challenge of summing three vectors: v, w, and z.

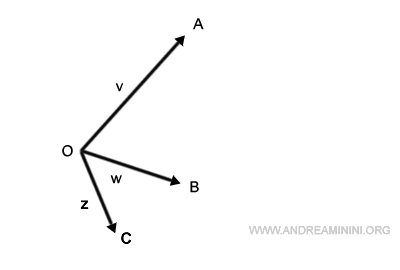
I start by shifting the base of vector w to align with the tip of vector v.

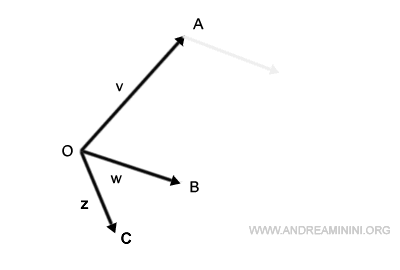
Next, I position the base of vector z to follow the newly positioned vector w.

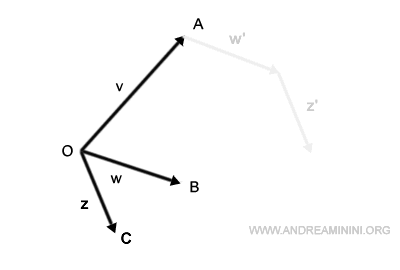
Connecting our origin to the final point, I derive the resultant vector v+w+z.

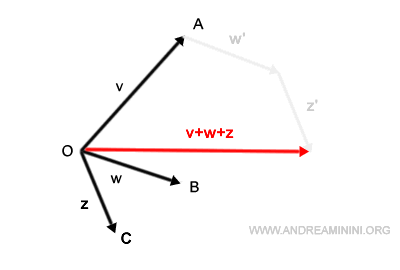
This technique is invaluable for geometrically summing several vectors. And here's a key insight: the sequence in which I arrange these vectors is inconsequential. The final sum remains consistent.

For instance, even if I were to first align vector v with w, and then follow with vector z, the resultant vector v+w+z would remain unchanged. The beauty of this method is that the sum isn't dictated by the order of alignment.

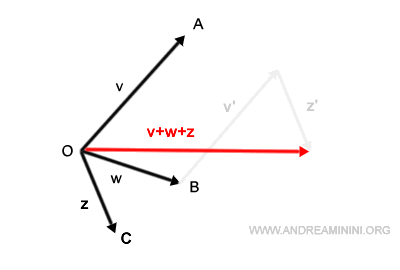
The Algebraic Sum of Vectors

When determining the resultant vector, one can straightforwardly add the (x,y) coordinates of the two vectors. $$ \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix} $$

This algebraic method proves invaluable, especially when dealing with vectors that extend beyond two components.

Example

Revisiting the vectors from our prior discussion:

$$ P_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

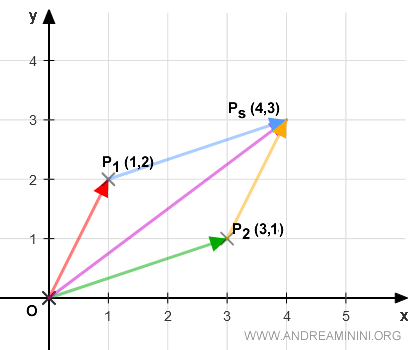
I then compute the algebraic sum of vectors OP₁ and OP₂.

To achieve this, I simply sum the x and y coordinates of both vectors.

$$ OP_S = OP_1 + OP_2 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$

The outcome? Our resultant vector.

I'll now plot this new vector on a Cartesian plane. Interestingly, this vector sum yields a third vector, OP_s.

The point P_s aligns with the resultant vector I derived using the parallelogram method, underscoring the consistency of our approach.

Example 2

Consider two vectors in a three-dimensional space (x, y, z):

$$ P_1= \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix}$$

The resultant vector is derived by summing the x, y, z components:

$$ P_1 + P_2 = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \\ z_1 + z_2 \end{pmatrix} = \begin{pmatrix} 1 + 3 \\ 2 + 1 \\ 3 + 4 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \end{pmatrix} $$

This technique is versatile, applicable to vectors across any dimension.

Example 3

Now, let's delve into vectors within a four-dimensional space (x₁, x₂, x₃, x₄)

$$ v = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ w = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$

The resultant vector is ascertained by summing the components:

$$ v + w = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 \\ 2+1 \\ 3+4 \\ 4+(-2) \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \\ 2 \end{pmatrix} $$

This methodology can be extended to encompass the addition of three or even more vectors.

Example 4

For instance, consider three vectors in a four-dimensional space (x₁, x₂, x₃, x₄)

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$ $$ v_3 = \begin{pmatrix} -1 \\ 1 \\ 1 \\ 3 \end{pmatrix} $$

The resultant vector is formed by aggregating the components:

$$ v_1 + v_2 + v_3 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ 3 \end{pmatrix} + \begin{pmatrix} -1 \\ 1 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 +(-1) \\ 2+1+1 \\ 3+4+1 \\ 4+(-2)+3 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 8 \\ 5 \end{pmatrix} $$

The possibilities continue from here.

The Midpoint Method in Vector Addition

When tasked with calculating the sum of two vectors aligned in the same direction, I employ the midpoint method. This involves identifying the midpoint, M, between the two vector endpoints and then doubling the segment OM.

This method is particularly useful for geometrically summing two vectors that are aligned, even if they possess the same direction but opposite magnitudes.

It's important to note that if vectors are aligned with opposing magnitudes, the traditional parallelogram method falls short. This is because the vectors would form a degenerate parallelogram. In such scenarios, the midpoint method proves invaluable. Conversely, when vectors are aligned and share the same magnitude, the process is straightforward: one can either add the two magnitudes directly or geometrically extend one vector over the other.

Proof of Concept

Within any parallelogram, the diagonals intersect at the midpoint of two opposing vertices.

Given that the segment OC represents the magnitude of the vector sum v+w, I introduce a secondary diagonal (AB) to pinpoint the midpoint, M.

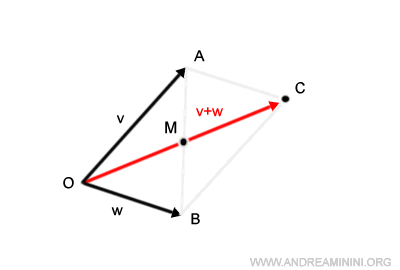
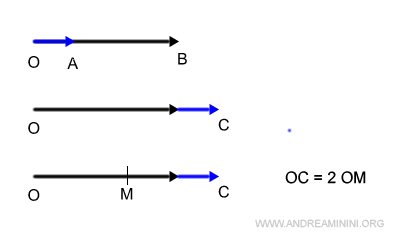
The midpoint, M, boasts two pivotal geometric properties:

1. It maintains an equal distance from points O and C, denoted as $$ OM=MC $$
2. The segment OM is precisely half the magnitude of the sum vector (OC), expressed as $$ OC = 2 \cdot OM $$

Armed with these insights, I can adeptly calculate the sum of two vectors sharing the same direction.

To illustrate, I determine the midpoint between the opposing vertices A and B, resulting in the segment OM.

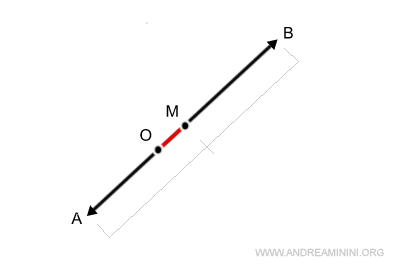
Recognizing that OM represents half the length of the sum vector, I simply double this segment to obtain 2 OM, thereby revealing the magnitude of the sum vector.

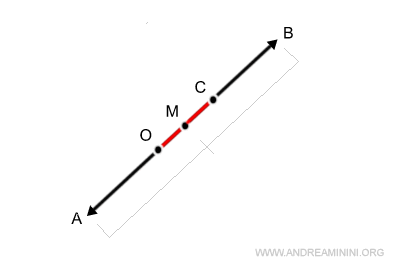
This is the the sum vector:

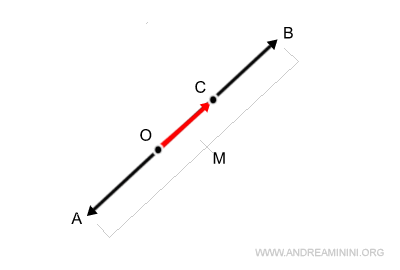
A Brief Note on the Sum Vector. While the midpoint method is applicable to vectors that are aligned with the same magnitude, this scenario is rather elementary. To find the midpoint, M, one would sum the lengths of the two vectors, halve this sum to identify M, and then double M to derive the sum vector. However, this sequence is somewhat redundant. When vectors share the same magnitude, it's more efficient to directly sum the vector lengths without the intermediary step of midpoint calculation.

The Essence of the Triangle Inequality

When I delve into the world of vectors, one principle that consistently stands out is the triangle inequality. Simply put, if you take the magnitude (or norm) of the sum of two vectors, it's always going to be less than or equal to the combined magnitudes of those individual vectors. Mathematically, this relationship is expressed as: $$ | \vec{v} + \vec{w} | \le |\vec{v}|+|\vec{w}| $$

Now, you might wonder why it's termed the "triangle inequality."

Well, the name draws inspiration from a fundamental property of triangles. In any given triangle, if you sum up the lengths of any two sides, that total will always surpass the length of the third side.

Interestingly, there's a unique scenario where the magnitude of the sum matches the sum of the magnitudes. This occurs when the vectors are either parallel or perfectly overlapping, moving in the same direction. In mathematical terms:

$$ | \vec{v} + \vec{w} | = |\vec{v}|+|\vec{w}| $$

In such instances, the resulting vector from the sum retains the same direction and orientation as its constituents.

And so on.