Distance Between Vectors
Vector distance is a way of quantifying how far apart two vectors are in space. It's typically computed using the norm of their difference: \[ d(\vec{v}, \vec{w}) = |\vec{v} - \vec{w}| \]
Imagine two points in three-dimensional space - though the same reasoning applies in any number of dimensions.
Suppose one point is located at \(\vec{v} = (x_1, y_1, z_1)\), and the other at \(\vec{w} = (x_2, y_2, z_2)\).
The distance between them is simply the magnitude (or norm) of the difference vector \(\vec{v} - \vec{w}\):
\[ |\vec{v} - \vec{w}| = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2} \]
This formula is a direct generalization of the Pythagorean theorem to three-dimensional space.
Note. When referring to the distance between vectors, we usually mean the Euclidean norm - the square root of the sum of the squared differences. However, other norms are also used in certain contexts. For example, the Manhattan distance (also known as taxicab or L1 distance) is given by \(|x_1 - x_2| + |y_1 - y_2| \), while the Chebyshev distance (or L∞ norm) is \(\max(|x_1 - x_2|, |y_1 - y_2|)\).
Worked Example
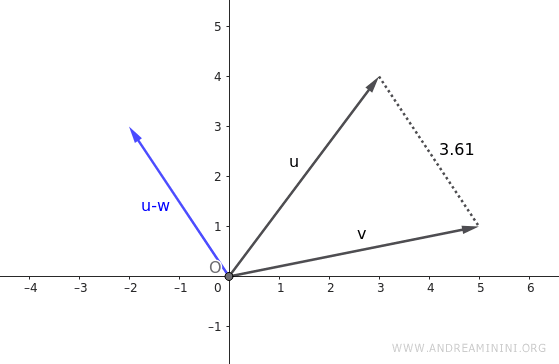
Let’s consider two vectors in \(\mathbb{R}^2\):
\[ \vec{v} = \begin{pmatrix} 3 \\ 4 \end{pmatrix} \]
\[ \vec{w} = \begin{pmatrix} 5 \\ 1 \end{pmatrix} \]
We begin by calculating their difference:
\[ \vec{v} - \vec{w} = \begin{pmatrix} 3 - 5 \\ 4 - 1 \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} \]
The magnitude of the resulting difference vector is:
\[ |\vec{v} - \vec{w}| = \sqrt{(-2)^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \]
So the distance between the two vectors is \(\sqrt{13}\), which is approximately 3.6 units.
Distance in Higher-Dimensional Spaces
The same formula applies in spaces of any dimension.
For instance, take two vectors in four-dimensional space \(\mathbb{R}^4\):
\[ \vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} \]
\[ \vec{b} = \begin{pmatrix} 3 \\ 0 \\ -1 \\ 2 \end{pmatrix} \]
Their difference is:
\[ \vec{a} - \vec{b} = \begin{pmatrix} -2 \\ 2 \\ 4 \\ 2 \end{pmatrix} \]
And the Euclidean distance is:
\[ |\vec{a} - \vec{b}| = \sqrt{(-2)^2 + 2^2 + 4^2 + 2^2} = \sqrt{4 + 4 + 16 + 4} = \sqrt{28} \approx 5.29 \]
Note. In high-dimensional spaces, vector distance is a core concept in computer science. It's widely used to measure similarity between data points - such as images, text documents, or user profiles - and plays a key role in 3D graphics, pattern recognition, and machine learning algorithms like k-nearest neighbors (k-NN) and clustering.
And so on.
