Moment of a Vector

What is the moment of a vector?

The moment of a vector v, applied at a point P with respect to a point O (called the pole), is defined as the cross product of the position vector OP and the vector v itself. $$ \vec{M} = \vec{OP} × \vec{v} $$ The magnitude of the moment is given by: $$ | \vec{M} | = | \vec{OP} | \cdot | \vec{v} | \cdot \sin θ $$

Here, θ is the angle between vectors v and OP.

The moment of a vector is itself a vector quantity.

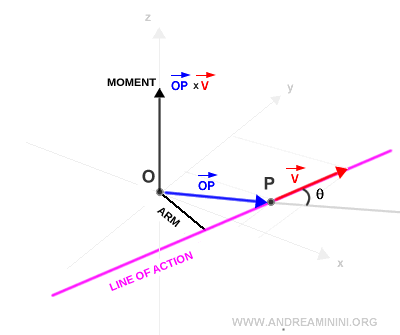
It is a vector perpendicular to the plane containing both v and the position vector OP, since it results from a vector cross product.

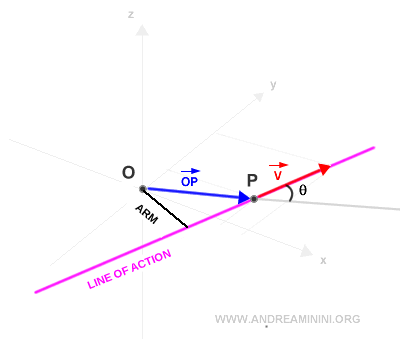
Note. The direction of vector v is referred to as its line of action. The shortest distance between this line of action and the pole O is called the moment arm of vector v relative to pole O.

Properties of the moment of a vector

Here are the key properties of the moment of a vector:

• The magnitude of the moment is zero when vectors v and OP share the same direction. In other words, the moment vanishes if the vectors are parallel or coincide. It is non-zero if they point in different directions.
  

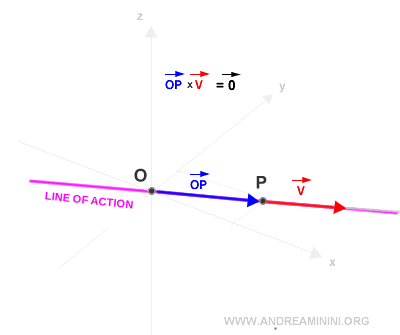
  Note. In this case, the moment arm is zero because the line of action passes through the pole O. The moment vector is thus zero.

• Translating vector v along its line of action does not affect the magnitude of its moment. This highlights an important conservation property of the moment.
  

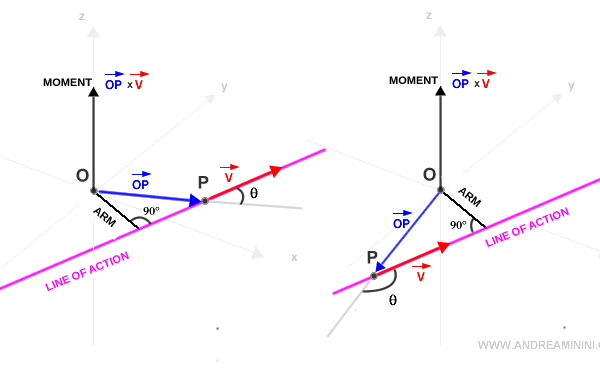
Step-by-step explanation

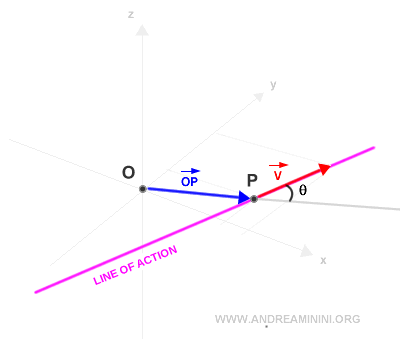
Let’s consider a vector applied at point P and a reference point O, which serves as the pole.

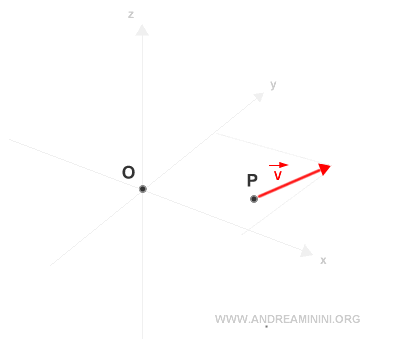
First, we calculate the position vector of v with respect to O.

Next, we draw the lines representing the directions of both vectors.

The direction of vector v defines its line of action.

We then measure the angle θ between the two vectors.

The perpendicular distance from the line of action to the pole is called the moment arm.

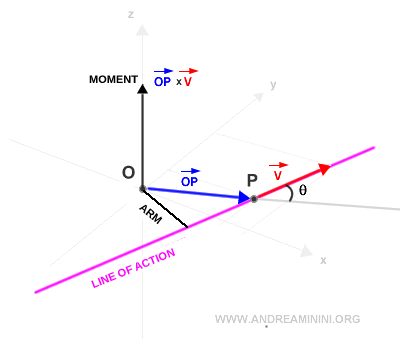
Now, we compute the cross product of the position vector OP and the vector v.

The result is a vector perpendicular to the plane - this is the moment of vector v with respect to pole O.

Effect of changing the pole

The pole serves as the reference point (or frame of reference).

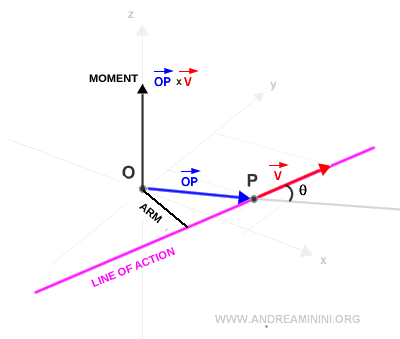
Changing the pole from O to a new point O' in the Cartesian plane alters the moment of the vector.

The new moment vector M_O' retains the same direction as the original moment, but its magnitude will generally change.

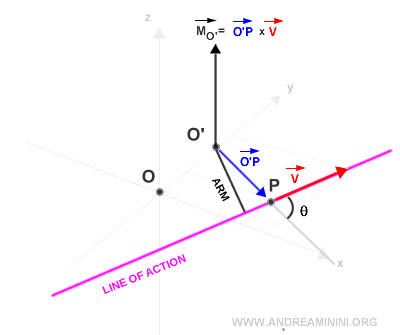
Changing the pole affects the angle θ, the moment arm, and the magnitude of the moment.

The two moments M_O and M_O' of vector v are related by the following algebraic expression:

$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$

Proof

The moment of vector v with respect to pole O is given by:

$$ \vec{M_O} = \vec{OP} × \vec{v} $$

The moment of vector v with respect to pole O' is given by:

$$ \vec{M_{O'}} = \vec{O'P} × \vec{v} $$

The position vector O'P is equivalent to the sum of vectors O'O and OP.

Therefore:

$$ \vec{M_{O'}} = ( \vec{O'O} + \vec{OP} ) × \vec{v} $$

Applying the distributive property of the cross product:

$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{OP} × \vec{v} $$

Since M_O = OP × v, it follows that:

$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$

This completes the proof of the relationship between the two moments of the vector with respect to poles O and O'.

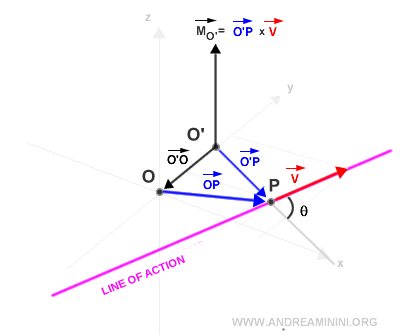
Thus, the magnitude of the new moment |M_O'| after changing the reference frame is:

$$ | \vec{M_{O'}} | = | \vec{O'O} × \vec{v} | + | \vec{M_O} | $$

 

Note. If, after changing the pole, vector O'O is parallel to vector v, the moment remains unchanged because the moment arm is unaffected. $$ \vec{O'O} \ || \ \vec{v} \ \ \Rightarrow \ \ M_{O'}=M_O $$ The following diagram illustrates this special case:

And so on.