Parallel Vectors

Two vectors in a plane are said to be parallel if they are linearly dependent.

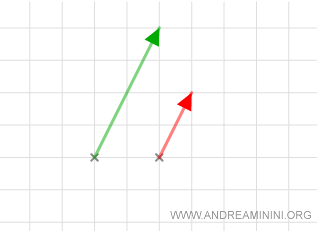
A Practical Example

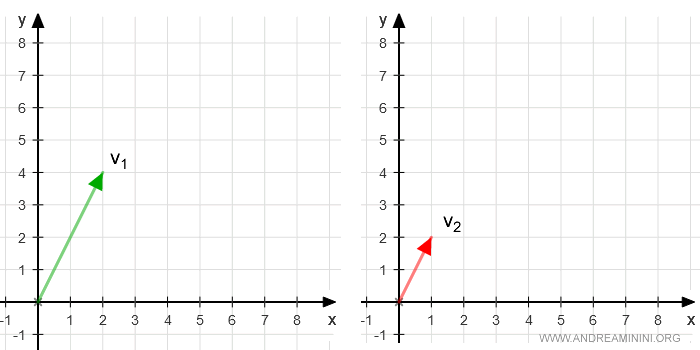
Consider two vectors v₁ and v₂ in the vector space V=R² over the field K=R

$$ v_1 = \overrightarrow{AB} = ( 2,4 ) \\ v_2 = \overrightarrow{CD} = ( 1,2 ) $$

These two vectors are linearly dependent if the determinant of the matrix formed by the two column vectors is zero.

$$ det \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} = 0 $$

This means that the two vectors are proportional to each other.

Note: In this case, vector AB is twice vector CD. $$ \overrightarrow{CD} = 2 \cdot \overrightarrow{AB} = 2 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$

The rank of the matrix of the column vectors is one or less.

$$ rg \begin{pmatrix} 2 & 1 \\ 4 & 2 \end{pmatrix} \le 1 $$

Demonstration

Graphically representing both vectors from the origin O(0,0)

It's immediately clear that the two vectors are proportional, as they lie on the same line passing through the origin.

One vector is a multiple of the other. There exists a scalar k such that v₁=k·v₂.

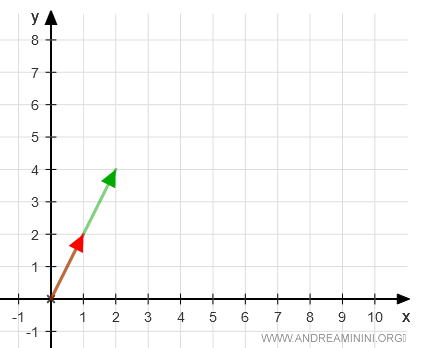
This demonstrates the linear dependence of the two vectors.

And so on.

Corollaries

• Vector Parallel to a Line

  A vector is parallel to a line r in the plane if it lies on a line parallel to line r or on line r itself.

• Vector Applied to a Point

  Any point P in the plane generates an applied vector PP parallel to every line in the plane.

Parallel Vectors in Space

In a three-dimensional space R³

A vector is parallel to a line if it has the same direction vector or the same normal vector.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \\ n \end{pmatrix} $$

Where (l,m,n) is the direction vector of the vector equation while (x₀,y₀,z₀) is any point on the line.

A direction vector determines the direction of all lines parallel to the vector itself.

A vector is parallel to a plane if it lies on a parallel plane.