Vector, Parametric, and Cartesian Equations of a Plane

A plane is defined by two linearly independent geometric vectors in distinct directions and a point lying on the plane.

$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

$$ P_0 = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Without specifying the point P₀, the two geometric vectors v₁ and v₂ would represent all planes parallel to these vectors, rather than a specific plane.

Therefore, every point on a plane can be described by the following vector equation of the plane.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

From the vector equation, it's straightforward to derive the parametric equations of the plane.

$$ \begin{cases} x = x_0 + t_1 \cdot l_1 + t_2 \cdot l_2 \\ y = y_0 + t_1 \cdot m_1 + t_2 \cdot m_2 \\ z = z_0 + t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$

The parametric equations can be rewritten in this form:

$$ \begin{cases} x - x_0 = t_1 \cdot l_1 + t_2 \cdot l_2 \\ y - y_0 = t_1 \cdot m_1 + t_2 \cdot m_2 \\ z - z_0 = t_1 \cdot n_1 + t_2 \cdot n_2 \end{cases} $$

This results in three vectors P₀P, v₁, and v₂, which can be arranged in a square matrix.

$$ \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} $$

Calculating the determinant of this matrix gives us the Cartesian equation of the plane.

$$ det \begin{pmatrix} x - x_0 & l_1 & l_2 \\ y - y_0 & m_1 & m_2 \\ z - z_0 & n_1 & n_2 \end{pmatrix} = $$

$$ (x-x_0) \cdot det \begin{pmatrix} m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} + (y-y_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ n_1 & n_2 \end{pmatrix} + (z-z_0) \cdot det \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \end{pmatrix} $$

A Practical Example

I have two directional vectors

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} \:\:\: v_2 = \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

and a point

$$ P = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$

I'm going to check if these two vectors are linearly independent.

The rank of the vectors equals two. Therefore, they are linearly independent.

$$ r_k = \begin{pmatrix} 3 & 4 \\ 1 & 3 \\ 2 & 1 \end{pmatrix} = 2 $$

Note. If the rank matches the number of vectors, they are linearly independent.

Next, I'll verify if the point P is on the plane.

How to Determine if a Point is on a Plane

If point P lies on the plane, there exist two parameters t₁ and t₂ that solve the following linear combination and its corresponding linear system.

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 v_1 + t_2 v_2 $$

I'll substitute the directional vectors.

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Then, I take the endpoint of one of the vectors as reference point P₀ on the plane.

For instance (3,1,2).

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1\cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Finally, I replace the coordinates (x,y,z) with those of the point (10,5,5) and check if the system has a solution.

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1\cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

The system has a solution.

To obtain the point (10,5,5), I can set the parameters t₁=1 and t₂=1.

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + 1 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 + 3 + 4 \\ 1 + 1 + 3 \\ 2 + 2 + 1 \end{pmatrix} $$

$$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} $$

Therefore, the vector equation of the plane is as follows:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

An Alternative Check. To verify the solution's existence, I could have transformed the vector equation into three vectors $$ \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 10-3 \\ 5-1 \\ 5-2 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ $$ \begin{pmatrix} 7 \\ 4 \\ 3 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$ Then arrange the vectors of coefficients in a matrix column. $$ \begin{pmatrix} 7 & 3 & 4 \\ 4 & 1 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ If the rank of the matrix is less than the number of vectors, meaning less than three, then the vectors are linearly dependent, and the system has a solution. In this case, the rank of the matrix is two (r_k=2). Therefore, the system has a solution. $$ r_k = 2 < 3 $$ The explanation is straightforward. The vectors v₁(3,1,2) and v₂(4,3,1) are linearly independent. For the first vector (7,1,3) to be part of the plane, it must be linearly dependent on v1 and v2.

Once I have the vector equation, I can easily calculate the parametric equation of the plane.

I just need to transform it into a system of equations.

$$ \begin{cases} x = 10 + t_1 \cdot 3 + t_2 \cdot 4 \\ y = 5 + t_1 \cdot 1 + t_2 \cdot 3 \\ z = 5 + t_1 \cdot 2 + t_2 \cdot 1 \end{cases} $$

$$ \begin{cases} x = 10 + 3t_1 + 4t_2 \\ y = 5 + t_1 + 3t_2 \\ z = 5 + 2t_1 + t_2 \end{cases} $$

Finally, to obtain the Cartesian equation of the plane, I transform the vector equation into three segments.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 10 \\ 5 \\ 5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

$$ \begin{pmatrix} x - 10 \\ y - 5 \\ z-5 \end{pmatrix} = t_1 \cdot \begin{pmatrix} 3 \\ 1 \\ 2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 4 \\ 3 \\ 1 \end{pmatrix} $$

Then I arrange the three vectors in a column within a matrix.

$$ \begin{pmatrix} x - 10 & 3 & 1 \\ y - 5 & 1 & 3 \\ z-5 & 2 & 1 \end{pmatrix} $$

The determinant of the matrix is the Cartesian equation of the plane.

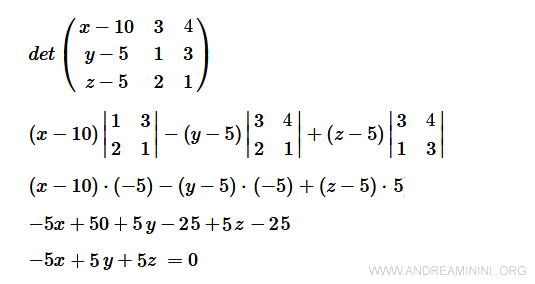
This way, I have also found the Cartesian equation of the plane.

The graphical representation of the plane in a three-dimensional diagram is as follows:

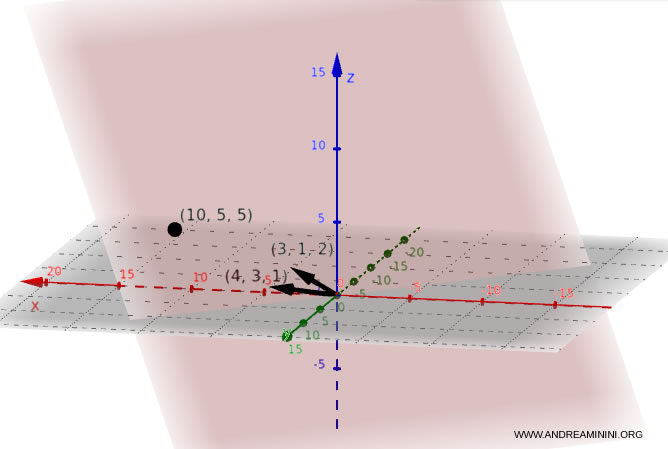
Converting from Cartesian to Parametric Equations of a Plane

Let's explore the reverse process. I know the Cartesian equation of a plane and want to derive its parametric equation.

The Cartesian equation of the plane is:

$$ ax + by + cz + d = 0 $$

The corresponding vector-parametric equation of the plane is:

$$ P = P_0 + t_1 v_1 + t_2 v_2 $$

The coefficients a, b, c in the Cartesian equation define the normal vector of the equation, that is, a vector perpendicular to the plane.

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} $$

If the normal vector is perpendicular to the plane, it's also perpendicular to any vector in the plane.

Thus, the normal vector is orthogonal to the direction vectors of the plane's parametric equation.

Therefore, the dot product between the normal vector and the direction vectors is zero.

$$ \langle n , v_2 \rangle = 0 $$

$$ \langle n , v_1 \rangle = 0 $$

This relationship allows me to find two linearly independent vectors orthogonal to the normal vector and construct the plane's vector/parametric equation.

Example

Consider the following Cartesian equation:

$$ -5x -y +8z + 15 = 0 $$

The normal vector to this equation is:

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$

This normal vector is orthogonal to the Cartesian plane.

It is therefore orthogonal to all non-zero vectors in the plane.

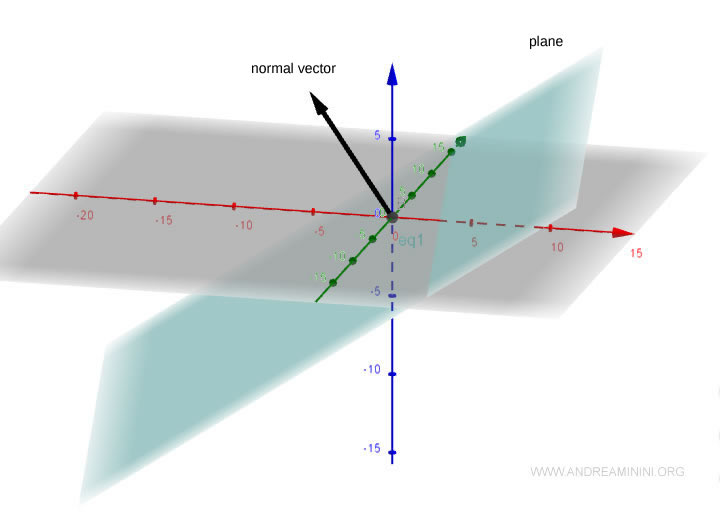
Next, I need to find two linearly independent vectors orthogonal to the normal vector.

To do this, I nullify one coordinate of the normal vector, reverse the other two, and change the sign of one of these last two.

For instance, let's nullify the x component of the normal vector.

$$ \begin{pmatrix} 0 \\ -1 \\ 8 \end{pmatrix} $$

Then reverse the other two:

$$ \begin{pmatrix} 0 \\ 8 \\ -1 \end{pmatrix} $$

Next, change the sign of one of these last two coordinates.

Now, I've found the first direction vector of the plane's equation.

$$ v_1 = \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} $$

Using the same method, I also find the second direction vector.

For example, let's nullify the y component.

$$ \begin{pmatrix} -5 \\ 0 \\ 8 \end{pmatrix} $$

Reverse the remaining coordinates:

$$ \begin{pmatrix} 8 \\ 0 \\ -5 \end{pmatrix} $$

Then change the sign of one of these last two coordinates.

$$ v_2 = \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

I have found two vectors orthogonal to the normal vector.

I verify that they are linearly independent vectors.

$$ r_k \begin{pmatrix} 0 & 8 \\ 8 & 0 \\ 1 & 5 \end{pmatrix} = 2 $$

The rank of the matrix with the vectors in columns is equal to 2, which is the number of vectors.

Therefore, the two vectors are linearly independent.

Now, I confirm that they are also orthogonal to the normal vector.

$$ \langle n , v_1 \rangle = \langle \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} \rangle = 0 $$

$$ \langle n , v_2 \rangle = \langle \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} , \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} \rangle = 0 $$

The dot product is zero.

Therefore, the vectors v₁ and v₂ are orthogonal vectors to the normal vector.

I can use them as direction vectors of the plane.

Once their linear independence and orthogonality are confirmed, I can replace direction vectors v₁ and v₂ in the plane's vector equation.

$$ P = P_0 + t_1 v_1 + t_2 v_2 $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

This is the parametric equation of the plane and all parallel planes.

To restrict the equation to the specific plane of interest, I just need to add any point P₀ on the plane.

For example, I assign x=0 and z=0 in the Cartesian equation to determine the y-coordinate.

$$ -5x -y +8z + 15 = 0 \\ -5(0) -y +8(0) + 15 = 0 \\ y =15$$

Thus, I've obtained an arbitrary point on the plane P(x,y,z)=(0,15,0).

Substituting this into the vector equation in place of P₀, I've found the vector equation of the plane.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 15 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ 8 \\ 1 \end{pmatrix} + t_2 \begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} $$

Having found the vector equation, it's easy to convert to the parametric equation of the plane.

I simply transform the vectors into a system of equations.

$$ \begin{cases} x = 8t_2 \\ y = 15 +8 t_1 \\ z = t_1 + 5t_2 \end{cases} $$

Finding the Cartesian Equation from the Normal Vector

Consider the following Cartesian equation:

$$ -5x -y +8z + 15 = 0 $$

The normal vector of this equation is:

$$ n = \begin{pmatrix} a \\ b \\ c \end{pmatrix} = \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} $$

The normal vector is orthogonal to the Cartesian plane.

Let's select an arbitrary point on the plane.

To find the x-coordinate, set y and z to zero.

$$ -5x -y +8z + 15 = 0 $$

$$ -5x -(0) +8(0) + 15 = 0 $$

$$ x = 15 $$

This gives us a point P₁ on the plane.

$$ P_1 = \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} $$

Now, consider a generic point on the plane:

$$ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

Calculate the segment between the two points.

$$ P_1P= \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 15 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} x -15\\ y \\ z \end{pmatrix} $$

This gives us a generic vector v in the plane.

We know that any vector in the plane must be orthogonal to the normal vector.

Therefore, the dot product <v,n> is zero.

$$ < P_1P , n > = 0 $$

Perform the calculations for the dot product:

$$ < \begin{pmatrix} x -15\\ y \\ z \end{pmatrix} , \begin{pmatrix} -5 \\ -1 \\ 8 \end{pmatrix} > = -5(x-15)-y+8z = 0 $$

$$ -5x+75-y+8z = 0 $$

This leads us to the Cartesian equation of the plane:

And so on