Decomposing a Vector

When we talk about decomposing a vector, we're essentially breaking it down into its individual components along the Cartesian axes. In other words, a vector \( \vec{v} \) can be expressed as the sum of its components \( \vec{v_x} \), \( \vec{v_y} \), and \( \vec{v_z} \): $$ \vec{v} = \vec{v_x} + \vec{v_y} + \vec{v_z} $$ This can also be rewritten as a linear combination of the unit vectors $$ \vec{v} = \alpha_1 \vec{u_x} + \alpha_2 \vec{u_y} + \alpha_3 \vec{u_z} $$

Here, the unit vectors u_x, u_y, u_z represent the standard directions in a 3D Cartesian coordinate system (x, y, z).

The scalars α₁, α₂, α₃ are specific values chosen for the decomposition.

So, what exactly are these vector components? They're the projections of the vector onto the Cartesian axes. For instance, consider the components \( \vec{v_x} \) and \( \vec{v_y} \) of a vector \( \vec{v} \) in a 2D Cartesian plane (x,y).

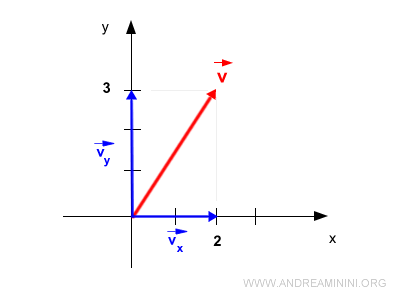
These components themselves are vector quantities, not scalars.

A Practical Example

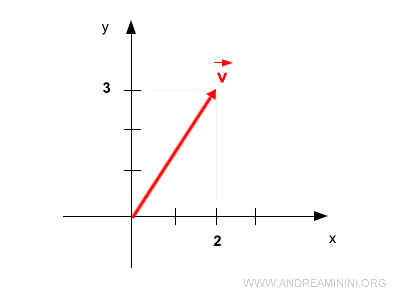
Let's take a 2D vector v=(2,3)^T represented as:

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Here's its graphical representation.

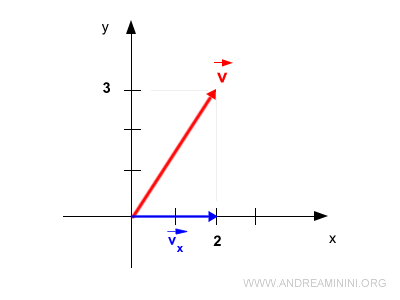
When we project \( \vec{v} \) onto the x-axis, we get its x-component.

 

Similarly, projecting onto the y-axis gives the y-component.

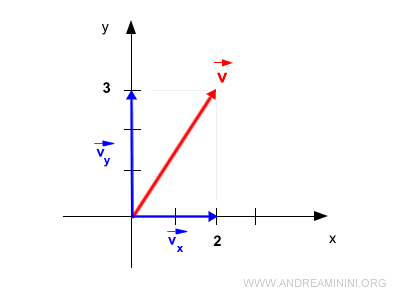
Both \( \vec{v_x} \) and \( \vec{v_y} \) are vector quantities.

Thus, the components in both directions are:

 

$$ \vec{v_x} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} $$

$$ \vec{v_y} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

The vector sum of \( \vec{v_x} \) and \( \vec{v_y} \) gives back our original vector \( \vec{v} \).

$$ \vec{v_x} + \vec{v_y} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \vec{v} $$

We can express the components \( \vec{v_x} \) and \( \vec{v_y} \) as the product of the corresponding unit vector and a scalar.

$$ \vec{v_x} = x \cdot \vec{u_x} $$

$$ \vec{v_y} = y \cdot \vec{u_y} $$

For instance, with coordinates x=2 and y=3:

$$ \vec{v_x} = 2 \cdot \vec{u_x} $$

$$ \vec{v_y} = 3 \cdot \vec{u_y} $$

Given that the unit vectors in Cartesian coordinates are \( \vec{u_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \) and \( \vec{u_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \), we can express the sum of the components as:

$$ \vec{v_x} + \vec{v_y} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

The sum of the components equals the vector \( \vec{v} \).

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

This linear combination of unit vectors with scalars allows us to retrieve our initial vector \( \vec{v} \).

$$ \vec{v} = \vec{v_x} + \vec{v_y} $$

$$ \vec{v} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 3 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

$$ \vec{v} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 3 \end{pmatrix} $$

$$ \vec{v} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Note. The magnitudes of the components \( \vec{v_x} \) and \( \vec{v_y} \) can also be expressed using trigonometric functions: $$ | \vec{v_x} | = r \cdot \sin \Phi $$ $$ | \vec{v_y} | = r \cdot \cos \Phi $$ Where \( \Phi \) is the angle the vector makes with the x-axis and r is the vector's magnitude.

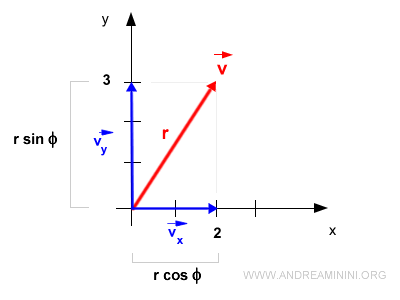
The magnitude can be found using the Pythagorean theorem: $$ r = \sqrt{ |\vec{x}|^2 + |\vec{y}|^2 } $$ $$ r = \sqrt{ 2^2 + 3^2 } $$ $$ r = \sqrt{ 4 + 9 } $$ $$ r = \sqrt{ 13 } $$

Example 2

If the vector is positioned at a point other than the origin, its projection needs to be calculated both at the vector's endpoint and its origin.

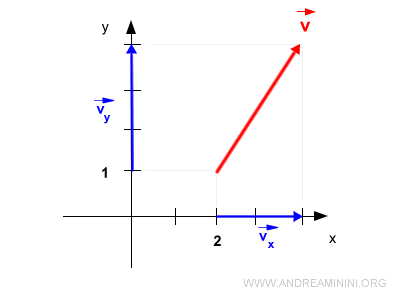
And so on.