One-to-One Mapping Between Vectors and Points in the Plane

Every point $ P $ in the plane, defined by its coordinates $ (x, y) $, can be uniquely associated with a vector $ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $. This vector, known as the position vector, originates from the origin $ O $ and terminates at $ P $. The reverse association also holds true.
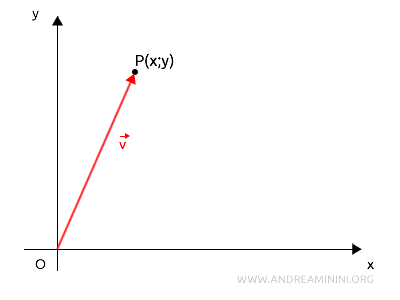
example

In other words, there is a perfect one-to-one relationship between points in the plane $ P $ and vectors in the vector space $ \mathbb{R}^2 $.

This means that points in the plane and vectors in $ \mathbb{R}^2 $ can be seen as "two perspectives on the same concept": a point can be represented by a vector, and a vector specifies a unique point.

This correspondence depends on choosing an origin $ O $, which serves as the reference point for defining position vectors.

The mapping between points in the plane and vectors in $ \mathbb{R}^2 $ is one-to-one because:

Each point in the plane corresponds to a unique position vector
Every point $ P(x, y) $ is represented by exactly one vector $ \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix} $.
Each vector corresponds to a unique point
Any vector $ \begin{pmatrix} x \\ y \end{pmatrix} $ corresponds to a single point $ P(x, y) $ in the plane.

Example

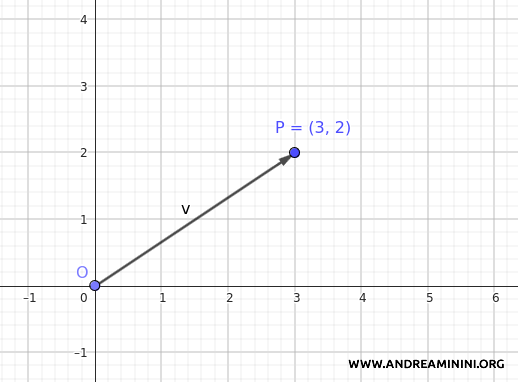
For example, if a point in the plane has coordinates $ P(3, 2) $, its corresponding vector is:

$$ \vec{OP} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

Conversely, given a vector $ \vec{v} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $, it can be associated with the point $ P(3, 2) $ in the plane.

a practical example

And so on.