Vector Subtraction
When working with vectors, it's essential to understand the concept of subtraction. Let's dive into it.
Given two vectors, v and w, with an identical number of components, the subtraction v-w is achieved by subtracting the coordinates of v from those of w. Mathematically, this is represented as: $$ \vec{v} - \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} - \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 - w_1 \\ v_2 - w_2 \\ \vdots \\ v_n - w_n \end{pmatrix} $$ The result? The difference vector.
It's crucial to note that vector subtraction is only feasible when both vectors have the same number of components. If they don't, the operation isn't valid.
Example
Let's illustrate this with an example.
Consider the vectors:
$$ \vec{v} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
Here, v is our minuend and w is the subtrahend.
$$ \vec{v} - \vec{w} $$
Subtracting the coordinates of v from w gives:
$$ \vec{v} - \vec{w} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} - \begin{pmatrix} 4 \\ 3 \end{pmatrix} = \begin{pmatrix} 2-4 \\ 5-3 \end{pmatrix} = \begin{pmatrix} -2 \\ 2 \end{pmatrix} $$
This result is our difference vector.
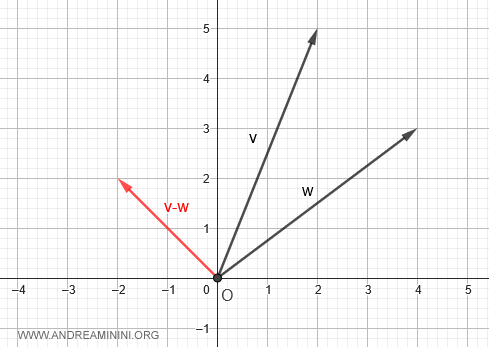
The graphical method
For those who prefer a visual approach, let's explore the graphical method:
For instance, with the vectors:
$$ \vec{v} = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$
Plot these vectors on a Cartesian plane.
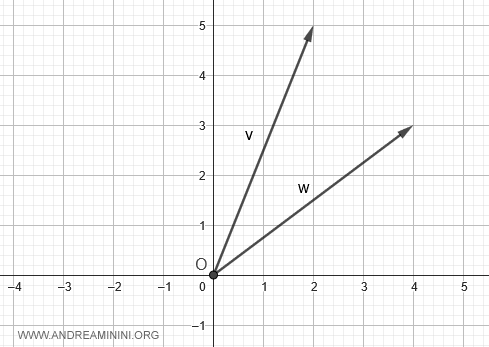
To subtract the two vectors:
$$ \vec{v} - \vec{w} $$
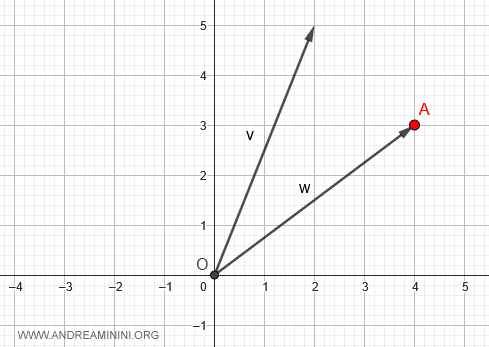
When plotting vectors on a plane, start at the point where the subtrahend vector, w, is applied, say point A with coordinates (4,3).
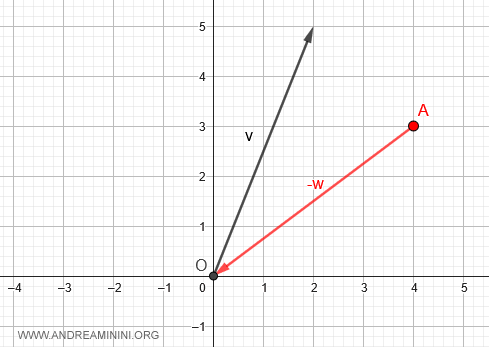
From there, apply the opposite vector, -w, moving towards the origin (O).
Next, apply the minuend vector, v, leading you to point B with coordinates (2,5).
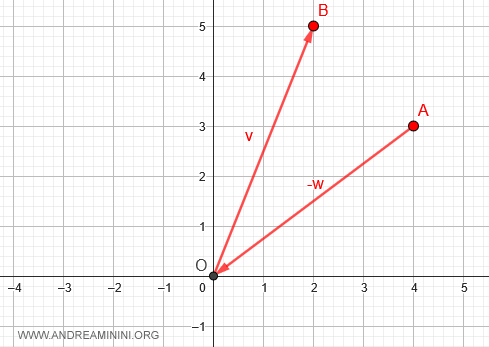
Connecting points A and B gives you a directed segment.
In physics, this is often referred to as the displacement vector, showcasing the movement from one point to another.
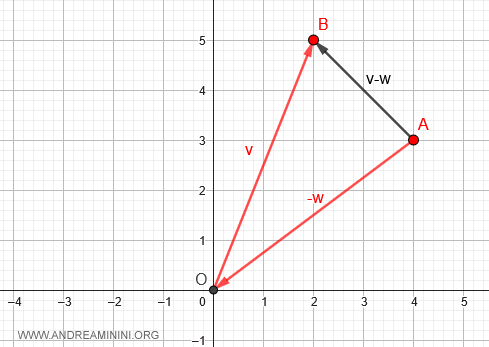
To finalize, simply shift the base of the displacement vector to the origin (O).
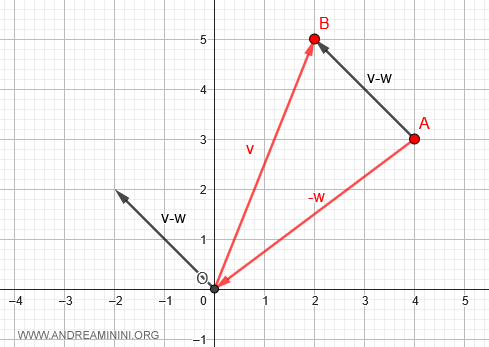
The resulting vector represents the difference between v and w.
I hope this provides a clear understanding of vector subtraction.
