Unit Vectors

What is a unit vector?

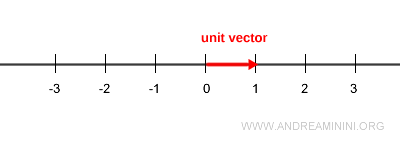
A unit vector is a vector with a magnitude (length) of exactly 1, pointing in a specific direction.

Any given direction (a line) contains infinitely many vectors of varying lengths, pointing either way along that line.

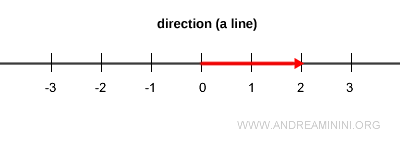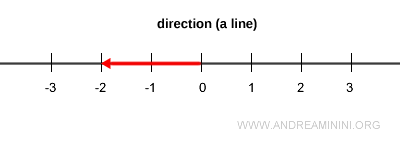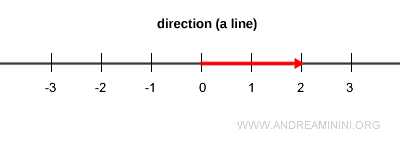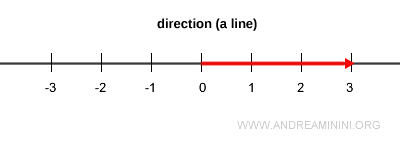
infinite-length vectors along a given direction

However, there is only one vector in that direction whose length is exactly one - the unit vector.

visual explanation of a unit vector

Why is it called a unit vector?

The term “unit” refers to its length - precisely one. It defines direction and orientation (sense) along a line.

What is a unit vector used for?

Any other vector in the same direction can be obtained by scaling the unit vector by a real number $ k $.

Example
Unit Vectors Along the Coordinate Axes

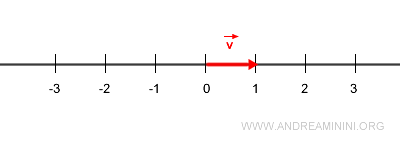
Example

Let $ \vec{v} $ be a unit vector.

unit vector v

Suppose $ \vec{w} $ is a vector with magnitude 3.

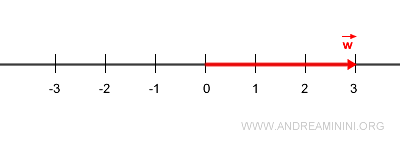
vector w with magnitude 3

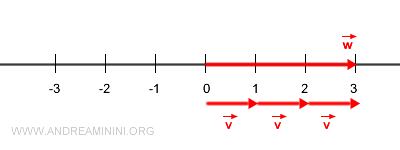
Then $ \vec{w} $ can be written as the product of $ \vec{v} $ and the scalar 3:

$$ \vec{w} = 3 \cdot \vec{v} $$

This yields a vector in the same direction as $ \vec{v} $, but three times as long.

scalar multiplication to produce vector w

Example 2

Again, let $ \vec{v} $ be a unit vector.

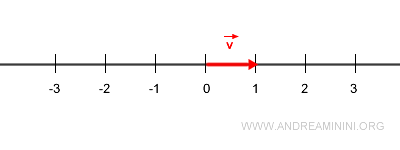
unit vector v

Now, consider a vector $ \vec{u} $ of magnitude 2, pointing in the opposite direction.

vector u in the opposite direction

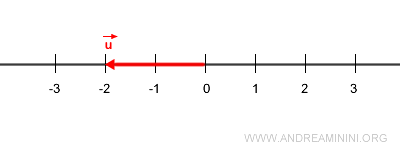
Note. The magnitude of $ \vec{u} $ is 2. It would be incorrect to say its magnitude is - 2: magnitudes are always positive. The sign indicates the direction relative to the unit vector.

We obtain $ \vec{u} $ by multiplying $ \vec{v} $ by - 2:

$$ \vec{w} = -2 \cdot \vec{v} $$

The negative scalar reverses the direction of the vector:

$$ \vec{w} = 2 \cdot (-\vec{v}) $$

Here, $ -\vec{v} $ is the opposite vector of $ \vec{v} $.

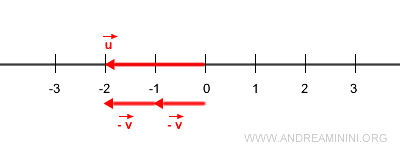
multiplying by a negative scalar flips the direction

In short, once you have the unit vector, you can generate any vector along that line through scalar multiplication.

Unit Vectors Along the Coordinate Axes

Any vector in three-dimensional Cartesian space can be expressed as a linear combination of the unit vectors along the x-, y-, and z-axes: $$ \vec{w} = \alpha_1 \cdot \vec{u_x} + \alpha_2 \cdot \vec{u_y} + \alpha_3 \cdot \vec{u_z} $$

These unit vectors are commonly denoted $ \vec{u_x} $, $ \vec{u_y} $, and $ \vec{u_z} $, or simply $ \hat{i} $, $ \hat{j} $, and $ \hat{k} $.

The coefficients $ \alpha_1 $, $ \alpha_2 $, and $ \alpha_3 $ are scalars - real numbers.

Example

In two-dimensional space, we only need two unit vectors: $ \vec{u_x} $ and $ \vec{u_y} $.

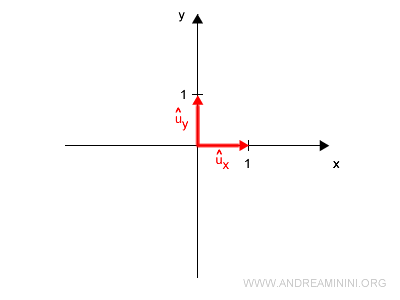
unit vectors in 2D Cartesian space

Note. For simplicity, we use the unit vectors of the canonical basis: $$ \vec{u_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \vec{u_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Of course, any pair of linearly independent vectors in the space could serve as a basis.

The linear combination of these unit vectors can represent any vector in the space.

For example, to construct $ \vec{w} = (2,1)^T $:

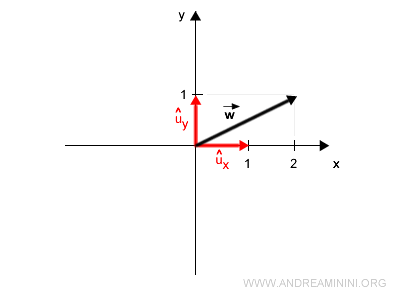
constructing w using a linear combination of unit vectors

Note. The superscript $ T $ indicates the transpose - converting a row vector into a column vector: $$ \vec{w} = \begin{pmatrix} 2 , 1 \end{pmatrix}^T = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$

We express $ \vec{w} $ as:

$$ \vec{w} = \alpha_1 \cdot \vec{u_x} + \alpha_2 \cdot \vec{u_y} $$

with $ \alpha_1 = 2 $ and $ \alpha_2 = 1 $:

$$ \vec{w} = 2 \cdot \vec{u_x} + 1 \cdot \vec{u_y} $$

Substituting the unit vectors in component form:

$$ \vec{w} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

Performing the scalar multiplications:

$$ \vec{w} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$

And summing the vectors gives:

$$ \vec{w} = \begin{pmatrix} 2+0 \\ 0+1 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$

Using this method, any vector in Cartesian space can be constructed from unit vectors.

And so on.