Opposite Vector

The opposite vector of $ \vec{v} $ is a vector $ -\vec{v} $ characterized by the same direction and magnitude (length) but with the opposite orientation.

To find the opposite vector, simply multiply the vector v by the scalar -1 through the operation of scalar multiplication.

A Practical Example

Consider a vector with a magnitude of 3.

The line on which the vector lies is the direction, while its length (magnitude) is 3.

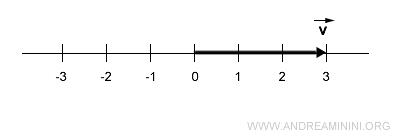
The opposite vector is one along the same line (direction) with the same length (3) but in the opposite direction.

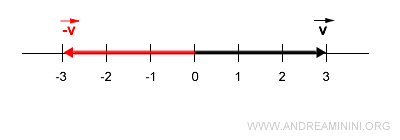
Example 2

Now, consider a vector in a two-dimensional space

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

In a Cartesian diagram, the vector connects the origin O with the point at coordinates (1,2).

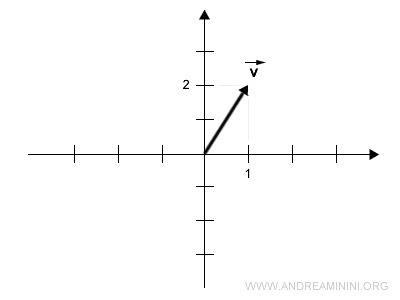
To calculate the opposite vector, compute the product of vector v by the scalar -1.

$$ - \vec{v} = -1 \cdot \vec{v} $$

$$ - \vec{v} = -1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \cdot 1 \\ -1 \cdot 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \\ -2 \end{pmatrix} $$

The opposite vector connects the origin with the point at coordinates (-1,-2).

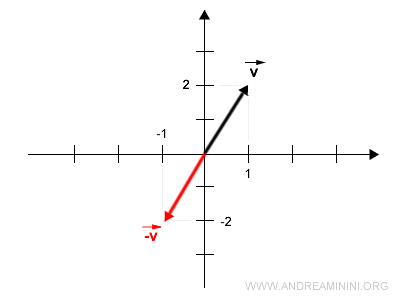
Additional Notes

Some personal reflections and insights on opposite vectors

• The sum of two opposite vectors is always the zero vector
  Let \( \vec{v} \) be a vector in a vector space \( V \). Its opposite, denoted by \( -\vec{v} \), is defined as the vector that, when added to \( \vec{v} \), produces the zero vector. $$ \vec{v} + (-\vec{v}) = \vec{0} $$ This property stems directly from the definition of an opposite vector and the associative and commutative properties of vector addition.

  Example. Consider the vector \( \vec{v} \) in the vector space \( \mathbb{R}^2 \): $$ \vec{v} = \begin{pmatrix} 3 \\ -2 \end{pmatrix} $$ Its opposite, \( -\vec{v} \), is: $$ -\vec{v} = \begin{pmatrix} -3 \\ 2 \end{pmatrix} $$ Now, calculate the sum of \( \vec{v} \) and \( -\vec{v} \): $$ \vec{v} + (-\vec{v}) = \begin{pmatrix} 3 \\ -2 \end{pmatrix} + \begin{pmatrix} -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 - 3 \\ -2 + 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ The result is the zero vector: \( \vec{0} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \).

And so on.