Linear Dependence and Independence of Vectors

Given m vectors v₁, v₂, ..., v_m in a vector space V over a field K, these vectors are linearly independent if the linear combination with m scalar coefficients equal to the zero vector has only the trivial solution. $$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 + \ ... \ + \alpha_m \cdot \vec{v}_m = \vec{0} $$ Conversely, if there are other non-trivial solutions, the vectors are linearly dependent.

A linear combination of vectors equal to the zero vector is called trivial when all the scalar coefficients are zero.

$$ a_1 = a_2 = \ ... = \ a_m = 0 $$

If at least one coefficient is different from zero, the solution of the linear combination is non-trivial.

Linearly Independent Vectors

In a vector space V over a field K, vectors v₁,...,v_m ∈ V are linearly independent if no linear combination equals the zero vector, except for the trivial linear combination. $$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} \ \ \ \ \ \ \alpha \in K $$

What is a trivial linear combination?

It's a linear combination of a vector with a sequence of zeros { a₁=0, ..., a_m=0 }.

Why is the trivial linear combination excluded?

The trivial linear combination is not considered because any linear combination of vectors with zero coefficients equals a zero vector.

$$ 0 \cdot v_1 + ... + 0 \cdot v_m = 0 $$

Thus, the trivial solution always exists and cannot inform us about the linear dependence or independence of vectors.

Linearly Dependent Vectors

In a vector space V over the field K, vectors v₁,...,v_m ∈ V are linearly dependent if there exists one or more linear combinations equal to the zero vector, besides the trivial linear combination. $$ \alpha_1 \cdot \vec{v}_1 + ... + \alpha_m \cdot \vec{v}_m = \vec{0} \ \ \ \ \ \ \alpha \in K $$

The trivial solution is excluded because it does not allow to distinguish between linear dependence and independence of vectors.

In this case, there is at least one non-zero scalar coefficient in the linear combination.

From this follows the theorem:

The vectors v₁,...,v_m are linearly dependent if at least one of them (e.g., v₁) can be written as a linear combination of the remaining vectors.

$$ v_1 = \beta_2 \cdot v_2 + ... + \beta_m \cdot v_m $$ $$ with \: \: \beta_2, ..., \beta_m \in R $$

The theorem does not specify which vector can be written as a combination of the others, it only states that there exists one if the vectors are linearly dependent.

It could be any of the vectors v₁,...,v_m and not necessarily v₁.

Geometric Interpretation

In R² space, two vectors are linearly dependent if they are parallel or coincident, i.e., they lie on the same line and have the same direction.

In R³ space, three vectors are linearly dependent if they belong to the same plane.

Note. These geometric considerations can only be made in the case of R² or R³ vector spaces. They cannot be made for vector spaces of higher dimensions such as R^4, R⁵, etc.

A Practical Example

Example 1

Let's consider two vectors in the vector space V=R² over the field of real numbers K=R:

$$ \vec{v}_1 = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

$$ \vec{v}_2 = \begin{pmatrix} 2 \\ 5 \end{pmatrix} $$

The linear combination is as follows:

$$ a_1 \cdot \vec{v}_1 + a_2 \cdot \vec{v}_2 = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ 5 \end{pmatrix} = \vec{0} $$

The null vector is a vector made up of two zeros:

$$ \begin{pmatrix} 3a_1 \\ a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ 5a_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$

I'll rewrite the vector equation as a system of equations:

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ \\ a_1 + 5a_2 = 0 \end{cases} $$

Then, I'll solve the system using the substitution method, isolating a₁ in the second equation:

$$ \begin{cases} 3a_1 + 2a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

Note. Any other method to solve the system is equally valid. For example, the Cramer's rule.

Next, I substitute a₁ into the first equation and find the value of a₂=0.

$$ \begin{cases} 3(-5a_2) + 2a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

$$ \begin{cases}-15a_2 + 2a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

$$ \begin{cases}-13a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = - 5a_2 \end{cases} $$

Once I know a₂, I substitute it into the second equation and get the value of a₁=0.

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = - 5(0) \end{cases} $$

$$ \begin{cases} a_2 = 0 \\ \\ a_1 = 0 \end{cases} $$

The only solution of the system is the null vector, i.e., a₁=0 and a₂=0.

Therefore, the two vectors are linearly independent.

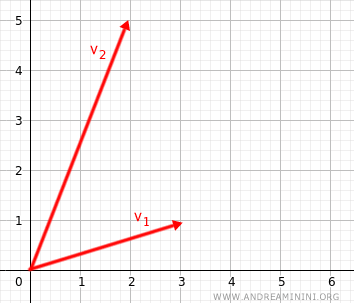
Note. In the case of two vectors in the two-dimensional space R², i.e., on the plane, linear dependence occurs only when the vectors are parallel. Therefore, if the vectors are linearly independent, they are not parallel vectors. However, this characteristic is only valid in the plane and not in higher-dimensional spaces.

Example 2

Consider three vectors in the two-dimensional real vector space V=R²:

$$ \vec{v_1} = \begin{pmatrix} 3 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} $$

$$ \vec{v_3} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$

The three vectors are linearly independent if there isn't a non-trivial linear combination of the three vectors equal to the null vector.

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 1 \\ 4 \end{pmatrix} + a_3 \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \vec{0} $$

$$ \begin{pmatrix} 3a_1 \\ a_1 \end{pmatrix} + \begin{pmatrix} a_2 \\ 4a_2 \end{pmatrix} + \begin{pmatrix} 2a_3 \\ a_3 \end{pmatrix} = \vec{0} $$

To determine if they are linearly independent or dependent, I'll convert the vector equation into a system of equations.

$$ \begin{cases} 3a_1+a_2+2a_3=0 \\ a_1+4a_2 +a_3 = 0 \end{cases} $$

Then, I'll check if there's a non-trivial solution, that is, different from the null vector of coefficients.

However, it's futile in this case since the system has 3 variables and only 2 equations.

Thus, according to the Rouché-Capelli theorem, the linear system has infinite solutions beyond the trivial null vector solution.tion

Therefore, the three vectors are linearly dependent.

This means one of the three vectors can be obtained as a linear combination of the other two.

Example 3

In a vector space V=R³ over the field K=R, consider two vectors:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} $$

I need to determine if they are linearly dependent.

By definition, vectors are linearly dependent if their linear combination equals zero, with the coefficients α not all being zero simultaneously.

$$ α_1 \cdot v_1 + α_2 \cdot v_2 = 0 $$ $$ α_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + α_2 \cdot \begin{pmatrix} 3 \\ 2 \\ 3 \end{pmatrix} = 0 $$ $$ ( α_1, 2α_1, -α_1 ) + ( 3α_2, 2α_2, 3α_2) = 0 $$

I can represent these vectors as a linear system with three equations and two unknown variables:

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 2α_2 = 0 \\ -α_1 + 3α_2 = 0 \end{cases} $$

I solve the system to check if there is a non-trivial solution (where α₁≠0, α₂≠0)

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 2α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} (- 3α_2) + 3α_2 = 0 \\ 2(- 3α_2) + 2α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ -4α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

The system has no solutions other than the trivial one (α₁=0, α₂=0)

Therefore, vectors v₁ and v₂ are not linearly dependent.

They are linearly independent.

Example 4

In the same vector space V=R³ over the field K=R, consider two other vectors:

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} $$

They are linearly dependent if their linear combination equals zero, with the coefficients α not all being zero simultaneously.

$$ α_1 \cdot v_1 + α_2 \cdot v_2 = 0 $$ $$ α_1 \cdot \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + α_2 \cdot \begin{pmatrix} 3 \\ 6 \\ 3 \end{pmatrix} = 0 $$ $$ ( α_1, 2α_1, -α_1 ) + ( 3α_2, 6α_2, 3α_2) = 0 $$

I express these vectors as a linear system with three equations and two unknowns:

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 6α_2 = 0 \\ -α_1 + 3α_2 = 0 \end{cases} $$

Next, I solve the system:

$$ \begin{cases} α_1 + 3α_2 = 0 \\ 2α_1 + 6α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} (- 3α_2) + 3α_2 = 0 \\ 2(- 3α_2) + 6α_2 = 0 \\ α_1 = - 3α_2 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ 0 = 0 \\ α_1 = - 3α_2 \end{cases} $$

The system has a non-trivial solution.

Hence, vectors v₁ and v₂ are linearly dependent.

Example 5

Given 3 vectors in the vector space V=R³

$$ v_1 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$

$$ v_3 = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Their linear combination equal to the null vector is

$$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} = \vec{0} $$

$$ a_1 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} + a_2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} + a_3 \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

$$ \begin{pmatrix} 3a_1 \\ a_1 \\ -2a_1 \end{pmatrix} + \begin{pmatrix} 2a_2 \\ -a_2 \\ 0 \end{pmatrix} + \begin{pmatrix} a_3 \\ -3a_3 \\ 2a_3 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} $$

Converting the vector equation into a system of Cartesian equations.

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ -2a_1 + 2a_3 = 0 \end{cases} $$

Looking for solutions using the substitution method.

Isolating variable a₁ in the third equation and substituting it into the other equations.

$$ \begin{cases} 3a_1 + 2a_2 + a_3 = 0 \\ a_1 - a_2 - 3a_3 = 0 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 3a_3 + 2a_2 + a_3 = 0 \\ a_3 - a_2 - 3a_3 = 0 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ -a_2 - 2a_3 = 0 \\ a_1 = a_3 \end{cases} $$

Isolating variable a₂ in the second equation and substituting it into the other equations.

$$ \begin{cases} 4a_3 + 2a_2 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 + 2(-2a_3) = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 4a_3 -4a_3 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

$$ \begin{cases} 0 = 0 \\ a_2 = -2a_3 \\ a_1 = a_3 \end{cases} $$

Thus, the system has infinite solutions as a₃ can take any value, determining a₁ and a₂.

Consequently, the vectors v₁, v₂, v₃ are linearly dependent on each other.

This means one of the three vectors can be obtained as a linear combination of the other two vectors.

Note. Observing the three vectors, it's evident that vector v₃ can be derived as a linear combination of v₂ and v₃ $$ \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = 2 \cdot \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} - v_3 $$ $$ v_1 = 2v_2 - \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Geometrically, this means the three linearly dependent vectors v₁, v₂, v₃ lie i/math/bordered-matrix-theoremn the same plane in three-dimensional space.

 

The Demonstration

The vectors v₁,...,v_m are linearly dependent if their linear combination equals the zero vector, with scalar coefficients α₁,...,α_m not all zero.

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = \vec{0} $$

Assuming the scalar coefficient α₁ is non-zero,

$$ a_1 \ne 0 $$

Highlighting vector v₁ by moving all other vectors to the right side,

$$ α_1 \cdot \vec{v}_1 = - α_2 \cdot \vec{v}_2 ... - α_m \cdot \vec{v}_m $$

Knowing α₁ is non-zero, I divide both sides of the equation by α₁

$$ (\frac{1}{α_1}) \cdot α_1 \cdot \vec{v}_1 = (\frac{1}{α_1}) \cdot ( - α_2 \cdot \vec{v}_2 ... - α_m \cdot \vec{v}_m ) $$

$$ \vec{v}_1 = - \frac {α_2 } {α_1} \cdot \vec{v}_2 ... - \frac {α_m} {α_1} \cdot \vec{v}_m $$

For simplicity, I represent the ratios between the scalars with the letter beta (β)

$$ b_2 = - \frac {α_2 } {α_1} \\ b_3 = - \frac {α_3 } {α_1} \\ \vdots \\ b_m = - \frac {α_m } {α_1} $$

And thus, I obtain the expression I wanted to demonstrate.

$$ \vec{v}_1 = β_2 \cdot \vec{v}_2 + ... + β_m \cdot \vec{v}_m $$

Note: The beta coefficients are the ratios $$ β_2 = - \frac {α_2 } {α_1} $$ $$ ... $$ $$ β_m = - \frac {α_m } {α_1} $$

Now, I demonstrate the converse: if vector v₁ is obtained from the linear combination of the remaining vectors,

$$ \vec{v}_1 = β_2 \cdot \vec{v}_2 + ... + β_m \cdot \vec{v}_m $$

then the vectors v₁,v₂,...,v_m are linearly dependent.

$$ - \vec{v}_1 + β_2 \cdot \vec{v}_2 + ... + β_m \cdot \vec{v}_m = \vec{0} $$

If, hypothetically, the scalar coefficients α₂=0, ...., α_m=0 are zero, then the β₂ ... β_m coefficients are also zero.

$$ - \vec{v}_1 + 0 \cdot \vec{v}_2 + ... + 0 \cdot \vec{v}_m
< = \vec{0} $$

Hence, the linear combination reduces to

$$ - \vec{v}_1= \vec{0} $$

This isn't a trivial linear combination, as the coefficient of vector v₁ is non-zero (β=-1) by the initial hypothesis.

Therefore, the linear combination is non-trivial.

Corollary 1

If v₁,...,v_m are linearly dependent vectors, then every subset of vectors is also linearly dependent.

Proof

Starting with the initial assumption α₁=1.

Thus, the following linear combination is non-trivial, and the vectors are linearly dependent.

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = 0 $$

If α_m=0, I can eliminate the last term of the linear combination.

$$ α_1 \cdot \vec{v}_1 + ... + α_{m-1} \cdot \vec{v}_{m-1} + 0 \cdot \vec{v}_m = 0 $$

$$ α_1 \cdot \vec{v}_1 + ... + α_{m-1} \cdot \vec{v}_{m-1} = 0 $$

Knowing α₁ is non-zero by the initial assumption, this last subset of the linear combination is also non-trivial.

Corollary 2

If v₁,...,v_m are linearly dependent vectors, then any set of vectors { v₁,...,v_m+k } including them is linearly dependent, setting the coefficients α_m=0,...,α_m+k=0 to zero.

Proof

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m + ( α_{m+1} \cdot \vec{v}_{m+1} + ... + α_{m+k} \cdot \vec{v}_{m+k} ) = 0 $$

$$ with \: α_{m+1} = 0 \; , \; .... \; , \; α_{m+k} = 0 $$

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m + ( 0 \cdot \vec{v}_{m+1} + ... + 0\cdot \vec{v}_{m+k} ) = 0 $$

$$ α_1 \cdot \vec{v}_1 + ... + α_m \cdot \vec{v}_m = 0 $$

How to Determine Linear Dependence Using Matrix Rank

To check for linear dependence or independence of numerical vectors, one effective method is to observe the rank of the matrix within the equation system.

A set of n numerical vectors v₁, ..., v_n is linearly independent if the row rank of the matrix M_m,n(R) equals n.
$$ r_k = n $$

The column rank of a matrix M(R) refers to the maximum number of independent columns, considering the columns as numerical vectors with n elements.

• If r_k=n, the columns are linearly independent
• If r_k<n, the columns are linearly dependent

When the columns are linearly dependent (r_k < n), it's still possible to find a subset of independent vectors among the non-zero complementary minors of the matrix.

Vectors included in a complementary minor with a non-zero determinant are independent.

Note. The same principle applies when using rows instead of columns, considering rows as numerical vectors. In a matrix M_m,n(R), the matrix rank coincides with both the row and column ranks.

A Practical Example

In a vector space V=R⁴ with field K=R, consider four vectors:

$$ v_1 = ( 1, 0, 1, 2 ) $$ $$ v_2 = ( 1, 3, 0, 0 ) $$ $$ v_3 = ( 1, -3, 2, 4 ) $$ $$ v_4 = ( 2, 3, 1, 2 ) $$

The linear combination of these vectors is as follows:

$$ α_1 \cdot v_1 + α_2 \cdot v_2 + α_3 \cdot v_3 + α_4 \cdot v_4 $$

$$ α_1 \cdot ( 1, 0, 1, 2 ) + α_2 \cdot ( 1, 3, 0, 0 ) + α_3 \cdot ( 1, -3, 2, 4 ) + α_4 \cdot ( 2, 3, 1, 2 ) $$

Arrange these numerical vectors in a column to form a 4x4 square matrix:

$$ M_{4,4} \begin{bmatrix} 1 & 0 & 1 & 2 \\ 1 & 3 & 0 & 0 \\ 1 & -3 & 2 & 4 \\ 2 & 3 & 1 & 2 \\ \end{bmatrix} $$

Then, calculate the determinant of M_{4,4}.

$$ \bigtriangleup M = 0 $$

The matrix has a zero determinant, indicating a rank r_k less than 4.

To determine the matrix rank, use the bordered determinant theorem.

Take a second-order complementary minor with a non-zero determinant.

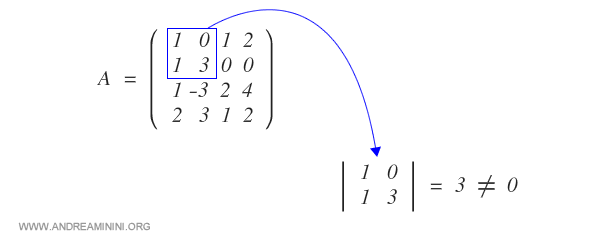
This suggests that the matrix has a rank of at least 2.

To check if the matrix has a rank of 3, verify if at least one of the bordered minors has a non-zero determinant.

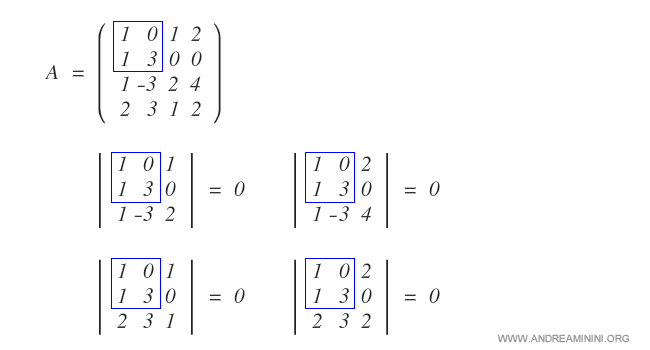
All bordered minors have a zero determinant.

Therefore, according to the bordered determinant theorem, the matrix does not have a rank of 3 or higher.

The matrix has a rank of 2.

Once the matrix rank is calculated, the dependence or independence of the vectors becomes clear.

The matrix consists of n=4 unknowns (columns) but has a rank r_k=2.

$$ r_k \ne n $$

According to the theorem:

1. If r_k=n, the vectors are linearly independent.
2. If r_k≠n, the vectors are linearly dependent.

Thus, the vectors v₁, v₂, v₃, v₄ are linearly dependent.

And to find the independent vectors?

Simply select the vectors in pairs from the complementary minors. Those from a second-order complementary minor with a non-zero determinant are independent of each other.

For example, vectors v₁ and v₂ are independent because they are included in a complementary minor with a non-zero determinant.

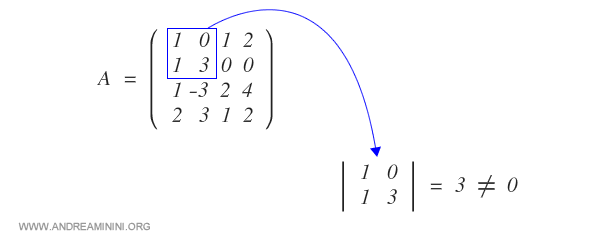
In this case, the matrix rank (2) matches the number of unknowns (columns) in the complementary minor.

The same calculation can be applied to check the independence relationship between vectors v₂ and v₃, v₃ and v₄, v₂ and v₄, v₁ and v₃, v₁ and v₄.

Gauss's Elimination Algorithm

The linear dependence of vectors can also be determined using the rank of a matrix, which can be calculated with the Gauss-Jordan elimination algorithm.

According to Gauss, the number of pivots in a matrix equals its rank.

Example

In the previous exercise, four vectors are arranged as columns in a 4x4 matrix.

$$ M_{4,4} \begin{bmatrix} 1 & 1 & 1 & 2 \\ 0 & 3 & -3 & 3 \\ 1 & 0 & 2 & 1 \\ 2 & 0 & 4 & 2 \\ \end{bmatrix} $$

Then, I transform the matrix into a staircase matrix using Gauss's rules.

$$ M_{4,4} \begin{bmatrix} 1 & 0 & 2 & 1 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} $$

Note. To keep the explanation concise, I will not detail every step of transforming the matrix into a staircase matrix using the Gauss-Jordan algorithm. To see in detail, click here.

The matrix has two steps (pivots), giving it a rank of two (r_k = 2).

Therefore, the vectors v₁, v₂, v₃, and v₄ are linearly dependent because r_k < n.

The two vectors v₁, v₂, where the pivots are located, are linearly independent of each other.

Note. The staircase matrix is only used for calculating the rank. The original vector elements remain the same, i.e., v₁ = ( 1, 1, 1, 2 ), v₂ = ( 0, 3, -3, 3 ), v₃ = ( 1, 0, 2, 1 ), and v₄ = ( 2, 0, 4, 2 ).

Theorems on the Linear Independence of Vectors

• If a set of vectors {v₁, v₂, ..., v_n} are linearly independent, then none of these vectors is the zero vector $$ \vec{v}_1 \ne \vec{0} \\ \vec{v}_2 \ne \vec{0} \\ \vdots \\ \vec{v}_n \ne \vec{0} $$

  See proof.

• In a finitely generated vector space V, consider a set of generators for V $$ \{ v_1, v_2, ..., v_n \} $$ and a set of linearly independent vectors in V $$ \{ w_1, w_2, ..., w_p \} $$, then $$ p \le n $$

  In essence, the number of linearly independent vectors in V is always less than or equal to the number of vectors in a set of generators for V.
  
  See proof

Observations

Some useful notes on vector linear dependency and independence.

• The zero vector is linearly dependent
  According to the definition, a vector is linearly independent if it equals the zero vector only when all coefficients of the linear combination are zero (the trivial solution α=0). $$ \alpha \cdot \vec{v} = \vec{0} $$ The zero vector equals itself (the zero vector) even when the scalar coefficient α of the linear combination is not zero (α≠0). $$ \alpha \cdot \vec{0} = \vec{0} $$ Therefore, the zero vector is always linearly dependent.

And so on.