Gauss' Method of Elimination

Gauss' method of elimination determines the possible solution set of a linear system.

Note: Conventionally, Gauss' method is applied to the rows of the matrix. However, it can also be applied to columns. Therefore, in certain practical situations, calculations can be made using columns instead of rows.

It's also known as the Gauss-Jordan elimination method, although the latter is a variant of Gauss' elimination method.

What's its purpose?

Gauss' elimination method transforms a system of linear equations into a staircase system.

This significantly simplifies the calculation of the rank and the finding of solutions for the linear system, especially when it consists of numerous equations and variables.

How Gauss' Method of Elimination Works

This method aims to find an equivalent matrix that is easier to analyze.

What is an equivalent matrix? It's a matrix whose associated linear systems are equivalent. Thus, the linear system associated with the equivalent matrix M' has the same solutions as the system associated with the original matrix M but is simpler to analyze.

The Gauss-Jordan elimination process involves reducing the initial matrix to a staircase matrix (or step matrix).

Each nonzero step in the staircase is called a pivot.

Note: The pivot is the first nonzero element from the left in a nonzero row. It's also known as the leading term.

Characteristics of a Staircase Matrix

A staircase matrix has the following characteristics:

1. Null rows are at the bottom
   
   

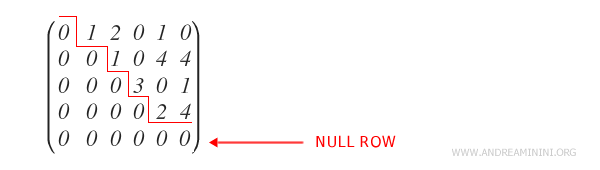
   What's a null row? A null row refers to a row with all elements equal to zero.

2. The pivot of each nonzero row is in a column to the right of the pivots in the previous rows.
   

To build the staircase of the equivalent matrix, certain permissible transformation operations called "Gauss' moves" can be performed.

What are Gauss' Moves?

The permissible operations on the matrix, according to Gauss, are:

1. Swapping one row with another
   
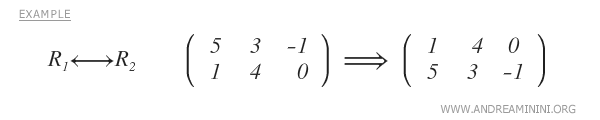
2. Multiplying a row by a non-zero real number
   
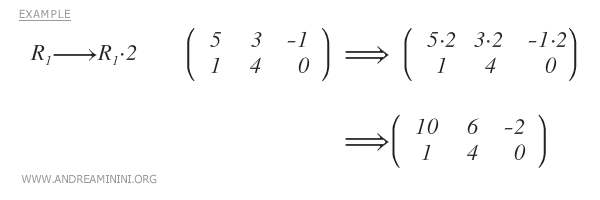
3. Adding two rows together
   

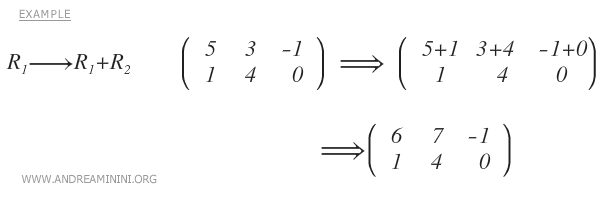
Note: It's also possible to combine the last two operations into one, i.e., adding to a row the multiple of another row.

Gauss' Algorithm

Given a matrix A with m rows and n columns, the objective is to calculate an equivalent matrix in staircase form.

Note. If the matrix is null, the algorithm concludes immediately.

Step 1

Identify the first non-zero column j of A from the left.

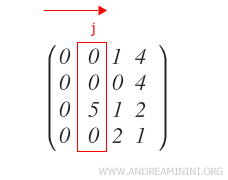
If the first element of column j is non-zero, proceed to step 2.

Otherwise, if it is zero, find the first row Rx that has a non-zero j-th element

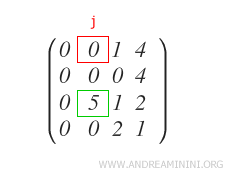
Then, swap row R₁ with row R_x and move to step 2.

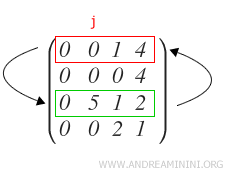
Note. The notation for indicating this row swapping operation is as follows:

This way, the first pivot (p₁) of the matrix is obtained.

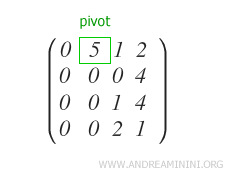
Step 2

Ensure that the other q_j-th elements of the rows R_i below the pivot are all zero.

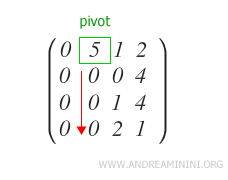
If not, and some elements are non-zero, apply the following subtraction to row R_i.

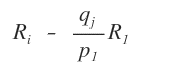
This method helps eliminate any non-zero elements below the pivot.

Once the last row is reached, move to step 3.

Step 3

Identify the first j-th column to the right of the last pivot that does not have all zeros in the rows below the pivot.

If such a column does not exist, the algorithm ends here.

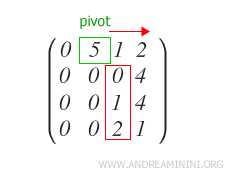
In this case, the column exists.

The first element of the column is a zero. Therefore, find the first underlying row with a non-zero value and swap the rows.

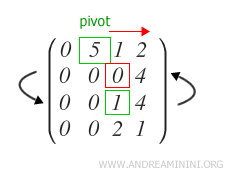
This way, the second pivot p₂ of the staircase matrix is found.

If the pivot is on the last row of the matrix (m), the algorithm ends here.

In this case, we are only at the second row (R₂) out of four, so the process continues to step 4.

Step 4

Verify that the other q_j-th elements of the rows R_i below the last pivot p_k are all zero.

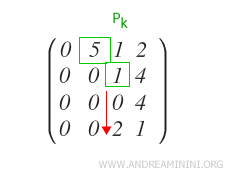
In this case, a non-zero element is found in row R_i (i=4).

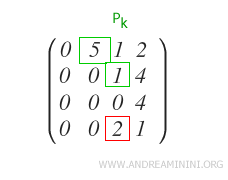
To eliminate it, apply the following subtraction to row R_i.

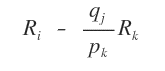
Apply the formula to all elements of the row.

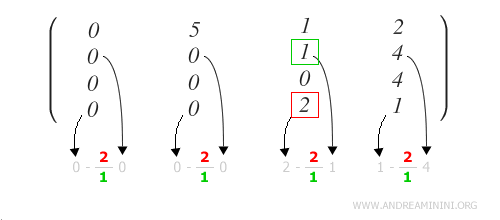
Note. It's unnecessary to apply it to the first elements of the row, as it automatically cancels out with the zeros of the pivot row. For clarity, however, I have chosen to apply it across the entire row.

Once the calculations are done, the following situation is obtained.

This results in a staircase matrix.

And so on.