Linear Systems in Row Echelon Form

A linear system is said to be in row echelon form when its equations appear in a structured, descending pattern.

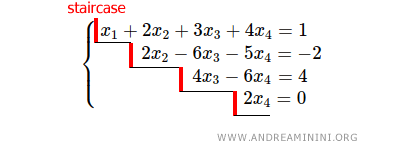
In such systems, each successive equation involves fewer leading variables than the one above it, creating a clear downward progression.

The number of pivot rows in the system matches the rank of its matrix.

This structure makes it remarkably easy to determine the rank, even for large systems with many variables.

Why are systems in row echelon form so useful?

They are exceptionally convenient to solve. Once a system has been arranged in row echelon form, its unknowns can be computed by straightforward back-substitution, starting from the final equation.

If a system is not already in this form, it can be transformed using Gauss - Jordan elimination.

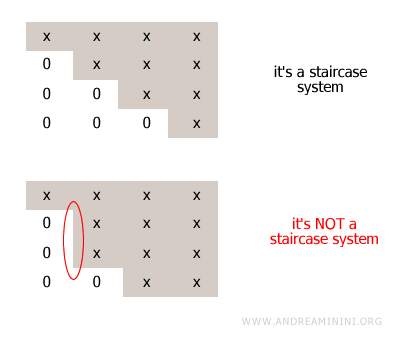
Note. A proper echelon form requires that each leading entry be strictly to the right of the leading entry in the row above. If leading entries skip rows or appear misaligned, the matrix is not in row echelon form.

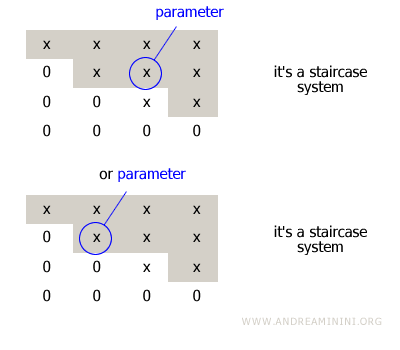
When a leading entry spans more than one column, the extra variables must be treated as free parameters of the system.

A Practical Example

Example 1

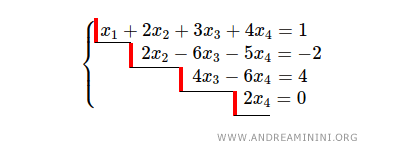
This linear system is already in row echelon form:

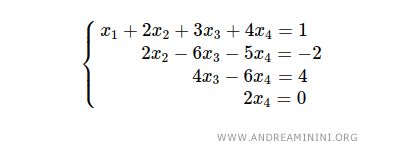
The system contains four pivot rows, and there are n=4 variables.

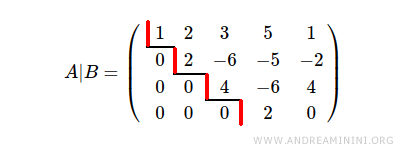
The augmented matrix has rank r=4, as each pivot row contributes one to the rank.

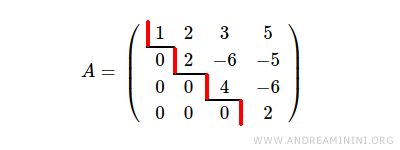
The coefficient matrix also has rank 4, for the same reason.

By the Rouché - Capelli Theorem, the system is consistent and admits at least one solution.

Since the rank equals the number of variables (r=n=4), the solution is unique.

$$ \infty^{n-r} = \infty^{4-4} = \infty^0 = 1 $$

Solving proceeds naturally from the final equation: 2x₄=0 gives x₄=0.

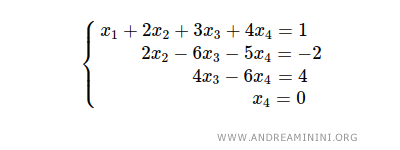
Substituting x₄=0 into the third equation yields 4x₃=4, so x₃=1.

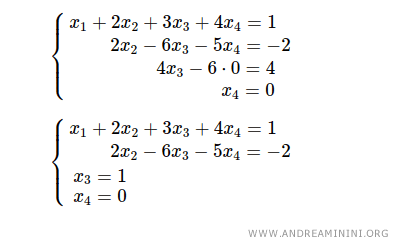
Next, substituting x₃=1 and x₄=0 into the second equation gives 2x₂-6·1=-2, hence x₂=2.

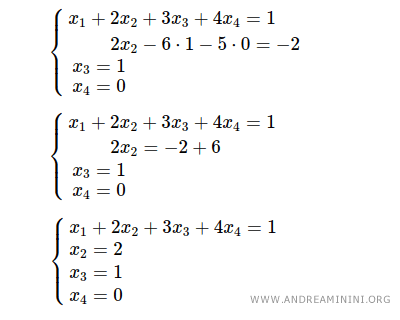
Finally, substituting x₂=2, x₃=1 and x₄=0 into the first equation yields x₁=-6.

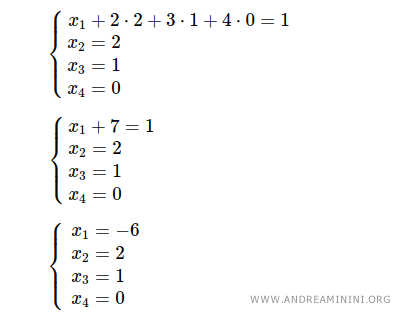
The system is thus solved. Its unique solution is x₁=-6, x₂=2, x₃=1 and x₄=0.

Note. This example illustrates why reducing a system to row echelon form is so powerful. It turns a potentially complex system into one that can be solved immediately by back-substitution.

Example 2

This system is also in echelon form:

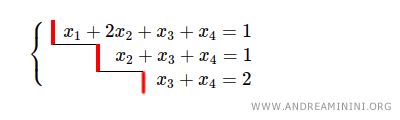
The augmented matrix has rank r=3, corresponding to its three pivot rows.

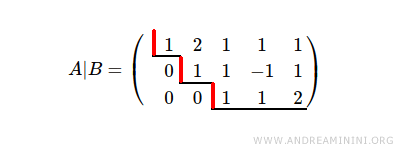
The coefficient matrix also has rank r=3.

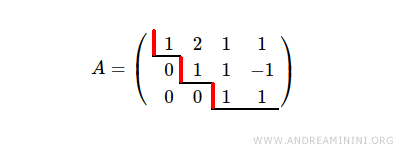
By the Rouché - Capelli Theorem, the system may have a unique solution or infinitely many.

Here, since r=3<4=n, the solution set is infinite.

$$ \infty^{n-r} = \infty^{4-3} = \infty^1 = \infty $$

To describe all solutions, I introduce a free parameter.

From the last equation, I express x₃ in terms of x₄:

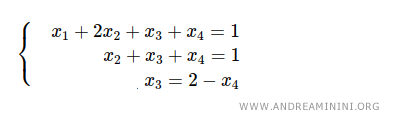
Substituting x₃=2-x₄ into the second equation yields x₂=-1.

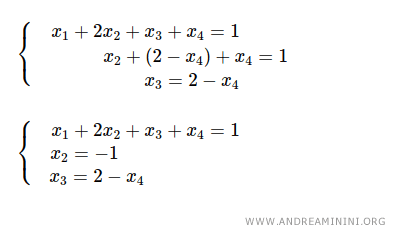
Substituting x₂=-1 and x₃=2-x₄ into the first equation yields x₁=1.

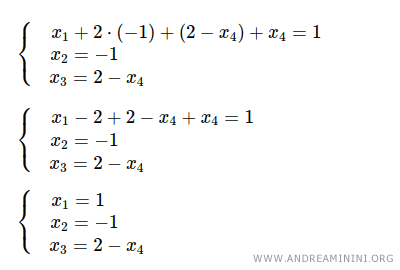
Thus the general solution is

$$ \begin{cases} x_1 = 1 \\ x_2 = -1 \\ x_3 = 2 - k \end{cases} $$

with free parameter k = x₄ ∈ ℝ. The system therefore has infinitely many solutions.

Observations

Some useful facts about row echelon form:

• Every matrix in row echelon form is upper triangular, but the reverse is not true. Upper triangularity alone does not guarantee the systematic placement of leading entries required by echelon form.
• The determinant of a square echelon matrix is simply the product of its diagonal entries. Because the matrix is triangular, the determinant calculation reduces to multiplying the diagonal terms, making the computation particularly efficient.

And so on.