Flux of a Vector Field

What is the flux of a vector field?

The flux of a vector field V through a surface S in space is a scalar quantity defined by the surface integral of the dot product v·ds, evaluated point by point across S: $$ Φ_S = \int_S \vec{v} \cdot \vec{ds} $$

Here, $\vec{v}$ represents the vectors of the field V, while $\vec{ds}$ represents infinitesimal outward-pointing normal vectors perpendicular to each surface element of S.

The dot product $\vec{v} \cdot \vec{ds}$ at any point s on the surface is referred to as the local flux contribution.

$$ \vec{v} \cdot \vec{ds} $$

The sum of these local contributions over the entire surface S defines the total flux of the vector field through S:

$$ Φ_S = \int_S \vec{v} \cdot \vec{ds} $$

Note: The surface S can be either open or closed. For an open surface, the orientation of the normal vector can be chosen arbitrarily; flux is considered positive when directed outward, and negative when directed inward. For a closed surface, the normal vectors are conventionally oriented outward. The flux through a closed surface is denoted using a surface integral with a circle: $$ Φ_S = \oint_S \vec{v} \cdot \vec{ds} $$

A practical example

Let’s consider a closed, curved surface S.

example of a closed surface

We divide the surface into infinitesimal elements s.

This allows us to treat each small element locally as a flat patch.

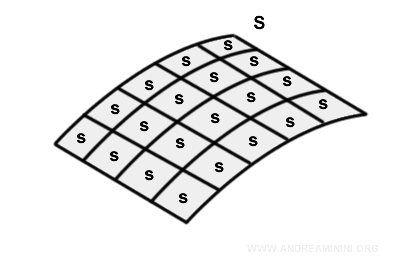
dividing surface S into infinitesimal elements s

At each point s, we draw the outward normal vector $\vec{ds}$, whose magnitude equals the area of the corresponding surface element.

A normal vector is perpendicular to the local tangent plane - that is, it forms a 90° angle with the surface at that point.

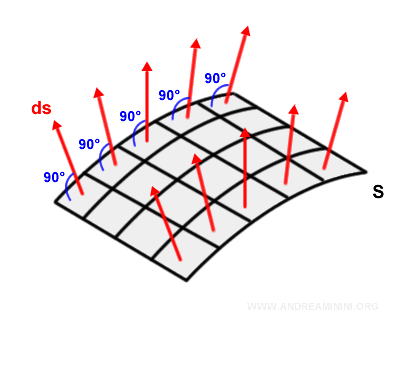
normal vectors to the surface elements

Note: If the surface S were flat, all the normal vectors would point in the same direction. The underlying concept remains the same.
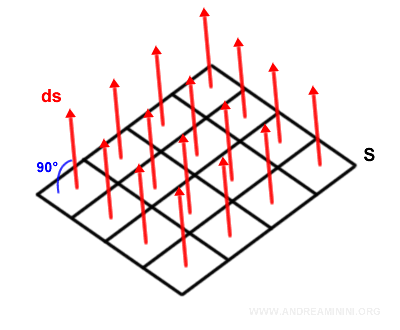
case of a flat surface

Now we introduce a vector field V - for example, an electric or magnetic field.

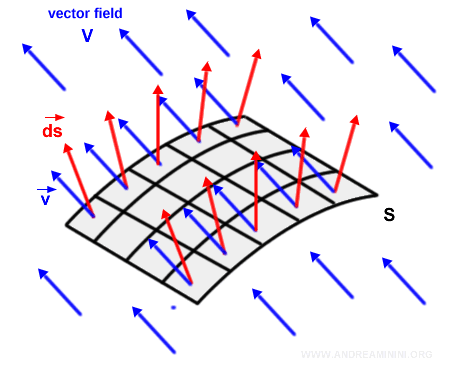
vector field applied to the surface

Note: For clarity, the illustration shows a constant vector field, where all vectors have the same direction, magnitude, and orientation. The same reasoning applies to more complex fields with varying directions, magnitudes, and orientations.
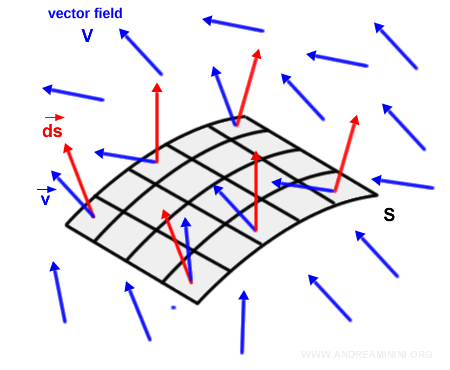
example of a more complex vector field

For each surface element s, we compute the dot product between the field vector $\vec{v}$ and the normal vector $\vec{ds}$.

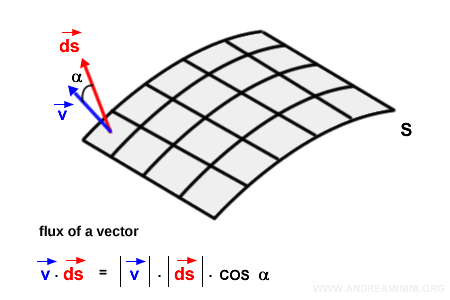
The dot product of two vectors is equal to the product of their magnitudes $|\vec{v}| \cdot |\vec{ds}|$ times the cosine of the angle $\alpha$ between them:

$$ \vec{v} \cdot \vec{ds} = |\vec{v}| \cdot |\vec{ds}| \cdot \cos \alpha $$

The flux contribution at each surface element s is this local dot product.

dot product between vector v and ds

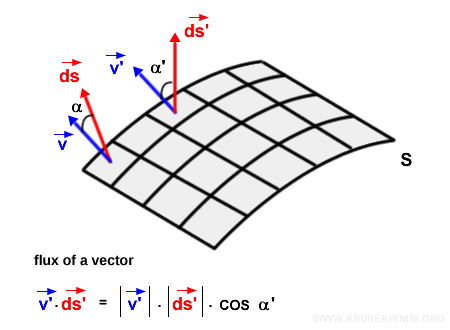
This process is repeated for every surface element $\vec{ds}$.

The value of $\vec{v} \cdot \vec{ds}$ varies from point to point, as the angle between the field vector and the normal vector changes across the surface.

computing flux at each surface element ds

Note: In more complex vector fields, both the direction and the magnitude of the field vectors may vary. These variations further affect the value of the dot product at each point.
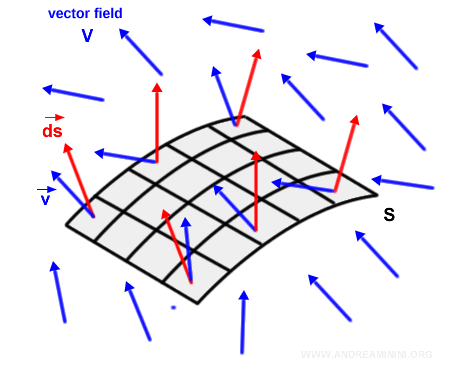
example of a more complex vector field

The sum of all flux contributions across surface S yields the total flux of the vector field.

Because this is a sum over infinitesimal elements, we express it as an integral:

$$ Φ_S = \int_S \vec{v} \cdot \vec{ds} $$

Note: If S encloses a solid, the flux of the vector field must be computed for each face of the solid’s boundary. The procedure is the same in each case. For example, if the solid is a cube or rectangular prism, you compute the flux for each of its six faces individually.
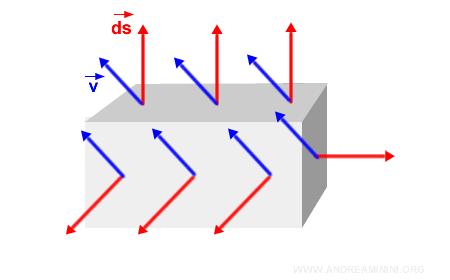
example of a rectangular prism

And so on.