Scalar Multiplication of a Vector

When I multiply a vector v by a scalar, denoted as k, I'm scaling each component of the vector by that scalar. This operation can be represented as:

$$ k \cdot \vec{v} = k \cdot \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} = \begin{pmatrix} k \cdot v_1 \\ k \cdot v_2 \\ \vdots \\ k \cdot v_n \end{pmatrix} $$

Here, a "scalar" refers to a single numerical value.

Multiplying a vector v by a scalar k results in a new vector w = k · v that:

Points in the same direction as v when k is positive.
Has a magnitude equal to |k| times the magnitude of v.
Reverses direction if k is negative.

Note: If k = 0, the result is a null vector, effectively "zeroing out" v. When k = 1, the vector remains unchanged, and when k = -1, the vector flips to -v.

Practical Example

Consider a vector v in three-dimensional space (x, y, z):

$$ \vec{v} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

Multiplying this vector by a scalar k = 2 yields:

$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

The resulting vector is:

$$ k \cdot \vec{v} = 2 \cdot \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 6 \\ 2 \\ -4 \end{pmatrix} $$

Example 2

For a vector v with a magnitude |v| = 3 and a scalar k = 2:

example

The resulting vector w has the same direction as v but a magnitude of 6:

$$ \vec{w} = |k| \cdot \vec{v} $$

$$ | \vec{w} | = |k| \cdot | \vec{v} | = 2 \cdot 3 = 6 $$

This relationship is illustrated visually below.

example

Note: Multiplying a vector by a scalar k scales each of its components. For example, with k = 3 and v = (1,2)^T:

$$ k \cdot \vec{v} = 3 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \end{pmatrix} $$

This transformation can also be visualized.
example

Example 3

For a vector v with magnitude |v| = 3 and a negative scalar k = -2:

example

The resulting vector w points in the opposite direction to v and has a magnitude of 6:

$$ | \vec{w} | = |k| \cdot | \vec{v} | = |-2| \cdot 3 = 6 $$

This change in direction and magnitude can also be represented visually.

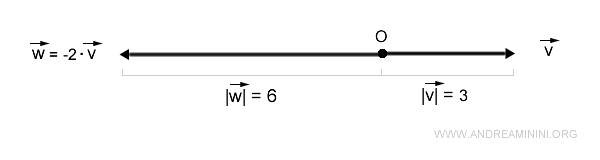
example

Note: When k = -1, the result is -v, a vector with the same magnitude as v but in the opposite direction.