Vector Representation of a Line

A geometric vector identifies a direction shared by all lines in the plane parallel to the vector.

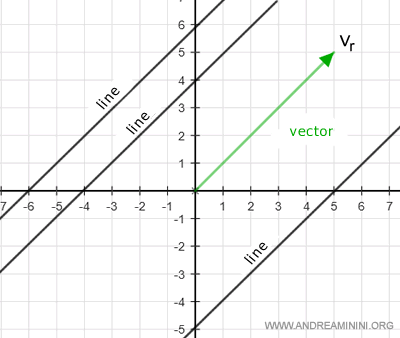
Therefore, any line in the plane can be described by:

• a non-trivial geometric vector v_r, known as the direction vector, which indicates the line's direction $$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$

  The parameters l and m are the line's directional parameters.

• a generic point P₀ on the plane through which the line passes. $$ P_0 = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

  Example
  

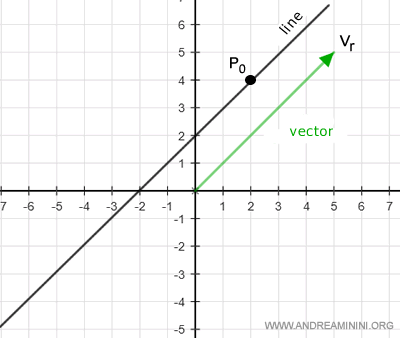
A generic point on the plane belongs to the line if there exists a scalar alpha in R such that

$$ OP = OP_0 + \alpha v_r $$

Example

The point P₁ has coordinates (-5,-3).

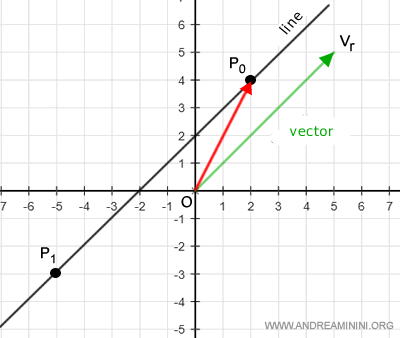
Point P₁ belongs to the line if

$$ OP_1 = OP_0 + \alpha v_r $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \alpha \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

Solving the system of equations to check for a scalar alpha

$$ \begin{cases} -5 = 2 + \alpha 5 \\ -3 = 4 + \alpha 5 \end{cases} = \begin{cases} \alpha = - \frac{7}{5} \\ \alpha = - \frac{7}{5} \end{cases} $$

The system resolves with the scalar alpha -7/5

Indeed

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \alpha \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5 \cdot ( - \frac{7}{5} ) \\ 5 \cdot ( - \frac{7}{5} ) \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 - 7 \\ 4 - 7 \end{pmatrix} $$

$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \end{pmatrix} $$

We can generalize this result by stating that

All coordinates of all points on the line are characterized by the following equation, called the vector equation of the line: $$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \alpha \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$Transforming the vector equation into a system of equations, we get the parametric equations of the line:$$ \begin{cases} x = x_0 + \alpha l \\ y = y_0 + \alpha m \end{cases} $$

There are infinite vector and parametric equations because there are infinite multiples of the direction vector.

Cartesian Equations

The vector P₀P₁ is parallel to the direction vector vr.

According to theory, a vector is parallel and proportional to another if

$$ \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} \le 1 $$

This is verified if

$$ det \begin{pmatrix} x-x_0 & l \\ y - y_0 & m \end{pmatrix} = 0 $$

which, upon calculating the determinant, becomes

$$ m ( x-x_0 ) - l ( y - y_0 ) = 0 $$

This results in the Cartesian equation.

Again, there are infinite Cartesian equations.