Axial Vectors (Pseudovectors)

An axial vector, also known as a pseudovector, is a vector quantity that remains unchanged under a spatial reflection, that is, under a parity transformation.

Axial vectors transform in the same way as ordinary vectors under rotations, but they behave differently when the spatial coordinates are inverted through a parity transformation (see parity operator).

In other words, under a parity transformation, an ordinary (or polar) vector reverses its direction, whereas an axial vector does not.

To clearly understand the distinction between an ordinary vector and an axial vector, it is helpful to examine a concrete example.

A practical example

Example of an ordinary vector

Consider an ordinary vector $ \vec v $.

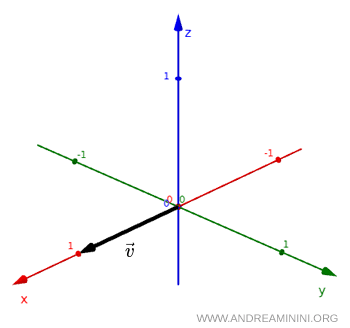
If we perform a spatial inversion, that is $ x \to -x $ and $ y \to -y $, the vector is transformed into its opposite vector $ - \vec v $.

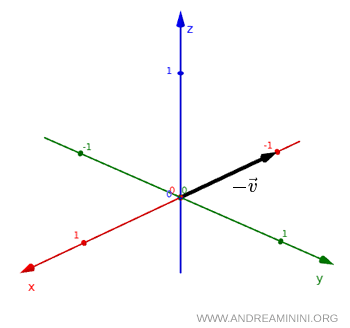
The new vector $ - \vec v $ has the same magnitude and spatial direction, but its orientation is reversed relative to the original vector $ \vec v $.

In other words, the vector changes sign under a spatial inversion.

This means that when an ordinary vector is observed in a mirrored coordinate system, its magnitude remains unchanged while its orientation is reversed.

Note. Typical examples of ordinary vectors in physics include displacement, velocity, and force.

By contrast, an axial vector remains invariant under a spatial reflection.

Example of an axial vector

A canonical example of an axial vector is angular momentum.

If we consider a position vector $ \vec r $ and a momentum vector $ \vec p $, the angular momentum is defined as their cross product:

$$ \vec L = \vec r \times \vec p $$

In general, the cross product of two polar vectors always produces an axial vector.

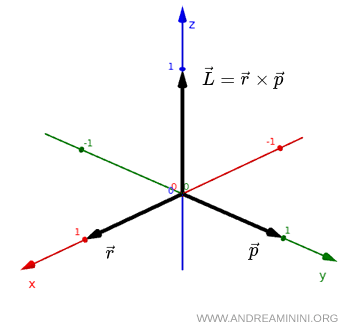
If the system is observed in a mirror, the vectors $ \vec r $ and $ \vec p $ transform into $ - \vec r $ and $ - \vec p $, respectively. However, their cross product retains the same orientation.

$$ \vec L = \vec r \times \vec p = ( - \vec r ) \times ( - \vec p ) $$

In both cases, the vector $ \vec L $ is perpendicular to the plane defined by $ \vec r $ and $ \vec p $, and it points in the same direction along the $ z $ axis.

 

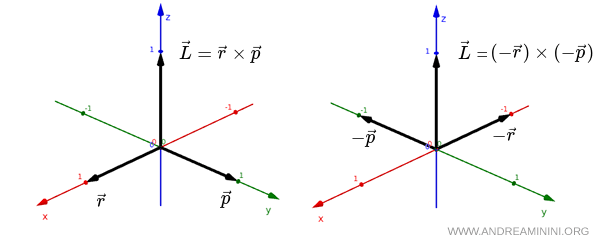
Therefore, the axial vector $ \vec L $ does not change sign under a spatial inversion.

Note. Other examples of axial vectors in physics include angular velocity, torque, and the magnetic field. All of these arise from a vector cross product.

What is the physical meaning of axial vectors?

Axial vectors reveal a fundamental property of space: some physical quantities depend not only on direction, but also on the orientation of space itself.

This is why they play a central role in phenomena involving parity, especially in the context of fundamental interactions.

In particular, they are essential for understanding parity violation in the weak interaction.

And so on.