Torque
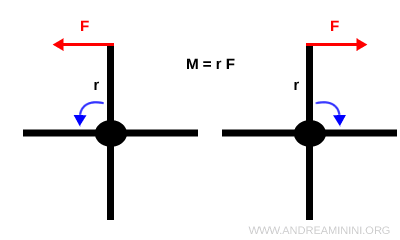
Torque (or moment of a force) describes a force’s ability to make an object rotate about a point or an axis. The fundamental formula is: $$ M = F \cdot d $$ where $F$ is the magnitude of the force and $d$ is the lever arm (or radius)-the perpendicular distance from the line of action of the force to the pivot point (or axis of rotation).
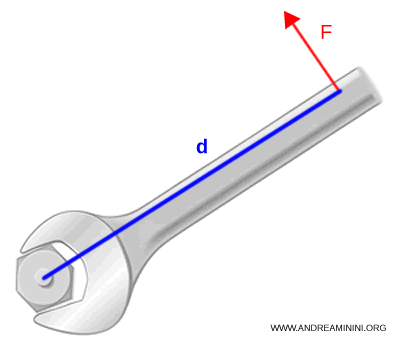
If the force isn’t applied perpendicularly, torque is calculated as: $$ M = F \cdot d \cdot \sin \theta $$ where $\theta$ is the angle between the direction of the force and the lever arm.
So, to determine torque, you need more than just the force-you also need to know where and in which direction the force is applied relative to the axis of rotation.
By convention, torque is taken as
- positive $(M > 0)$ if the rotation is counterclockwise
- negative $(M < 0)$ if the rotation is clockwise
That said, the sign convention can vary depending on the context.
Note. When several torques act simultaneously, the sign of each one is determined by the effect it would produce if acting alone. The net torque is then found as the algebraic sum of all individual torques.
Example
Suppose I use a 0.3 m wrench to loosen a bolt by applying a 20 N force perpendicular to the arm.
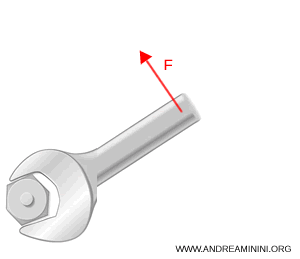
The torque on the bolt is 6 N·m (newton-meters):
$$ M = 20 \times 0.3 = 6 \, \text{N·m} $$
If instead I use a longer wrench, say 0.6 m, while applying the same 20 N force perpendicularly,
$$ M = 20 \times 0.6 = 12 \, \text{N·m} $$
The torque has doubled.
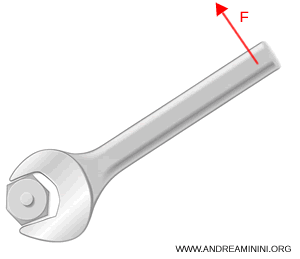
This makes it clear: the farther from the axis the force is applied, the easier it is to turn the bolt.
In plain terms: a longer wrench lets you do the same job with less effort, because it increases torque without increasing force.
Note. The same principle explains why door handles are placed far from the hinges. Pushing close to the hinges requires much more force than pushing at the handle.

For example, applying a 10 N force at 1 meter from the hinges gives a torque of 10 N·m: $$ M = F \times d = 10 \ N \times 1 \ m = 10 \, \text{N·m} $$ But if I push only 0.2 m from the hinges, to get the same torque ($ M = 10 \ N \cdot m $) I’d need five times the force: $$ F = \frac{M}{d} = \frac{10 \ N \cdot m}{0.2 \ m} = 50 \, \text{N} $$
The Torque Formula
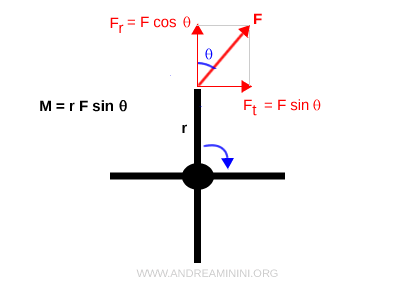
A force $\vec{F}$ applied at a point located a distance $ r $ from the axis of rotation of a rigid body can cause the body to rotate. This rotational effect is measured by the torque $M$, defined as: $$ M = r F \sin \theta $$ where $\theta$ is the angle between the position vector and the direction of the force.
If the force is applied radially-that is, along the radius connecting the point of application to the axis of rotation-the torque is zero: $ M = 0 $.
In this case, no rotation occurs.
By contrast, if the force is applied perpendicular to the radius, torque is maximized because the entire magnitude of the force contributes to the rotation.
In general, only the tangential component of a force produces rotation; the radial component has no effect.
For this reason, torque is calculated by projecting the force onto the tangential direction:
$$ M = r \, (F \sin \theta) $$
The radial component can be disregarded.
Exercises
Exercise 1
Find the torque produced by a force of $ F=40 \ N $ applied at a distance of $ r = 0.20 \ m $ from the axis of rotation, at an angle of 30° relative to the lever arm.
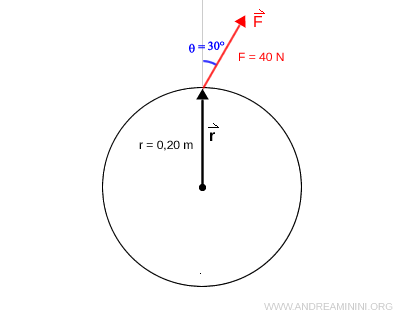
The formula for torque is:
$$ M = r \cdot F \cdot \sin \theta $$
Here, $ r $ is the distance from the axis of rotation-that is, the length of the lever arm $ \vec{r} $. In this case, $ r = 0.20 \ m $.
$$ M = 0.20 \ m \cdot F \cdot \sin \theta $$
The applied force is $ F = 40 \ N $
$$ M = 0.20 \ m \cdot 40 \ N \cdot \sin \theta $$
The angle between the force vector $ \vec{F} $ and the lever arm $ \vec{r} $ is $ \theta = 30° $.
$$ M = 0.20 \ m \cdot 40 \ N \cdot \sin 30° $$
Since $ \sin 30° = \tfrac{1}{2} $,
$$ M = 0.20 \ m \cdot 40 \ N \cdot \tfrac{1}{2} $$
This gives the tangential component of the force: $ F_x = 40 \ N \cdot \tfrac{1}{2} = 20 \ N $
$$ M = 0.20 \ m \cdot 20 \ N $$
Therefore, the torque is 4 newton-meters.
$$ M = 4 \ Nm $$
And so on.
