Moment of a Couple

The moment of a couple is the rotational effect produced by one of the two forces multiplied by the distance between their lines of action. It is calculated using $$ M = F \cdot d $$ where $ F $ is the magnitude of one of the forces and $ d $ is the distance between their lines of action.

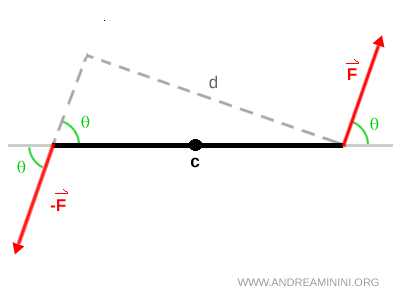
If the forces are not perpendicular to the line connecting their lines of action, the expression becomes $$ M = F \cdot d \cdot \sin\theta $$ where $ \theta $ is the angle between the force and the connecting line.

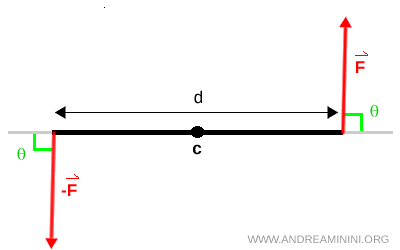
A couple consists of two forces that are equal, parallel and opposite. They produce no linear motion and generate only rotation.

In a couple, the forces have equal magnitude, act along parallel lines, are separated by a fixed distance and point in opposite directions.

The distance between the two lines of action is called the arm of the couple.

Even though the two forces cancel out as a resultant, they still produce a net rotational effect because they act on opposite sides of the object and in opposite directions, without causing any translation.

Note. As with the moment of a single force, the sign convention for a couple is positive ( $ M > 0 $ ) for counterclockwise rotation and negative ( $ M < 0 $ ) for clockwise rotation. If $ M=0 $ there is no rotation of the rigid body.

Example

Consider a hydraulic valve operated with both hands. The left hand pushes downward and the right hand pushes upward with the same force, $ F = 8 \ N $.

Each hand is positioned $ 10 \ cm $ from the center of the valve and applies its force perpendicular to the arm.

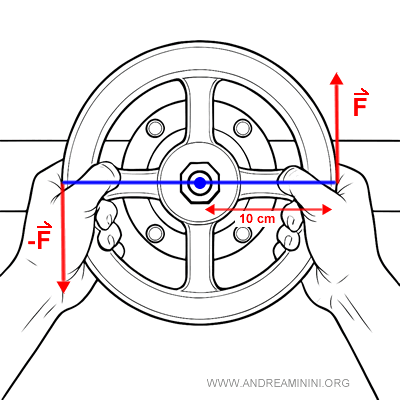
This action generates a couple, producing a rotational effect.

$$ M = F \cdot d $$

The distance between the forces is $ 10 \ cm + 10 \ cm = 20 \ cm $.

$$ M = F \cdot ( 20 \ cm )  $$

Convert to meters.

$$ M = F \cdot ( 0.2 \ m )  $$

We consider only one of the two forces.

$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) $$

$$ M = 1.6 \ Nm $$

The moment of the couple is therefore 1.6 Nm.

Example 2

Now consider the same situation, but the forces are applied at an angle of 110° relative to the arm. How does this affect the moment?

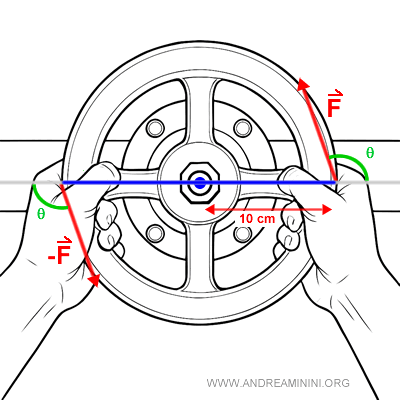
All other values remain the same. Each hand applies a force of $ 8 \ N $ at a distance of $ 10 \ cm $ from the center.

In this case, the moment must take into account the angle $ \theta = 110° $.

$$ M = F \cdot d \cdot \sin\theta $$

$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 110° $$

Since the sine of an angle in the second quadrant can be rewritten using $ \sin \theta = \sin (180° - \theta ) $, it follows that $ \sin 110° = \sin (180° - 110°) = \sin ( 70° ) $

$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 70° $$

$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot 0.94 $$

$$ M \approx 1.50 \ Nm $$

The moment of the couple is slightly lower than in the previous example where the forces acted perpendicular to the diameter of the valve.

And so on.