Levers in physics

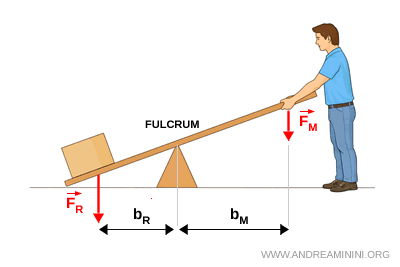
Each force is associated with a lever arm, defined as the perpendicular distance between the fulcrum and the line of action of the force. We denote:

• \( b_M \) as the lever arm of the applied force
• \( b_R \) as the lever arm of the resisting force

The applied force \( F_M \) and the resisting force \( F_R \) are balanced by the reaction force exerted at the fulcrum.

For static equilibrium, the net torque acting on the lever must be zero when the fulcrum is chosen as the axis of rotation.

$$ b_R F_R = b_M F_M $$

This condition shows that the magnitude of a force can be reduced by increasing its lever arm, or increased by shortening it.

For example, when lifting a heavy object, it is advantageous to apply the force \( F_M \) as far from the fulcrum as possible. This increases the lever arm \( b_M \) and reduces the magnitude of the force required.

From a practical standpoint, levers are simple machines that allow forces to be balanced or amplified in order to lift, move, or overcome a resistance.

A practical example

Consider a lever in equilibrium, for which the following relationship holds:

$$ b_R F_R = b_M F_M $$

Assume that the resisting force is

$$ F_R = 100\ \text{N} $$

and that its lever arm is

$$ b_R = 0.20\ \text{m} $$

If the applied force acts at a distance of one meter from the fulcrum, that is $ b_M = 1.00\ \text{m} $, the required applied force is:

$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.20}{1.00} \cdot 100 = 20\ \text{N} $$

The applied force is therefore much smaller than the resisting force.

Note. If the applied force were instead exerted only ten centimeters from the fulcrum, that is $ b_M = 0.10\ \text{m} $, the required applied force would be much larger $$  F_M = \frac{0.20}{0.10} \cdot 100 = 200\ \text{N} $$ In this case, the applied force must exceed the resisting force.

Thus, for a given resisting force, increasing the lever arm of the applied force reduces the force required, whereas decreasing the lever arm increases it.

Advantageous, disadvantageous, and neutral levers

Depending on the relative lengths of the lever arms, a lever may be classified as advantageous, disadvantageous, or neutral.

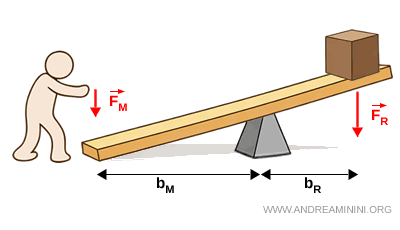
• Advantageous lever
  A lever is advantageous if the lever arm of the applied force is longer than that of the resisting force $$
  b_M > b_R $$ In this case, maintaining equilibrium requires an applied force smaller than the resisting force $$ F_M < F_R $$ The lever therefore makes it possible to overcome a large resisting force by applying a smaller one.
  
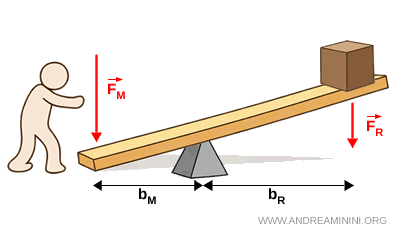
• Disadvantageous lever
  A lever is disadvantageous if the lever arm of the applied force is shorter than that of the resisting force $$ b_M < b_R
  $$ In this case, equilibrium requires an applied force greater than the resisting force $$ F_M > F_R
  $$ The lever does not reduce the required force, but it may be useful when greater precision or higher speed of motion is needed.
  
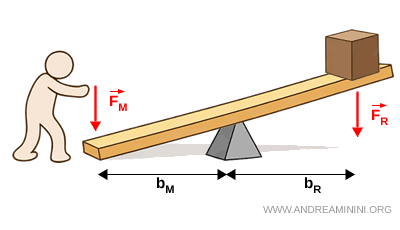
• Neutral lever
  A lever is neutral if the two lever arms are equal $$ b_M = b_R $$ In this case, the applied force equals the resisting force $$ F_M = F_R $$ The lever provides neither mechanical advantage nor mechanical disadvantage in terms of force magnitude.
  

Types of levers

Levers are classified into three types according to the relative positions of the fulcrum, the applied force, and the resisting force.

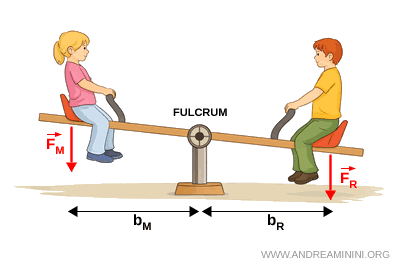
• First-class lever
  The fulcrum lies between the applied force and the resisting force. A first-class lever may be advantageous, disadvantageous, or neutral. Typical examples include scissors and playground seesaws.
  
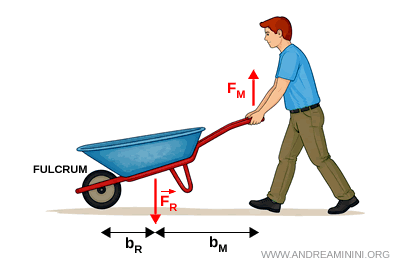
• Second-class lever
  The resisting force lies between the fulcrum and the applied force. This type of lever is always advantageous. Common examples include wheelbarrows, nutcrackers, and bottle openers.
  
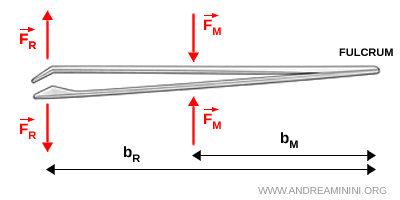
• Third-class lever
• The applied force lies between the fulcrum and the resisting force. This type of lever is always disadvantageous because the lever arm $ b_R $ is longer than the lever arm $ b_M $, but it enables rapid and precise movements. Tweezers are a typical example.
  

These three classes of levers illustrate how the position of the forces is often more important than their magnitude.

By using lever arms appropriately, a small force can overcome a much larger one.

A practical example

A worker uses a rigid lever to lift a crate with a mass of 75 kg.

The crate is located 0.40 m from the fulcrum, while the worker applies the effort force at the opposite end of the lever, 1.60 m from the fulcrum.

The given data are:

• \( b_R = 0.40 \ \text{m} \)
• \( b_M = 1.60 \ \text{m} \)
• \( m = 75 \ \text{kg} \)

What is the magnitude of the resisting force exerted by the crate?

The resisting force is equal to the weight of the crate:

$$ F_R = P = mg $$

The mass is $ m = 75 \ \text{kg} $ and the acceleration due to gravity is \( g = 9.8 \ \text{N/kg} \).

$$ F_R = 75 ( \text{kg} ) \cdot 9.8  ( \text{N/kg} ) = 735 \ \text{N} $$

Therefore, the magnitude of the resisting force acting on the lever is:

$$ F_R = 735 \ \text{N} $$

What effort force must the worker apply to keep the lever in equilibrium?

The condition for static equilibrium of a lever is:

$$ b_R F_R = b_M F_M $$

Solving for \( F_M \):

$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.40}{1.60} \cdot 735 $$

$$ F_M = 0.25 \cdot 735 = 183.75 \ \text{N} \approx 184 \ \text{N} $$

Hence, the effort force required to maintain equilibrium is:

$$ F_M \approx 184 \ \text{N} $$

What type of lever is this?

A lever is said to be mechanically advantageous when \( b_M > b_R \).

In this case, $ b_M = 1.60 \ \text{m} $ and $ b_R = 0.40 \ \text{m} $, so the lever is mechanically advantageous.

The mechanical advantage is therefore:

$$ \frac{F_R}{F_M} = \frac{b_M}{b_R} = \frac{1.60}{0.40} = 4 $$

This means that the effort force is approximately four times smaller than the resisting force.

Exercise 2

A sack with a mass of $ m = 200 \ \text{kg} $ is placed at one end of a first-class lever. At the opposite end, a worker applies an effort force of $ F_M = 200 \ \text{N} $.

At what distance from the sack must the fulcrum be positioned for the lever to remain in static equilibrium?

The equilibrium condition for a lever is:

$$ b_R F_R = b_M F_M $$

The effort force is already known and has the value $ F_M = 200 \ \text{N} $.

$$ b_R F_R = b_M \cdot 200 \ (\text{N}) $$

The resisting force is given by the weight of the sack.

$$ F_R = mg = 200 \ (\text{kg}) \cdot 9.81 \ (\text{N/kg}) = 1962 \ \text{N} $$

Substituting $ F_R = 1962 \ \text{N} $ into the equilibrium condition, we obtain:

$$ b_R \cdot (1962 \ \text{N}) = b_M \cdot 200 \ (\text{N}) $$

$$ b_R \cdot 1962 = b_M \cdot 200 $$

Solving for $ b_R $ gives:

$$ b_R = \frac{b_M \cdot 200}{1962} $$

$$ b_R = b_M \cdot 0.102 $$

Since the total length of the lever is $ L = b_R + b_M = 3.00 \ \text{m} $, the effort arm can be expressed as $ b_M = 3.00 \ \text{m} - b_R $.

$$ b_R = (3.00 \ \text{m} - b_R) \cdot 0.102 $$

$$ b_R = 0.306 \ \text{m} - b_R \cdot 0.102 $$

$$ b_R + b_R \cdot 0.102 = 0.306 \ \text{m} $$

$$ b_R \cdot (1 + 0.102) = 0.306 \ \text{m} $$

$$ b_R \cdot 1.102 = 0.306 \ \text{m} $$

$$ b_R = \frac{0.306 \ \text{m}}{1.102} $$

$$ b_R \approx 0.28 \ \text{m} $$

Under equilibrium conditions, the fulcrum must therefore be located at a distance of $ 0.28 \ \text{m} $ from the sack.

For completeness, the length of the effort arm is:

$$ b_M = 3.00 - 0.28 = 2.72 \ \text{m} $$

The lever is thus mechanically advantageous, since the effort arm is significantly longer than the resisting arm ( $ b_M > b_R $ ).  

Exercise 3

A bottle opener with a total length of 10 cm is used to remove the crown cap from a bottle.

The distance between the fulcrum and the point of contact with the cap is 2 centimeters, and the cap exerts a resisting force of 100 N.

What driving force must be applied at the free end of the bottle opener?

For simplicity, we introduce an xy reference frame, choosing the x axis to coincide with the axis of the bottle opener.

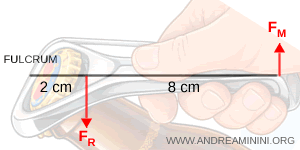
The lever is in equilibrium when the moments of the forces about the fulcrum are equal in magnitude:

$$ b_R F_R = b_M F_M $$

The given quantities are $ b_R = 2 \ cm = 0.02 \ m $, $ b_M = ( 10 - 2 ) \ cm = 0.08 \ m $, and $ F_R = 100 \ N $.

$$ ( 0.02 \ m ) \cdot ( 100 \ N ) = (0.08 \ m ) \cdot F_M $$

We simplify by canceling the unit of length $ m $ on both sides of the equation.

$$ 0.02 \cdot ( 100 \ N ) = 0.08  \cdot F_M $$

Solving the equation for the driving force yields

$$ F_M = \frac{ 0.02 \cdot ( 100 \ N ) }{0.08} = 25 \ N $$

Therefore, in order to open the bottle, a driving force of at least 25 N must be applied at the end of the opener.

In real conditions, the required force must be slightly greater than this theoretical value to account for friction, elastic deformations, and other mechanical losses.

And so on.