Center of Mass

The center of mass is the point at which the entire mass of an object, or of a system of objects, can be treated as if it were concentrated for the purpose of analyzing motion and force interactions.

Although it is an abstract construct, it plays a central role in mechanics because it allows us to replace an extended, complex body with a single representative point. This substitution preserves the essential physics while making the analysis far more tractable.

The center of mass behaves as though all external forces act on a single point carrying the full mass of the system. Its motion therefore captures the system’s overall translational behavior.

For example, in studying the dynamics of a rigid body, we can model its translational motion as that of a point particle located at its center of mass. This drastically simplifies many calculations.

Where is the center of mass located?

The position of the center of mass depends on how mass is distributed within the object. For many uniform or symmetric bodies, it coincides with the geometric centroid.

centroid example diagram

Consider a simple example: a rigid rod with two masses, $m_1$ and $m_2$, attached at its ends and suspended from a point P. The rod balances horizontally when the torques about P cancel.

$$ m_1 x_1 = m_2 x_2 $$

When this condition holds, the suspension point P lies at the system’s center of mass.

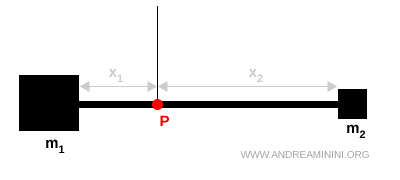
torque equilibrium diagram

Note. Here the rod’s own mass is ignored for simplicity. If the rod had non-negligible mass, its weight and corresponding lever arm would need to be included in the torque balance.

For a rigid body of irregular shape, the center of mass can be found experimentally by suspending the object from two different points and tracing the vertical lines through the suspension points.

As an example, imagine hanging a tennis racket from point $ P_1 $ and letting it settle into static equilibrium.

The center of mass must lie somewhere along the vertical through $ P_1 $, though its precise location is not yet known. We mark this vertical half line as $ r_1 $.

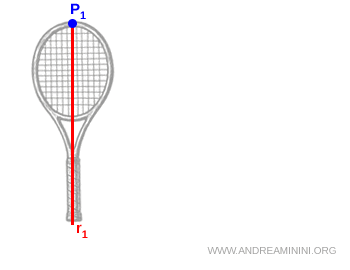
first suspension point diagram

Note. In equilibrium, the gravitational force acts along $ r_1 $, and the net torque on the racket is zero. This is why the racket does not rotate once it has come to rest.

Next, we suspend the racket from a second point $ P_2 $ and draw the corresponding vertical line $ r_2 $.

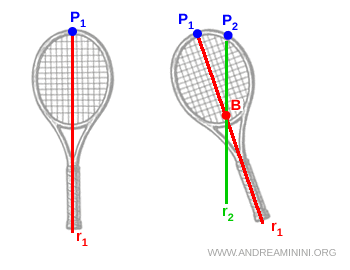
intersection locating the center of mass

The two lines $ r_1 $ and $ r_2 $ intersect at a single point $ B $.

That point is the center of mass of the racket.

A Practical Example

Consider a 10 kg crate resting on an inclined ramp.

crate on incline diagram

Several forces act on the crate, including gravity, the normal force from the surface, and friction.

To streamline the analysis, we identify the crate’s centroid $C$ and treat all forces as if they were applied at this single point.

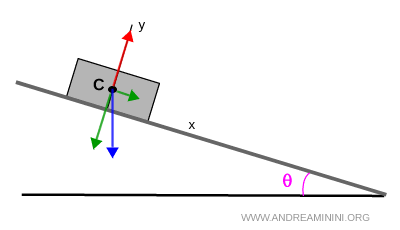
force decomposition at center of mass

This approach makes the vector decomposition of forces considerably easier.

Note. This simplification assumes that the crate’s mass is uniformly distributed. If the mass were not uniform, the actual center of mass would need to be computed by weighting each portion of the object according to its mass.

Example 2

A 2 kg mass is placed at 0 m, and a 3 kg mass is placed at 4 m along a horizontal rod.

two masses on a horizontal rod

We therefore have $m_1 = 2 \ kg$ at $x_1 = 0 \ m$ and $m_2 = 3 \ kg$ at $x_2 = 4 \ m$.

The center of mass is found using the standard expression.

$$ x_{cm} = \frac{ m_1 x_1 + m_2 x_2 }{ m_1 + m_2 } $$

$$ x_{cm} = \frac{2 \cdot 0 + 3 \cdot 4}{2 + 3} = \frac{12}{5} = 2.4 \, \text{m}
$$

This shows that the center of mass lies closer to the heavier mass, as physical intuition would suggest.

center of mass position diagram

Once the center of mass is known, the translational motion of the system can be modeled as that of a single point particle.

And so on.