Parity Operator

The parity operator is the mathematical operator that represents spatial reflection, namely the transformation that inverts the spatial coordinates of a system with respect to the origin.

In practical terms, applying parity means replacing a physical configuration with its mirror image, obtained by reversing the orientation of space.

For example, if a point in space has coordinates

$$ x = (x, y, z) $$

then the action of the parity operator $ P $ gives

$$ P(x) = (-x, -y, -z) $$

This transformation is known as a spatial inversion.

Applying the parity operator to a physical system is therefore equivalent to observing it in a mirror placed at the origin, rather than across a plane.

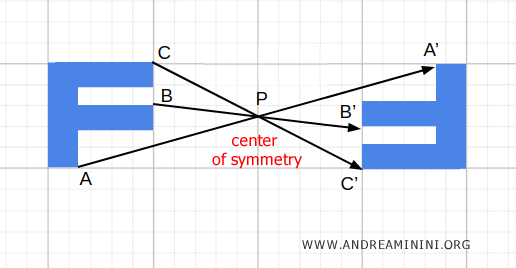
From a geometric perspective, this corresponds to a central symmetry. It is a global transformation that simultaneously reverses left and right, forward and backward, up and down.

What is it used for?

The parity operator plays a fundamental role in physics because parity is conserved in some fundamental interactions but violated in others.

• If a physical process remains unchanged under this transformation, parity is said to be conserved.
• If the process changes, parity is said to be violated.

The parity operator therefore provides a powerful criterion for classifying physical systems and particles.

Note. In electromagnetic and strong interactions, parity is conserved. In weak interactions, however, parity is violated. In this case, nature distinguishes between left and right. This is precisely why only left-handed neutrinos and right-handed antineutrinos exist. The violation of parity reveals one of the deepest asymmetries in nature.

Fundamental properties

The parity operator has several important properties.

If it is applied twice, the parity operator restores the system to its original configuration.

$$ P^2 = I $$

where $ I $ denotes the identity operator.

Example. Consider a point in space with coordinates: \[ \vec r = (2,-1,3) \] The parity operator inverts all coordinates: \[ P(\vec r) = (-2,1,-3) \] This corresponds to reflecting the point through the origin. Applying the parity operator once more gives: \[ P(P(\vec r)) = P(-2,1,-3) = (2,-1,3) \] We recover the original point, that is, \( P^2 = I \). \[ P^2(\vec r) = \vec r \]

From a physical standpoint, this means that performing a spatial inversion twice is equivalent to doing nothing. The system returns to its initial configuration.

For this reason, the parity operator $ P $ has only two possible eigenvalues: +1 and -1.

• +1 corresponds to an even-parity state
• -1 corresponds to an odd-parity state

Polar vectors and axial vectors

The parity operator also allows us to distinguish between polar vectors and axial vectors.

• Polar vectors
  A polar vector, such as position, velocity, or force, changes sign under spatial inversion: $$ P(\vec{v}) = -\vec{v} $$
• Axial vectors
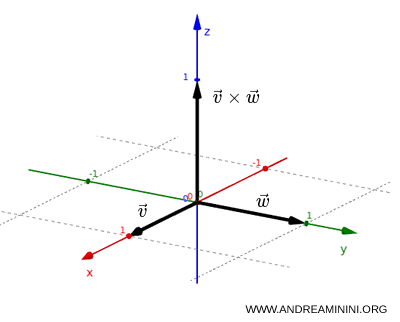
  An axial vector, also known as a pseudovector, such as angular momentum or the magnetic field, does not change sign under spatial inversion: $$ P(\vec v \times \vec w) = (-\vec v) \times (-\vec w) = \vec v \times \vec w = \vec L $$

  Proof. Let \( \vec L = \vec v \times \vec w \), where \( \vec v \) and \( \vec w \) are polar vectors. Under the action of the parity operator \( P \), one has $$ P(\vec v) = -\vec v, \quad P(\vec w) = -\vec w $$ and therefore $$ P(\vec L) = \vec L $$ Example. Consider two vectors in the plane: $$ \vec v = (1,0), \qquad \vec w = (0,1) $$ Their cross product is a vector perpendicular to the plane, along the z axis: $$ \vec v \times \vec w = (0,0,1) $$ This vector is an axial vector. Applying spatial inversion gives: $$ (x,y) \rightarrow (-x,-y) $$ and therefore: $$ P(\vec v) = (-1,0), \quad P(\vec w) = (0,-1) $$ Recomputing the cross product: $$ P(\vec v) \times P(\vec w) = (-1,0) \times (0,-1) = (0,0,1) $$ The result is unchanged: $$ P(\vec v \times \vec w) = \vec v \times \vec w $$ The direction of the vector is preserved. Physically, spatial inversion reverses directions but not the sense of rotation.
  

Scalars and pseudoscalars

The parity operator also makes it possible to distinguish between scalar and pseudoscalar quantities.

• Scalar
  A quantity is called a scalar if it does not change sign under spatial inversion.

  Example. The temperature at a point is \( T = 20^\circ \text{C} \). If we apply spatial inversion, the temperature remains unchanged: $$ P(T) = T $$ Temperature has no direction and does not depend on spatial orientation. It therefore retains the same value and sign in the mirror configuration. This makes it a scalar quantity.

• Pseudoscalar
  A quantity is called a pseudoscalar if it changes sign under spatial inversion.

  Example. Consider three vectors: \[ \vec a = (1,0,0) \\ \vec b = (0,1,0) \\ \vec c = (0,0,1) \] Compute the scalar triple product: \[ S = \vec a \cdot (\vec b \times \vec c) \] Since \( \vec b \times \vec c = (1,0,0) \), we obtain: \[ S = \vec a \cdot (\vec b \times \vec c) = 1 \] Now apply parity: \[ P(\vec a) = (-1,0,0), \quad P(\vec b) = (0,-1,0), \quad P(\vec c) = (0,0,-1) \] We then compute: \[ P(S) = P(\vec a) \cdot (P(\vec b) \times P(\vec c)) \] \[ P(S) = (-1,0,0) \cdot \big( (0,-1,0) \times (0,0,-1) \big) \] Since \( (0,-1,0) \times (0,0,-1) = (1,0,0) \), we find: \[ P(S) = (-1,0,0) \cdot (1,0,0) = -1 \] The final result changes sign. This is a clear example of a pseudoscalar quantity.

Parity eigenvalues of scalars, pseudoscalars, vectors, and pseudovectors

The parity operator \( P \) acts on physical quantities by assigning to each of them a well-defined eigenvalue, which can take only the values +1 or -1.

Scalars are invariant under spatial inversion and are therefore associated with the eigenvalue +1.  Pseudoscalars, by contrast, reverse sign under a parity transformation and consequently have eigenvalue -1.

Quantity	Parity transformation	Eigenvalue
Scalar	\( P(s)=s \)	\( +1 \)
Pseudoscalar	\( P(p)=-p \)	\( -1 \)
Vector (or polar vector)	\( P(\vec v)=-\vec v \)	\( -1 \)
Pseudovector (or axial vector)	\( P(\vec a)=\vec a \)	\( +1 \)

The same transformation law applies to ordinary vectors, also known as polar vectors, such as displacement or velocity. When a parity operation is performed, these quantities reverse their direction and are therefore associated with the eigenvalue -1.

By contrast, pseudovectors, or axial vectors, such as angular momentum, remain unchanged under spatial inversion and are thus characterized by the eigenvalue +1.

In summary, scalars and pseudovectors are invariant under spatial inversion, that is, under a parity transformation.

Parity in particles

Parity is a quantum number of particles, on the same footing as spin, electric charge, isospin, strangeness, and related quantities. 

It describes how the quantum state of a particle transforms under a spatial inversion.

There are fundamental distinctions among the main families of particles.

• For fermions (particles with half-integer spin), the parity of a particle is opposite to that of the corresponding antiparticle.
• For bosons (particles with integer spin), by contrast, a particle and its antiparticle share the same parity.

In composite particles, the total parity is obtained as the product of the parities of the individual constituents. Parity is therefore a multiplicative quantum number. This feature distinguishes it from quantum numbers such as electric charge or strangeness, which are additive.

Hadrons

Because the strong interaction conserves parity, hadrons (baryons and mesons) are eigenstates of the parity operator and can be classified according to the corresponding eigenvalue:

$$ p = \pm 1 $$

Baryons

By convention, quarks are assigned a positive intrinsic parity:

$$ p(\text{quark}) = +1 $$

As a consequence, a baryon composed of three quarks has parity:

$$ p = (+1)^3 = +1 $$

Thus, baryons in their ground state have positive parity.

Mesons

Mesons consist of a quark and an antiquark. Since the antiquark carries intrinsic parity opposite to that of the quark, the parity of a meson in its ground state is -1:

$$ p = (+1) \cdot (-1) = -1 $$

For mesons in excited states, there is an additional contribution from the orbital angular momentum l. In this case, the parity is given by:

$$ p = (-1)^{l+1} $$

Here $ l $ denotes the orbital angular momentum associated with the relative motion of the quark-antiquark pair.

Photon

The photon is a vector particle with spin 1 and is associated with the electromagnetic vector potential. Its intrinsic parity is -1:

$$ p = -1 $$

For the photon, intrinsic parity is not directly observable in the same sense as for massive particles. Instead, it is defined through the transformation properties of the electromagnetic field under spatial inversion.

And so on.