Xi Particles

The Xi particle (pronounced "ksee," from the Greek letter Ξ) is a baryon, that is, a particle composed of three quarks. It belongs to the family of strange particles because it contains two strange quarks (s).

It is also known as a cascade baryon, since in particle detectors it typically undergoes a sequence of successive decay processes rather than a single transition.

There are two main Xi particles:

• $ \Xi^0 $, composed of the quarks (u, s, s), that is, one up quark (u) and two strange quarks (s)
• $ \Xi^- $, composed of the quarks (d, s, s), that is, one down quark (d) and two strange quarks (s)

In both cases, the presence of two strange quarks is the defining feature that distinguishes Xi particles from protons and neutrons.

Electric charge

The two Xi particles carry the following electric charges:

• $ \Xi^0 $ has electric charge 0
• $ \Xi^- $ has electric charge -1

The total electric charge is obtained by summing the charges of the individual quarks.

• $ q(u) = +2/3 $
• $ q(d) = -1/3 $
• $ q(s) = -1/3 $

Spin and classification

Xi particles fall into two families, in close analogy with the Sigma baryons:

• Ordinary Xi (Ξ)
  These particles have spin \( \frac{1}{2} \) and belong to the baryon octet. In this configuration, the quark spins are not all aligned (for example ↑↑↓). As a result, the total spin is one half. $$ \tfrac 12 + \tfrac 12 - \tfrac 12 = \tfrac 12 $$
• Xi star (Ξ*)
  These particles have spin \( \frac{3}{2} \) and belong to the baryon decuplet. The quarks are in an excited configuration, with all spins aligned (↑↑↑). Consequently, the total spin is three halves. $$ \tfrac 12 + \tfrac 12 + \tfrac 12 = \frac{1+1+1}{2} = \tfrac 32 $$

The Xi particles occupy a well defined position within the Eightfold Way classification scheme.

They appear in the lower levels of the multiplet diagrams because they carry a strangeness of -2.

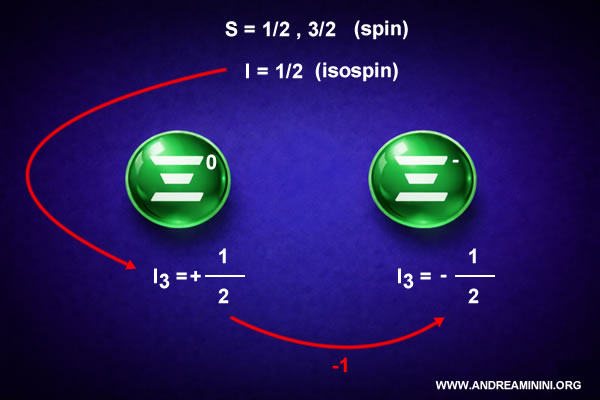
Isospin of the Xi particles

The Xi particles (Ξ) form an isospin doublet because they contain two strange quarks (s), while the remaining quark is either an up quark (u) or a down quark (d).

Since only up and down quarks contribute to isospin, and the strange quark has isospin zero, only one quark contributes an isospin of $ \frac 12 $.

This implies that the total isospin of the Xi particles is:

$$ I = \tfrac{1}{2} $$

The third component of isospin, $ I_3 $, can take two possible values:

• \( I_3 = +\tfrac{1}{2} \)
• \( I_3 = -\tfrac{1}{2} \)

As a result, only two distinct states exist:

• $ \Xi^0 $ (uss) with isospin $ I_3 = \tfrac12 $
• $ \Xi^- $ (dss) with isospin $ I_3 = -\tfrac12 $

This is why the Xi particles form a doublet, closely analogous to the proton - neutron system.

Note. As a quick consistency check, the number of quantum states associated with a particle multiplet is related to its isospin by the relation $$ 2I + 1 $$ In the case of the Xi particles, two distinct states are observed, so we must have $$ 2I + 1 = 2 $$ This immediately gives $$ I = \frac{2-1}{2} = \tfrac12 $$ This confirms that the Xi particles form an isospin doublet.

Decay

The Xi particles decay via the weak interaction, for example:

$$ \Xi^- \to \Lambda^0 + \pi^- $$

This decay is slow compared with strong interactions, precisely because it involves a change in strangeness.

And so on.