Eightfold Way
The Eightfold Way is a classification scheme for subatomic particles that groups baryons and mesons into families with shared properties, using two key quantum numbers:
- Electric charge $Q$
- Strangeness $S$, a quantum number indicating the presence of strange quarks or antiquarks within the particle.
It was introduced in 1961 by Murray Gell-Mann and, independently, by Yuval Ne’eman, based on the mathematical symmetry group SU(3).
The Eightfold Way aimed to bring order to the so-called “particle zoo” of the 1950s and ’60s - a time when dozens of new particles had been discovered, yet no coherent system existed to organize them.
These classifications are often depicted using regular geometric patterns such as hexagons and triangles.
Example
In the baryon scheme, strangeness $S$ is plotted on the vertical axis, while electric charge $Q$ appears along the diagonal axes.
This arrangement is known as the baryon octet.
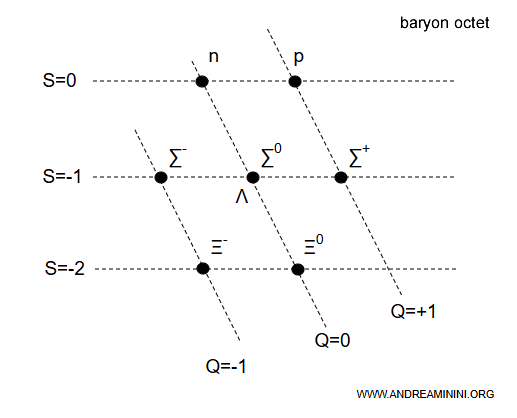
It’s called an “octet” because this hexagonal diagram contains eight baryons.
Note. In this diagram, baryons - spin $ \frac{1}{2} $ particles composed of three quarks - are arranged according to their strangeness ($S$, vertical axis) and electric charge ($Q$, horizontal axis).
- At the top, with $S = 0$, are the neutron $n$ (neutral, $Q = 0$) and the proton $p$ (positively charged, $Q = +1$).
- At $S = -1$ appear the three $\Sigma$ baryons ($\Sigma^{+}$, $\Sigma^{0}$, $\Sigma^{-}$) along with the $\Lambda$ baryon ($Q = 0$).
- At the bottom, with $S = -2$, are the $\Xi$ baryons, each containing two strange quarks $s$. The $ \Xi^{-} = (d s s) $ carries a negative charge ($Q = -1$), while the $ \Xi^{0} = (u s s) $ is neutral ($Q = 0$).
A similar hexagonal layout is used for mesons.
Here is the meson octet:
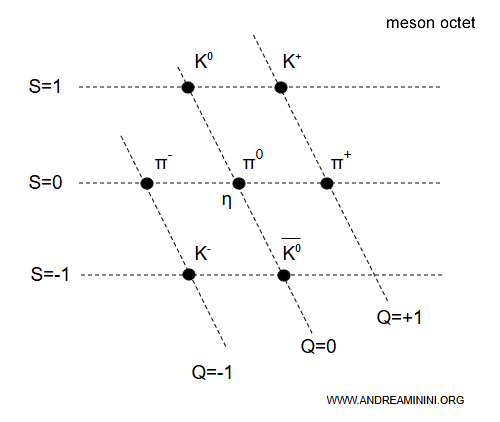
In this case, the top row corresponds to $S = +1$ and the bottom row to $S = -1$, the opposite of the baryon arrangement.
Note. This diagram shows pseudoscalar mesons - particles made of one quark and one antiquark - arranged by strangeness ($S$, vertical axis) and electric charge ($Q$, horizontal axis).
- At the top, with $S = +1$, are the neutral kaon $K^{0}$ ($Q = 0$) and the positively charged kaon $K^{+}$ ($Q = +1$).
- At $S = 0$ are the three pions ($\pi^{-}$, $\pi^{0}$, $\pi^{+}$) along with the $\eta$ meson.
- At the bottom, with $S = -1$, are the negatively charged kaon $K^{-}$ ($Q = -1$) and the neutral antikaon $\overline{K}^{0}$ ($Q = 0$). This arrangement reflects the $SU(3)$ flavor symmetry, grouping these mesons into an octet according to their quantum numbers.
These groupings were instrumental in providing the first systematic classification of strange particles, incorporating the newly defined “strangeness” quantum number introduced in the 1950s.
The scheme even led to the prediction of previously unknown particles - most famously, the $ \Omega^- $ (charge $-1$, strangeness $-3$), discovered in 1964.
That said, the model has its limitations.
Note. The symmetry is only approximate, and particle masses within the same multiplet are not identical. The model also doesn’t account for why particles have specific masses or interact in particular ways.
Nevertheless, it was a groundbreaking step toward particle classification and paved the way for the quark model, in which the octet and decuplet particles are understood as combinations of three quarks ($u$, $d$, $s$).
Baryon Decuplet
After the identification of the baryon octet with spin \( \tfrac12 \), physicists soon discovered the existence of additional particles with very similar properties but a higher intrinsic spin, namely \( \tfrac32 \).
These new states could not be accommodated within the known octet. However, their remarkably regular pattern made it clear that they were not accidental. Instead, they revealed a deeper and more structured realization of SU(3) symmetry than originally expected.
From a mathematical perspective, combining three quarks in the fundamental representation of SU(3) leads to the decomposition
$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$
Here, the representation $ 10 $ corresponds to the decuplet, $ 8 $ to the octet, and $ 1 $ to a singlet.
In other words, the existence of an octet naturally implies the existence of a decuplet, since both emerge from the same underlying SU(3) symmetry.
The baryon decuplet consists of states that are fully symmetric in flavor space. Because of this maximal symmetry, all particles in the decuplet have total spin \( \tfrac32 \).
Unlike the octet, which forms a hexagonal pattern with a central state, the decuplet is arranged as an equilateral triangle, consisting of ten states distributed across four distinct levels.
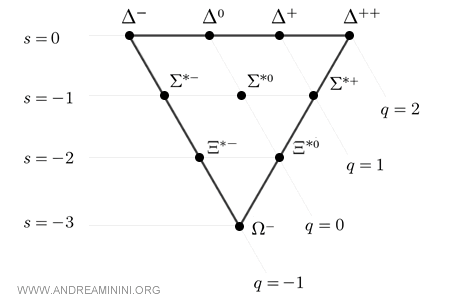
Note. The triangular geometry is not merely a visual choice. It reflects a deep physical property. In the decuplet, the quark spins are fully aligned, giving a total spin of \( \tfrac32 \), and the internal symmetry is therefore maximal.
The decuplet diagram is constructed using two quantum numbers: strangeness \( S \) and electric charge \( Q \). Moving downward in the diagram, the strangeness decreases while the number of strange quarks increases.
At the top of the triangle lie four \( \Delta \) particles, which contain no strange quarks and are composed exclusively of up \( u \) and down \( d \) quarks.
- \( \Delta^{++} = uuu \)
- \( \Delta^{+} = uud \)
- \( \Delta^{0} = udd \)
- \( \Delta^{-} = ddd \)
Just below them appear three \( \Sigma \) particles, each containing one strange quark \( s \) and two light quarks. The presence of the strange quark breaks the symmetry and increases the mass relative to the \( \Delta \) states.
- \( \Sigma^{*+} = uus \)
- \( \Sigma^{*0} = uds \)
- \( \Sigma^{*-} = dds \)
Note. The asterisk indicates a state with spin \( \tfrac32 \). The difference between \( \Sigma \) and \( \Sigma^{*} \) does not lie in their quark content, which is identical, but in how the quark spins combine. When all spins are aligned (↑↑↑), the total spin is \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] When the spins are not fully aligned (↑↑↓, ↑↓↑, ↓↑↑), the result is \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] and the state belongs to the octet. The same reasoning applies to the \( \Xi^{*} \) baryons.
At the next level appear two \( \Xi \) particles, each composed of two strange quarks and one light quark. Their masses are correspondingly higher.
- \( \Xi^{*0} = uss \)
- \( \Xi^{*-} = dss \)
At the base of the triangle lies a single particle, the \( \Omega^{-} \), composed entirely of strange quarks:
$$ \Omega^{-} = sss $$
This particle marks the lowest point of the decuplet and is characterized by strangeness \( S = -3 \), electric charge \( Q = -1 \), and spin \( \tfrac32 \).
The prediction of the \( \Omega^{-} \). One of the most striking successes of the quark model was the prediction of the \( \Omega^{-} \) particle. This state occupies the lowest vertex of the decuplet and completes the symmetric structure anticipated by theory. At the time the model was formulated, it had not yet been observed experimentally. Its discovery in 1964 provided compelling confirmation of SU(3) symmetry and the predictive power of the quark model.
And beyond.
