Quantum Theory

Quantum theory was first introduced in 1900 by the German physicist Max Planck to explain the distribution of electromagnetic radiation emitted by a blackbody - an ideal object that absorbs and re-emits all incoming radiation.

Planck proposed that energy is not released as a smooth, continuous flow, as had been assumed, but in discrete “packets” known as quanta. The energy of each quantum is proportional to the frequency of the radiation:

$$ E = h \cdot \nu $$

Where $h$ is Planck’s constant.

This idea is called quantization. Put simply, a physical system cannot take on arbitrary energy values but only integer multiples of a fundamental unit.

What does it mean to quantize? An analogy can help. Desert dunes appear to be continuous waves of sand, but they are in fact made up of countless individual grains - discrete units. In the same way, phenomena that seem continuous to us (such as radiation energy, electron motion, or atomic vibrations) turn out to be quantized at the microscopic scale.

A photograph works the same way: from a distance it looks smooth and continuous, but zoom in and it reveals a grid of bright dots - pixels.

Why did Planck introduce the quantum?

At the start of the 20th century, it was already known that the energy emitted by a heated body depends on its temperature.

To study this under ideal conditions, scientists defined the concept of a blackbody, an object that absorbs and re-emits all incident radiation, regardless of its composition.

Measurements showed that for any absolute temperature $T$, the emitted energy $E(\lambda)$ is spread across wavelengths $\lambda$ in a characteristic curve with a peak that shifts with temperature.

These curves take on a distinctive “bell shape.”

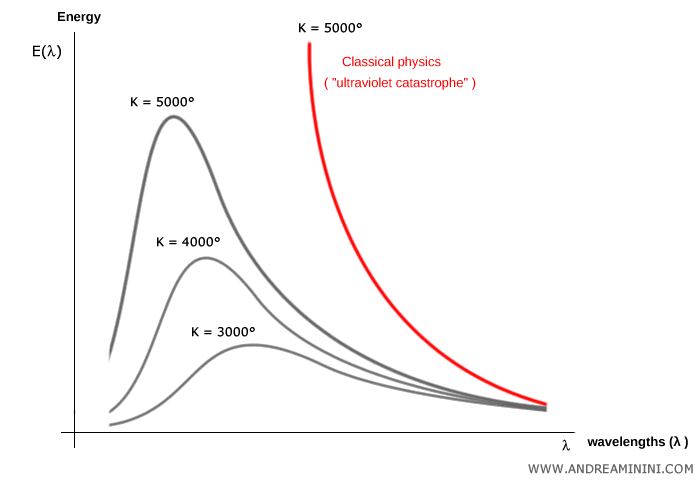
Classical physics, however, could not account for this behavior. Electromagnetic theory predicted that a blackbody should emit radiation continuously across all frequencies, with intensity rising without bound as frequency increased.

This led to the so-called ultraviolet catastrophe: the nonsensical prediction that a blackbody would radiate infinite energy at high frequencies.

Some classical laws still held. For example, the Stefan - Boltzmann law established that the total power emitted by a blackbody is proportional to the fourth power of its temperature:

$$ E = \sigma T^4 $$

Where $\sigma$ is the Stefan - Boltzmann constant.

The unresolved question was how energy is distributed across different wavelengths.

To answer it, Planck proposed a radical idea: electromagnetic energy is not continuous but comes in discrete packets - quanta. This is where Planck’s constant enters the picture.

What is Planck’s constant?

If energy is quantized, it cannot vary smoothly but only in integer multiples of a fundamental unit.

According to Planck, the energy of electromagnetic radiation of frequency $\nu$ is given by:

$$ E = h \nu $$

Where:

• $E$ is the energy of a quantum,
• $\nu$ is the frequency of the radiation,
• $h$ is Planck’s constant, approximately $6.626 \times 10^{-34} \, \mathrm{J \cdot s}$.

The constant $h$ is a universal constant that defines the minimum scale at which energy can be “packaged.” It is not itself a quantum, but the factor that links a quantum of energy to the radiation frequency.

From the simple formula to Planck’s law

With this insight, Planck derived the equation describing the spectral distribution of energy emitted by a blackbody:

$$ E(\nu) = \frac{8 \pi h \nu^3}{c^3} \cdot \frac{1}{e^{h\nu/kT}-1} $$

Here $c$ is the speed of light, $k$ is Boltzmann’s constant, and $T$ is the absolute temperature.

This law reproduces the bell-shaped emission curves and resolves the ultraviolet catastrophe of classical physics.

Planck’s law also bridges the two known limits: the Rayleigh - Jeans law (low frequencies) and Wien’s law (high frequencies).

In essence, Planck’s constant marks the boundary between classical and quantum physics: below this scale, phenomena are no longer continuous but quantized.

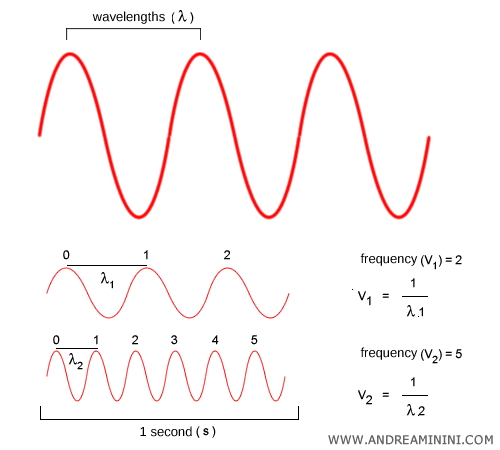
Frequency vs. wavelength. Frequency $\nu$ and wavelength $\lambda$ are two ways of describing the same wave: $$ c = \lambda \nu $$ Frequency ($\nu$) tells us how many oscillations occur per second. Wavelength ($\lambda$) is the distance between two successive crests. As frequency increases, wavelength decreases, and vice versa.

To appreciate this microscopic scale, consider an electron orbiting the nucleus of a hydrogen atom along a circular path (2πr).

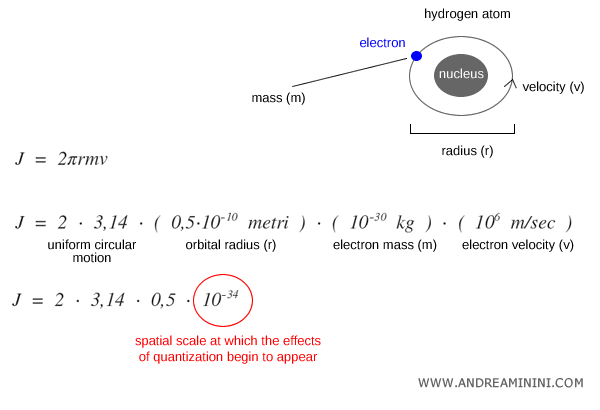
For an electron with mass $m \approx 9.1 \times 10^{-31}\,\text{kg}$, orbital radius $r \approx 0.5 \times 10^{-10}\,\text{m}$, and velocity $v \approx 10^6\,\text{m/s}$, the angular momentum is:

$$ J = 2 \pi r m v \sim 10^{-34} \, \text{J·s} $$

This value matches the order of magnitude of Planck’s constant $h$.

At this scale, classical mechanics fails, and the quantization of energy levels (Bohr’s model, quantum mechanics) becomes essential.

The difference between quanta and electromagnetic waves

In classical electromagnetic theory, light is treated as a continuous wave that distributes its energy smoothly across the frequency spectrum.

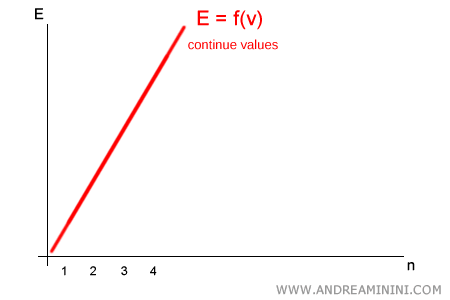
Planck, however, argued that energy is not continuous: it can only take on discrete values, integer multiples of the elementary quantum $h\nu$. In other words:

$$ E = n \cdot h\nu \qquad (n = 1,2,3,\dots) $$

No intermediate values exist between $1 \cdot h\nu$ and $2 \cdot h\nu$: a system can emit or absorb only whole numbers of quanta.

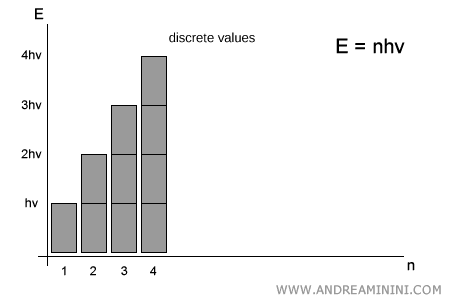
This view introduced a new picture of light: not just as a wave, but also as a stream of particles - photons - each carrying an energy $h\nu$.

The wave description was not abandoned, however: both wave and particle models remain valid and complementary.

Wave - particle duality

Subsequent developments in quantum mechanics showed that electromagnetic radiation has a dual character:

• in some experiments it behaves like a wave (interference, diffraction);
• in others it behaves like a particle (photoelectric effect, collisions with electrons).

This is known as wave - particle duality. Both aspects coexist and manifest depending on the experimental setup.

And the effect is not unique to light: electrons, protons, and neutrons also exhibit wave-like properties, as demonstrated by electron diffraction experiments.

The photoelectric effect

Planck’s quantum hypothesis, proposed in 1900 to explain blackbody radiation, quickly proved essential in other, unexpected contexts.

In 1905 Albert Einstein applied the quantum concept to the photoelectric effect, a phenomenon known since the late 19th century: when light strikes a metal surface, electrons are emitted from it.

Classical electromagnetism predicted that the energy carried by light should depend only on its intensity - that is, the wave’s amplitude.

By that logic, sufficiently intense light of any color ought to free electrons from a metal. Yet experiments revealed otherwise:

• If the light frequency ($\nu$) is too low (for example, red light), no electrons are emitted, no matter how intense the beam.
• If the frequency ($\nu$) exceeds a certain threshold (for instance, ultraviolet light), even a weak beam ejects electrons instantly.

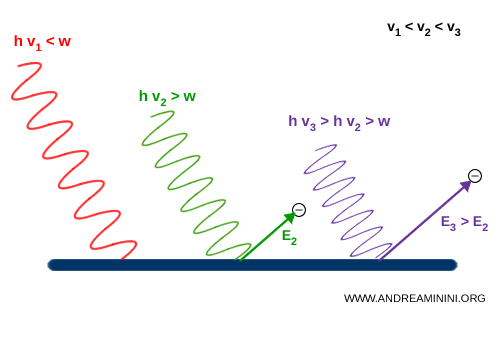
Einstein explained this by proposing that light consists of energy quanta - now called photons - each carrying a quantized amount of energy:

$$ E = h \nu $$

A photon striking a metal can transfer its energy to an electron.

If this energy exceeds the work function $W$ (the minimum required to free an electron from the metal), the electron is emitted. If not, nothing happens - regardless of the light’s intensity.

$$ E_{kin} = h \nu - W $$

This explanation confirmed the particle nature of electromagnetic radiation alongside its wave nature.

Note. For this work Einstein received the 1921 Nobel Prize in Physics, and the photoelectric effect became one of the decisive confirmations of quantum theory.

The Bohr atomic model

In 1913 Niels Bohr proposed a new atomic model to resolve contradictions left unresolved by classical physics.

Classical theory predicted that an electron orbiting the nucleus should radiate energy continuously, spiral inward, and collapse into the nucleus - making atoms unstable and impossible.

Bohr introduced a bold idea: electrons can occupy only specific stationary orbits corresponding to discrete energy levels. In these orbits, electrons do not radiate energy, and the atom remains stable.

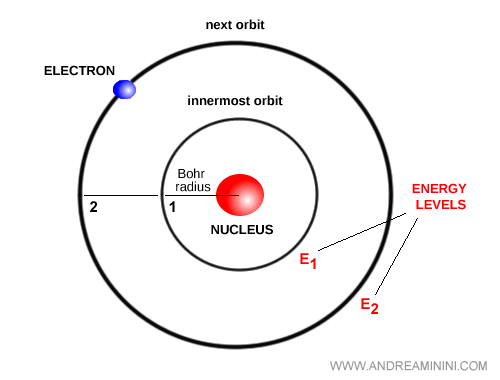
When an electron transitions between levels, the atom emits or absorbs a photon with energy equal to the difference between the two levels: $E = h \nu$.

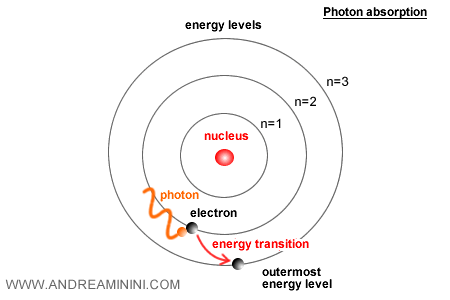
This allowed Bohr to explain the hydrogen emission spectrum with great precision, reproducing the sequence of its spectral lines.

Bohr’s contribution was decisive: it incorporated the concept of the quantum of energy (introduced by Planck and Einstein) into the atomic structure itself, marking a fundamental step toward quantum mechanics.

From Quantum Theory to Quantum Mechanics

In the years that followed, the quantum hypothesis was broadened to cover other phenomena: de Broglie’s matter waves (1924), Schrödinger’s wave mechanics, and Heisenberg’s matrix mechanics (1925 - 26).

• De Broglie’s Matter-Wave Hypothesis (1924)
  Louis de Broglie proposed that not only light, but also material particles (such as electrons and protons), could display wave-like properties. Each particle with momentum $p$ would have an associated wavelength: $$ \lambda = \frac{h}{p} $$  This bold idea extended wave - particle duality from light to matter itself.
• Heisenberg’s Matrix Mechanics (1925)
  Drawing on experimental data from atomic spectra, Werner Heisenberg developed a mathematical framework built on matrices rather than trajectories or visualized waves. In this approach, physical quantities are represented by operators that obey specific commutation rules, giving rise to the uncertainty principle. Shortly thereafter, Born and Jordan formalized the matrix method with Heisenberg (the Born - Jordan - Heisenberg paper). Though abstract, this formulation proved equivalent to Schrödinger’s and helped establish the foundations of modern quantum mechanics.
• Schrödinger’s Wave Mechanics (1926)
  Erwin Schrödinger introduced an equation that describes the time evolution of the wavefunction $\psi$, which encodes all the information about a system’s quantum state. In this picture, the electron is no longer a tiny particle orbiting the nucleus but a probability wave spread through space. The stationary solutions of Schrödinger’s equation account for the discrete energy levels of atoms. His first paper on wave mechanics appeared in early 1926, and it was soon shown to be mathematically equivalent to Heisenberg’s matrix mechanics.
• Born’s Probabilistic Interpretation (1926)
  Max Born proposed that the square of the wavefunction, $|\psi|^2$, should be interpreted as a probability density. This interpretation gave wave mechanics physical meaning; without it, the theory would have remained elegant mathematics with little connection to reality.
• Heisenberg’s Uncertainty Principle (1927)
  Heisenberg formulated the uncertainty principle ($\Delta x \cdot \Delta p \geq \hbar/2$), which clarified the conceptual implications of the new mechanics.
• Dirac and Unification (1926 - 1928)
  Paul Dirac played a crucial role in showing the formal equivalence of Heisenberg’s matrix mechanics and Schrödinger’s wave mechanics. In 1928 he introduced his famous relativistic equation of the electron, which unified quantum mechanics with special relativity and naturally predicted the existence of the electron’s antiparticle: the positron, discovered experimentally by Carl Anderson in 1932.
• The Solvay Conference (1927)
  Held in Brussels in October 1927 under the theme “Electrons and Photons,” it focused on the foundations of the newly emerging quantum mechanics. Nearly all the great physicists of the era attended: Planck, Einstein, Bohr, Heisenberg, Schrödinger, Dirac, Born, Pauli, de Broglie, Lorentz, and many others. The famous group photograph shows 29 participants, 17 of whom either were or would become Nobel laureates. The Solvay Conference marked the decisive triumph of quantum mechanics: the ideas of Bohr, Heisenberg, Schrödinger, and Born became the new framework of physics. At the same time, Dirac was finalizing his relativistic electron theory (1928), completing the picture. From this point forward, classical physics remained valid only as a macroscopic approximation, while quantum physics became the fundamental description of the microscopic world.

  The Einstein - Bohr Debate. Einstein rejected Born’s probabilistic interpretation, defended vigorously by Bohr and Heisenberg. His famous line was: “God does not play dice with the universe.” Bohr retorted that it was not the role of physics to tell God what to do, defending the Copenhagen interpretation. This debate over the nature of quantum reality would continue for decades.

• Toward Quantum Field Theory (1930s - 1940s)
  After the development of “non-relativistic” quantum mechanics, physicists pushed toward a relativistic field theory. This gave rise first to relativistic quantum mechanics and then to quantum electrodynamics (QED). QED treats electromagnetic radiation as a quantized field and describes interactions among electrons, positrons, and photons with remarkable precision. It paved the way for quantum theories of the other fundamental forces, including quantum chromodynamics (QCD) and the Standard Model, and remains one of the most successful examples of quantum field theory.

Out of this convergence of ideas, quantum mechanics emerged - a new framework that, from the 1920s onward, revolutionized our understanding of the microscopic world.

The transition from quantum theory to quantum mechanics was not the achievement of a single mind, but the result of a collective effort in which many scientists played decisive roles.

And the story continued.