Angular momentum of particles
In quantum mechanics, the angular momentum of a particle describes how its quantum state transforms under spatial rotations, meaning how the wavefunction carries and exhibits rotational properties.
There are two distinct types of angular momentum:
- Orbital angular momentum \( L \)
This quantity is associated with the angular structure of the wavefunction in space. It does not depict a particle orbiting like a planet, but rather the symmetry of its probability distribution. The quantization of \( L \) reflects the rotational properties of a system in ordinary three dimensional space. - Intrinsic angular momentum (spin) \( S \)
Spin is an internal property of a particle and does not correspond to a physical rotation in real space. It is a purely quantum mechanical form of angular momentum, described mathematically by SU(2) transformations, with no true analogue in classical physics.
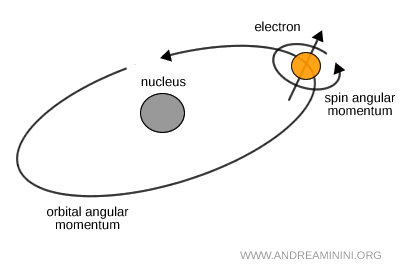
Note. A common misconception is to imagine spin as a literal rotation of the particle around its own axis. In reality, spin is not a mechanical motion in space, but an intrinsic quantum property. There is no tiny rotating object and no exact classical picture. Spin produces measurable effects, such as magnetic moments and energy level splitting, but it does not correspond to any spatial geometry or orbital structure in three dimensions, unlike orbital angular momentum \( L \). This distinction is crucial.
Orbital Angular momentum in quantum physics
In classical mechanics, once the angular momentum vector \( \vec{L} = \vec{r} \times m\vec{v} \) is known, it can always be decomposed into its three Cartesian components \( L_x \), \( L_y \) and \( L_z \).
$$ \vec{L} = (L_x,\,L_y,\,L_z) $$
These components, \( L_x, L_y, L_z \), are simply the projections of \( \vec{L} \) along the Cartesian axes \( x, y, z \).
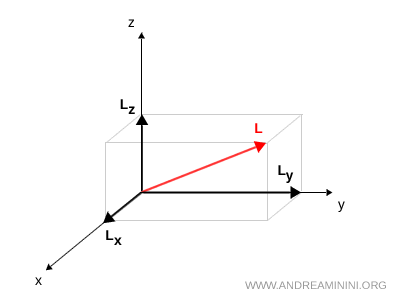
In quantum mechanics this decomposition cannot be carried out simultaneously, because measuring one component, for instance \( L_x \), inevitably alters the measurable values of the other two, \( L_y \) and \( L_z \). This prevents all three components from being determined with exact precision at the same time.
Therefore, it is impossible to measure all components of a particle’s angular momentum simultaneously.
Experimentally, only one projection can be measured at a time. By convention, measurements are performed along the \( z \) axis, so the measurable component is \( L_z \).
In addition to \( L_z \), one can measure the magnitude of the angular momentum vector \( \vec{L} \), given by
$$ L = \sqrt{l(l+1)}\,\hbar $$
Here \( l \) is a non negative integer quantum number, \( l = 0,1,2,3,\dots \), and \( \hbar \) is the reduced Planck constant, the quantity that sets the scale of quantum phenomena and defines the “granularity” of the microscopic world.
Note. The constant \( \hbar \), pronounced h-bar, is fundamental in quantum mechanics: $$ \hbar = \frac{h}{2\pi} $$ where \( h \) is Planck’s constant and \( \hbar \) is the reduced Planck constant. In other words, \( \hbar \) is simply \( h \) divided by \( 2\pi \). Its value is approximately $$ \hbar \approx 1.054 \times 10^{-34} , \text{J·s} $$ It appears so frequently because it simplifies quantum formulas and makes equations more compact, which is why it is present in all fundamental relations of quantum theory.
From the expression \( L = \sqrt{l(l+1)}\,\hbar \) it follows that the magnitude of angular momentum can only take discrete values.
This means that the magnitude \( |\vec{L}| \) does not vary continuously, but instead changes in discrete steps determined by the quantum number \( l \).
| \(l\) | \(|\vec{L}|=\sqrt{l(l+1)}\,\hbar\) | Value |
|---|---|---|
| 0 | \(\sqrt{0\cdot 1}\,\hbar\) | \(0\) |
| 1 | \(\sqrt{1\cdot 2}\,\hbar\) | \(\sqrt{2}\,\hbar\) |
| 2 | \(\sqrt{2\cdot 3}\,\hbar\) | \(\sqrt{6}\,\hbar\) |
| 3 | \(\sqrt{3\cdot 4}\,\hbar\) | \(\sqrt{12}\,\hbar\) |
| 4 | \(\sqrt{4\cdot 5}\,\hbar\) | \(\sqrt{20}\,\hbar\) |
| 5 | \(\sqrt{5\cdot 6}\,\hbar\) | \(\sqrt{30}\,\hbar\) |
In many cases it is more practical to use the squared magnitude \( L^2 \), which simplifies calculations.
$$ L^2 = l(l+1)\hbar^2 $$
This avoids the square root in \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar \) and makes algebraic manipulation easier, especially in problems involving operators or the addition of angular momenta.
| \(l\) | \(L^2 = l(l+1)\hbar^2\) | Value |
|---|---|---|
| 0 | \(0\cdot 1\,\hbar^2\) | \(0\,\hbar^2\) |
| 1 | \(1\cdot 2\,\hbar^2\) | \(2\,\hbar^2\) |
| 2 | \(2\cdot 3\,\hbar^2\) | \(6\,\hbar^2\) |
| 3 | \(3\cdot 4\,\hbar^2\) | \(12\,\hbar^2\) |
| 4 | \(4\cdot 5\,\hbar^2\) | \(20\,\hbar^2\) |
| 5 | \(5\cdot 6\,\hbar^2\) | \(30\,\hbar^2\) |
In quantum mechanics it is the operator \( \hat{L}^2 \) that possesses well defined eigenvalues, which is why it is often more natural to work with \( L^2 \) rather than with the magnitude \( |\vec{L}| \).
Note. This quantization has no analogue in classical physics, where the magnitude of angular momentum can take any real value.
The projection of the orbital angular momentum onto the \( z \) axis is also quantized and is given by
$$ L_z = m_l \hbar $$
Here \( m_l \) is the magnetic quantum number. It can only take integer values ranging from \( -l \) to \( l \):
$$ m_l = -l, -l+1, \dots, -1, 0, +1, \dots, l-1, l $$
The table below summarizes the allowed values of \( m_l \) and the corresponding values of \( L_z \).
| \(l\) | Allowed values of \(m_l\) | Corresponding values of \(L_z\) | Number of states \((2l+1)\) |
|---|---|---|---|
| 0 | \(0\) | \(0\) | 1 |
| 1 | \(-1,\,0,\,+1\) | \(-\hbar,\,0,\,+\hbar\) | 3 |
| 2 | \(-2,\,-1,\,0,\,+1,\,+2\) | \(-2\hbar,\,-\hbar,\,0,\,+\hbar,\,+2\hbar\) | 5 |
| 3 | \(-3,\,-2,\,-1,\,0,\,+1,\,+2,\,+3\) | \(-3\hbar,\,-2\hbar,\,-\hbar,\,0,\,+\hbar,\,+2\hbar,\,+3\hbar\) | 7 |
For instance, if \( l = 2 \) then the projection of \( \vec{L} \) along the \( z \) axis can only take five values: \(-2\hbar, -\hbar, 0, +\hbar, +2\hbar\).
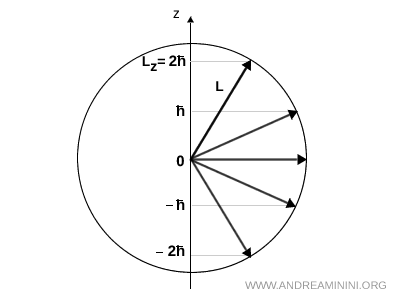
In this illustration the magnitude of the angular momentum is fixed by \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar \), so all vectors have the same length and lie on the surface of a sphere.
The \( z \) projection, on the other hand, can only take the discrete values \( L_z = m_l \hbar \) with \( m_l = -2, -1, 0, +1, +2 \).
The five arrows represent the allowed vectors \( \vec{L} \) for \( l = 2 \).
Each vector has the same magnitude \( |\vec{L}| \), but forms a different angle with the \( z \) axis, in order to satisfy the condition \( L_z = m_l \hbar \).
Note. From this example we see that even when \( m_l \) is at its maximum value \( (m_l = l) \), the vector can never lie exactly along the \( z \) axis. If it did, we would have \( |\vec{L}| = |L_z| \), but in reality \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar > l\hbar = L_z^{\text{max}} \). Therefore the vector must always retain non zero components along the other axes, which gives rise to its spatial precession.
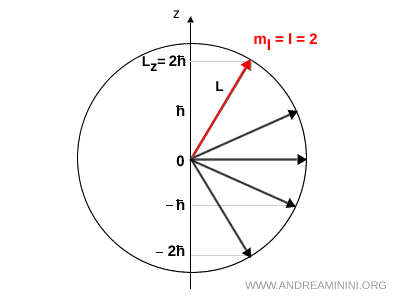
It is also worth emphasizing that \( L_z \) is a signed projection of the angular momentum along the \( z \) axis. It can therefore be positive, negative or zero.
For this reason, \( L_z \) must not be interpreted as a magnitude, but as a vector component in a specific direction. A magnitude is always positive, while a vector component can change sign.
Spin Angular Momentum
Spin is the intrinsic angular momentum of a particle.
Unlike orbital angular momentum, it is not associated with motion through space. Spin is a fundamental quantum property, on the same level as mass and electric charge.
It is characterized by two compatible quantities, closely mirroring the orbital case.
The magnitude of the intrinsic angular momentum vector is
$$ S = \sqrt{ s(s+1) } \hbar $$
In many calculations, it is more convenient to work with the squared magnitude:
$$ S^2 = s(s+1) \hbar^2 $$
Here \( s \) is the spin quantum number, which can take integer or half-integer values:
$$ s = 0, \tfrac12, 1, \tfrac32, 2, \tfrac52, \ldots $$
The projection of the spin vector \( \vec{S} \) along the z axis is quantized and given by
$$ S_z = m_s \hbar $$
where \( m_s \) is the spin magnetic quantum number. It can take the discrete values \( m_s = -s, -s+1, \ldots, s-1, s \), yielding a total of \( 2s+1 \) possible spin states.
For instance, if \( s = \tfrac{1}{2} \), then \( m_s = +\tfrac{1}{2} \) corresponds to the spin up state and \( m_s = -\tfrac{1}{2} \) corresponds to the spin down state.
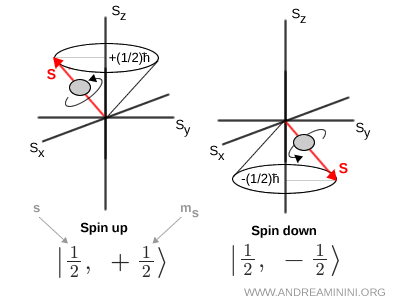
It is also common to use bra-ket notation to represent spin states, writing \( | s,\ m_s \rangle \). In this language, \( \left| \tfrac12,\ +\tfrac12 \right\rangle \) denotes spin up and \( \left| \tfrac12,\ -\tfrac12 \right\rangle \) denotes spin down.
Note. Orbital angular momentum is associated with spatial motion, whereas spin is intrinsic. Despite this difference, both quantities have a quantized magnitude and a single measurable component along a chosen axis.
The table below shows some representative values of \( s \) and \( m_s \).
| \( s \) | \( S^2 = s(s+1)\hbar^2 \) | Possible values of \( m_s \) | Corresponding values of \( S_z \) | States \( 2s+1 \) |
|---|---|---|---|---|
| \( \tfrac12 \) | \( \tfrac34 \hbar^2 \) | \( -\tfrac12, +\tfrac12 \) | \( -\tfrac12\hbar, +\tfrac12\hbar \) | 2 |
| \( 1 \) | \( 2\hbar^2 \) | \( -1, 0, +1 \) | \( -\hbar, 0, +\hbar \) | 3 |
| \( \tfrac32 \) | \( \tfrac{15}{4}\hbar^2 \) | \( -\tfrac32, -\tfrac12, +\tfrac12, +\tfrac32 \) | \( -\tfrac32\hbar, -\tfrac12\hbar, +\tfrac12\hbar, +\tfrac32\hbar \) | 4 |
Mathematically, spin obeys the same angular momentum algebra as orbital motion. Physically, however, it is not the rotation of a tiny sphere. It is an intrinsic quantum degree of freedom, revealed through the quantized values of \( S^2 \) and \( S_z \).
While a particle may occupy states with different orbital angular momentum \( l \), its spin \( s \) is an immutable property of the particle itself and cannot be altered.
For example, every proton, neutron and electron has spin \( s = \tfrac{1}{2} \). Photons and gluons, on the other hand, have spin \( s = 1 \).
| Bosons (integer spin) | Fermions (half-integer spin) | ||
|---|---|---|---|
| Spin 0 | Spin 1 | Spin \( \tfrac{1}{2} \) | Spin \( \tfrac{3}{2} \) |
| Pseudoscalar mesons $ \pi, K, \eta, \eta' $ |
Photons ( \( \gamma \) ) Gluons ( \( g \) ) Bosons \( W^+, W^-, Z \) Vector mesons $ \rho, \omega, \phi, K^*, J/\psi, \Upsilon $ |
Quarks, leptons protons ( \( p \) ), neutrons ( \( n \) ) electrons ( \( e \) ) Baryon octet $ p,\ n , \Sigma^{+},\ \Sigma^{0},\ \Sigma^{-} $ $ \Xi^{0},\ \Xi^{-} , \Lambda^{0} $ |
Baryon decuplet $ \Delta^{++},\ \Delta^{+},\ \Delta^{0},\ \Delta^{-} $ $ \Sigma^{*+},\ \Sigma^{*0},\ \Sigma^{*-} $ $ \Xi^{*0},\ \Xi^{*-} $ $ \Omega^{-} $ |
Particles with integer spin are known as bosons, and they follow Bose-Einstein statistics.
Particles with half-integer spin are known as fermions, and they obey the Pauli exclusion principle.
Note. A distinctive feature of fermions is that their spin eigenstates return to their original configuration only after a \( 4\pi \) rotation. This striking property reflects the half-integer nature of \( s \) and \( m_s \).
A practical example
Consider an electron in a (p) orbital, characterized by the orbital quantum number
$$ l = 1 $$
For an electron in a (p) orbital there are two types of angular momentum:
- \( L \) describes the spatial symmetry of the wavefunction and determines the shape and rotational structure of the orbital
- \( S \) is an internal degree of freedom that determines the spin state and is independent of the orbital geometry
Let us now examine these two angular momenta separately.
1) Orbital angular momentum \( \mathbf{L} \)
For \( l = 1 \) we have
$$ L^2 = l(l+1)\hbar^2 = 2\hbar^2 $$
$$ |\mathbf{L}| = \sqrt{2}\,\hbar $$
where \( \hbar \) is the reduced Planck constant.
This means that the wavefunction has a well defined rotational structure. The (p) orbitals, often depicted with their familiar "two lobes", correspond to the spherical harmonics
$$ Y_1^{-1},\; Y_1^{0},\; Y_1^{+1} $$
associated with the three possible values
$$ m_l = -1,\; 0,\; +1 $$
Physically, \( \mathbf{L} \) does not point along a fixed direction. Instead it precesses, tracing out a cone.
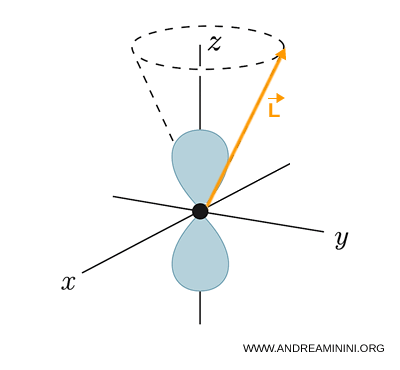
The asymmetric angular shape of (p) orbitals arises precisely because \( l = 1 \).
In this sense, the shape of the orbital is the visible manifestation of orbital angular momentum.
2) Spin angular momentum \( \mathbf{S} \)
The electron also possesses spin:
$$ s = \frac{1}{2} $$
with the allowed values
$$ m_s = \pm \frac{1}{2} $$
Thus, for each (p) orbital the electron can occupy two possible spin states:
- (p) with spin up \( (m_s = +\tfrac{1}{2}) \)
- (p) with spin down \( (m_s = -\tfrac{1}{2}) \)
Spin is not the result of any real rotation in space. There is no physical spinning motion of the electron about its own axis.
Spin does not alter the spatial form of the orbital, because it is not tied to geometry. It is an intrinsic internal property of the particle.
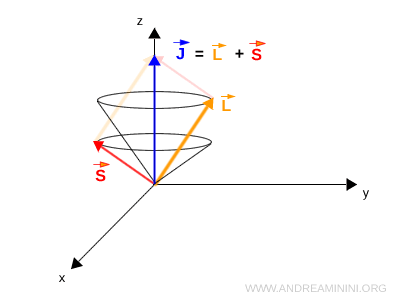
In summary, a single quantum state contains two contributions to angular momentum: the orbital contribution \( L \) and the spin contribution \( S \).
Their vector sum defines the total angular momentum \( J \):
$$ \mathbf{J} = \mathbf{L} + \mathbf{S} $$
This coupling produces small energy splittings between the possible states, which are observed in atomic spectra as the fine structure.
What are the cones in the diagram? The vectors are not stationary. They undergo precession, meaning they rotate around an axis much like a spinning top that is slightly tilted. Specifically, \( L \) and \( S \) precess around \( J \). In turn, \( J \) precesses around the direction of the magnetic field, which is the vertical axis in the image. This motion creates the cone shaped surfaces. In the presence of an external magnetic field the atom senses the field and the total angular momentum \( J \) is forced to precess around its direction. This is why \( J \) distributes itself around the vertical \( z \) axis.
Adding quantum angular momenta
In classical physics, adding two angular momenta is routine. You simply add vectors component by component and the result is completely fixed.
Quantum mechanics works under very different constraints. Because the components of the angular momentum operator do not commute, you cannot know all three simultaneously.
This is where the real challenge emerges. How do you combine two angular momenta when their individual components cannot be specified at the same time?
For a quantum system, only two quantities are sharply defined for an angular momentum:
- its z component, given by the eigenvalue \( m \) of \( J_z \)
- its total angular momentum, given by the quantum number \( j \) associated with \( J^2 \)
Since the notion of a definite spatial orientation for the angular momentum vector has no physical meaning in quantum mechanics, classical vector addition simply does not apply.
One rule, however, remains intact: the z components add directly:
$$ m = m_1 + m_2 $$
The difficulty lies in determining the total angular momentum because its magnitude is not predetermined.
The reason is that the relative orientation of the two angular momenta is not a well defined observable. They may behave as if they were more or less aligned, but that alignment cannot be fixed or measured in the classical sense.
Consequently, the total angular momentum does not collapse to a single value. Instead it can take a discrete set of allowed quantum numbers spanning a minimum and a maximum:
$$ j = \lvert j_1 - j_2 \rvert,\ \lvert j_1 - j_2 \rvert + 1,\ \ldots,\ ( j_1 + j_2 ) - 1 ,\ (j_1 + j_2) $$
If the angular momenta were effectively parallel, the total would be \( j_1 + j_2 \). If they were effectively antiparallel, it would be \( |j_1 - j_2| \).
All intermediate configurations correspond to quantized, equally spaced values in this interval.
$$ j = \lvert j_1 - j_2 \rvert, \underbrace{ \ \lvert j_1 - j_2 \rvert + 1,\ \ldots,\ ( j_1 + j_2 ) - 1 }_{quantized \ value } ,\ (j_1 + j_2) $$
This discreteness reflects the quantization of the eigenvalues of \( J^2 \). The total angular momentum can only take integer or half integer values such as \( j = 0, \frac{1}{2}, 1, \frac{3}{2}, 2, ... \). Arbitrary values are excluded by the operator algebra.
Example. Consider a particle with spin 1 in an orbital state with angular momentum \( l = 3 \). We need to combine:
- the orbital angular momentum \( j_1 = 3 \)
- the spin angular momentum \( j_2 = 1 \)
If the two angular momenta acted as if they were parallel, the total would be \( j_1 + j_2 = 4 \). If they acted as if they were antiparallel, it would be \( |j_1 - j_2| = 2 \). The allowed values therefore run from 2 to 4. Since only discrete values are possible, the total angular momentum can take the three values: $$ j = 2, 3, 4 $$ In short, the particle can combine its orbital and spin angular momenta in three distinct ways, each associated with a different energy level and therefore with a different physical state.
When two quantum angular momenta are added, the outcome is never a single number. Instead we obtain a discrete spectrum of possible totals.
The z components add in the usual way, but the total angular momentum can only occupy specific quantized values between a lower and an upper bound.
And so on.
