Spin in Quantum Mechanics

Spin is a fundamental quantum number carried by every elementary particle. Along with quantities such as energy and orbital angular momentum, it helps determine the complete quantum state of a physical system.

Spin is not the result of any literal motion through space. It is an intrinsic degree of freedom that belongs to the particle itself.

Although it behaves mathematically like a form of angular momentum and has the same physical dimensions (kg⋅m²/s), spin does not correspond to the mechanical rotation of an object in space.

Example. The electron is modeled as a structureless point particle with no spatial extent. It therefore has no physical axis to rotate around, so it cannot be imagined as a tiny spinning sphere.

Spin takes only quantized values, which occur in integer or half integer multiples of $\hbar$, the reduced Planck constant.

$$ s = 0,\ \tfrac{1}{2},\ 1,\ \tfrac{3}{2},\ 2,\ \tfrac{5}{2},\ \dots $$

Particles are classified according to their spin:

Bosons have integer spin (0, 1, 2, …) and include particles such as photons and gluons.
Fermions have half integer spin ($\frac{1}{2}$, $\frac{3}{2}$, …) and include electrons, protons and neutrinos.

Spin $ \tfrac{1}{2} $ is especially significant because it characterizes the particles that make up atoms and bulk matter: protons, neutrons and electrons.

An electron with spin $\tfrac{1}{2}$ can occupy only two eigenstates along any chosen direction:

"up": $+\tfrac{1}{2}$
"down": $-\tfrac{1}{2}$

Half integer spin cannot be represented by an ordinary three dimensional vector. It requires a spinor.

example

Spinors are two component objects that transform under the appropriate unitary representation of the rotation group.

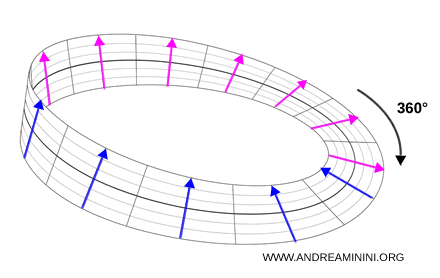
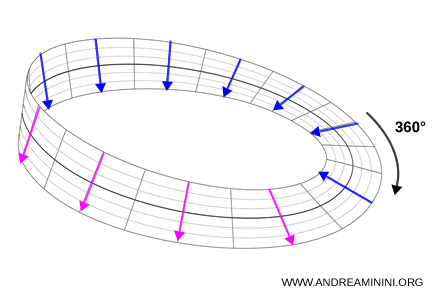
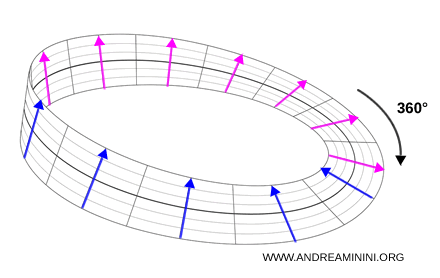
A remarkable feature of spinors is that a 360° rotation does not restore the original state. It produces the same spinor with the opposite sign. Only a 720° rotation brings the system back to its initial configuration. No classical system behaves this way.

This feature can be visualized using a Möbius strip. After a 360° turn, the arrow points in the opposite direction.

Möbius strip analogy illustrating spinor reversal after 360 degrees

A second full turn restores the original state.

spinor restored after 720 degree rotation

In the Pauli formalism, the spin of a spin 1/2 particle is represented by a two component spinor

$$ \chi = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$

The complex amplitudes $\alpha$ and $\beta$ encode the probabilities of measuring the particle in the spin up or spin down state.

Note. When the coordinate system is rotated, the spinor transforms according to a unitary operator: $$ \begin{pmatrix} \alpha' \\ \beta' \end{pmatrix} = U(\theta) \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$ where $ U(\theta) $ is a $ 2 \times 2 $ matrix of the form $$ U(\theta) = e^{- i \theta \cdot \sigma /2} $$ The vector $ \theta $ specifies the axis and angle of rotation following the right hand rule.

Spin 1 and Spin 1/2 Representations

The mathematical representation of a particle depends strongly on its spin.

Spin 1 particles (vector bosons such as photons) are represented by three component vectors in physical space. Their rotational behavior is described by the spin 1 representation of $ SO(3) $, the group of spatial rotations.
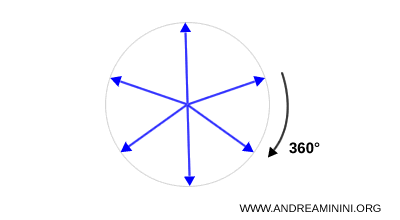
Spin $ \tfrac{1}{2} $ particles are described by two component spinors. Their rotation properties belong to $ SU(2) $, the double cover of $ SO(3) $. Because of this double cover structure, a 720° rotation is needed to return a spinor to its original state.

Note. The contrast between the $ 3 \times 3 $ representations of $ SO(3) $ and the $ 2 \times 2 $ representations of $ SU(2) $ captures the essential divide between classical integer spin and quantum half integer spin.
Spin $ \tfrac{3}{2} $ particles require four component spinors that transform under the four dimensional representation of $ SU(2) $. Their transformation properties display the same intrinsically quantum features seen in all half integer spins.

To summarize:

Spin 0 corresponds to a scalar representation (dimension 1)
Spin $ \tfrac{1}{2} $ corresponds to a spinor representation (dimension 2)
Spin 1 corresponds to a vector representation (dimension 3)
Spin $ \tfrac{3}{2} $ corresponds to a higher dimensional spinor representation (dimension 4)

Spin in Quantum Field Theory

Spin was first introduced in non relativistic quantum mechanics to explain observations such as fine structure in atomic spectra and the Zeeman effect.

In relativistic quantum mechanics, spin arises naturally from the Dirac equation, which describes the dynamics of the electron. The equation predicts spin $\tfrac{1}{2}$ states and accounts for key experimental results, including the electron's anomalous magnetic moment.

The Dirac formalism underpins several fundamental phenomena:

Pauli exclusion principle, which forbids two identical fermions from occupying the same quantum state.
Quantum statistics: bosons obey Bose Einstein statistics, while fermions follow Fermi Dirac statistics.
Magnetic properties: spin contributes to the magnetic dipole moments of fundamental particles.

Spin is thus one of the clearest examples of a genuinely quantum property with no classical analogue.

It was originally proposed to explain experimental anomalies, but it finds its full theoretical foundation only in the relativistic framework.

Spinors capture its structure, and through them we gain access to the quantum behavior, interactions and statistical properties of matter.

And so on.