Sigma Particles

Sigma particles, denoted by the Greek letter $ \Sigma $, are baryons composed of three quarks and belong to the family of particles that interact through the strong interaction. Their defining characteristic is the presence of a strange quark (s), which gives rise to the quantum number known as strangeness.

The Σ particles are composed of three quarks:

• $ \Sigma^+ = uus $
• $ \Sigma^0 = uds $
• $ \Sigma^- = dds $

In all cases, one of the quarks is a strange quark (s), while the remaining two are combinations of up (u) and down (d) quarks.

Electric charge

The electric charge of each particle is obtained by summing the electric charges of its constituent quarks, using the values:

• $ q(u) = +2/3 $
• $ q(d) = -1/3 $
• $ q(s) = -1/3 $

The resulting electric charges of the Sigma particles are therefore:

• $ q ( \Sigma^+ ) = +1 $
• $ q ( \Sigma^0 ) = 0 $
• $ q ( \Sigma^- ) = -1 $

For example, the particle $ \Sigma^+ $ is composed of two up quarks and one strange quark (uus). Its electric charge is therefore: $$ q ( \Sigma^+ ) = q(u) + q(u) + q(s) = \frac{2}{3} + \frac{2}{3} - \frac{1}{3} = \frac{2+2-1}{3} = \frac{3}{3} = +1 $$ The particle $ \Sigma^0 $ consists of one up quark, one down quark, and one strange quark (uds). Its electric charge is: $$ q ( \Sigma^0 ) = q(u) + q(d) + q(s) = \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = \frac{2-1-1}{3} = \frac{0}{3} = 0 $$ The particle $ \Sigma^- $ consists of two down quarks and one strange quark (dds). Its electric charge is: $$ q ( \Sigma^- ) = q(d) + q(d) + q(s) = - \frac{1}{3} - \frac{1}{3} - \frac{1}{3} = \frac{-1-1-1}{3} = -1 $$ 

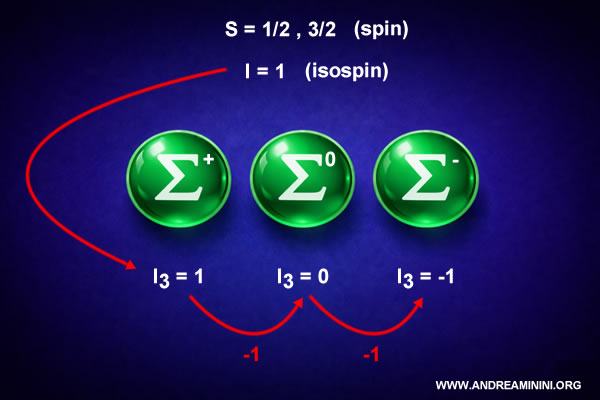
Isospin of the Sigma particles

The Sigma particles have a total isospin equal to 1.

This follows from the fact that isospin is carried only by the up and down quarks, while the strange quark does not contribute to isospin.

The two quarks u and d combine to form a symmetric state, yielding a total isospin:

$$ I = 1 $$

Explanation. The quarks $ u $ and $ d $ form an isospin doublet, whereas the strange quark does not participate in isospin and is therefore excluded from this part of the construction. Both the up and down quarks have isospin \( \tfrac12 \), with third components: $$ I_3(u) = +\frac{1}{2} $$ $$ I_3(d) = -\frac{1}{2} $$ The structure of the SU(2) group implies that combining two isospin-\( \tfrac12 \) states yields only two possible total isospin values, according to the same rules used for angular momentum addition: \[ \frac{1}{2} \otimes \frac{1}{2} = [ \frac{1}{2} + \frac{1}{2} ] \oplus [ \frac{1}{2} - \frac{1}{2} ] = 1 \oplus 0 \] This results in one symmetric state with \( I = 1 \) and one antisymmetric state with \( I = 0 \). The symmetric state with $ I = 1 $ forms a triplet corresponding to the Sigma particles: \[ \begin{aligned} |1,+1\rangle &= uu \\ |1,0\rangle &= \frac{1}{\sqrt2}(ud + du) \\ |1,-1\rangle &= dd \end{aligned} \] The antisymmetric state with \( I = 0 \) instead corresponds to the Lambda particle: \[ |0,0\rangle = \frac{1}{\sqrt2}(ud - du) \] At this point, it is important to note that the Sigma and Lambda particles share the same quark content (uds), yet they differ in their isospin structure.

Why is I = 1 assigned to the Sigma particles (Σ) and I = 0 to the Lambda (Λ)?

Experimentally, the Sigma particles are observed in three distinct charge states ($ Σ^+, Σ^0, Σ^- $). Since the number of states in an isospin multiplet is given by $ 2I + 1 $, it follows that the Sigma particles must have I = 1. $$ 2I + 1 = \color{red} 3 \to I = 1 $$ They therefore form a triplet. This implies that the isospin component of their wavefunction is symmetric, meaning it remains unchanged under the exchange of the u and d quarks. $$ uu $$ $$ dd $$ $$ \frac{1}{\sqrt{2}}(ud + du) $$ By contrast, the Lambda particle has I = 0 because it is observed experimentally in only a single state ( $ Λ^0 $ ). $$ 2I + 1 = \color{red} 1 \to I = 0 $$ Therefore, the Lambda is a singlet. In this case, the isospin wavefunction is antisymmetric, meaning that exchanging the u and d quarks changes the sign of the wavefunction. $$ \frac{1}{\sqrt{2}}(ud - du) $$ Thus, the difference between the Sigma and Lambda particles does not lie in their quark content, but in how the quarks are arranged in isospin space. 

If the total isospin is \( I = 1 \), then the number of possible states is:

\[ 2I + 1 = 2 \cdot 1 + 1 = 3 \]

This means that the isospin multiplet contains three distinct states, characterized by the values of the third component \( I_3 \):

$$ I_3 = \{ +1,\ 0,\ -1 \} $$

In the case of the Sigma particles, these three states correspond to:

• $ \Sigma^+ $
• $ \Sigma^0 $
• $ \Sigma^- $

Spin of the Sigma particles

There are two distinct families of Sigma particles, distinguished by the value of their total spin.

• Sigma (Σ)
  The ordinary Sigma particles have spin \( \frac{1}{2} \) and belong to the baryon octet. In this case, the quark spins are not all aligned (for example, one possible configuration is ↑↑↓), resulting in a total spin of 1/2. The sum of the spins is: $$ \tfrac 12 + \tfrac 12 - \tfrac 12 = \tfrac 12 $$
• Sigma star (Σ*)
  The Sigma* particles have spin \( \frac{3}{2} \) and belong to the baryon decuplet. In this case, all three quark spins are aligned (↑↑↑), yielding a total spin of 3/2. The sum is: $$ \tfrac 12 + \tfrac 12 + \tfrac 12 = \tfrac 32 $$ These states are excited baryons. The Sigma* particles therefore have fully aligned quark spins.

The difference between the two families arises from the alignment of the quark spins.

This explains why particles with identical quark content can nevertheless have different masses and different spin values.

And so on.