Photons
The photon is the elementary particle that represents the quantum of the electromagnetic field.
In quantum field theory, it is the carrier of the electromagnetic force, just as the gluon carries the strong force and the $ W $ and $ Z $ bosons carry the weak force.
The photon has zero rest mass and no electric charge. With spin 1, it is classified as a vector boson.
It always travels at the speed of light in a vacuum, $ c = 299{,}792{,}458 \ m/s $, and photons with the same energy are indistinguishable from one another.
Wave-particle duality
Photons display a dual nature:
- Wave-like, in phenomena such as interference, diffraction, and polarization.
- Particle-like, in phenomena such as the photoelectric effect, Compton scattering, and blackbody radiation.
This duality lies at the heart of quantum mechanics and underpins the principle of complementarity: a photon is not “wave or particle” but both, depending on how it is observed.
Energy and momentum
A photon’s energy is directly proportional to its frequency $\nu$, according to:
$$ E = h \nu $$
Here $h$ is Planck’s constant, $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $, and $\nu$ is the radiation frequency.
Although it has no rest mass, the photon carries momentum given by:
$$ p = \frac{E}{c} = \frac{h\nu}{c} = \frac{h}{\lambda} $$
where $\lambda$ is the wavelength.
The emergence of the photon concept
The photon was not discovered in a single experiment. Instead, the idea took shape gradually between 1900 and 1924.
Planck and quantized radiation (1900)
While investigating blackbody radiation, Max Planck proposed that electromagnetic radiation is emitted in discrete packets of energy, which he called quanta:
$$ E = h\nu $$
where $E$ is the energy of the electromagnetic radiation, $\nu$ its frequency, and $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $ is Planck’s constant.
In other words, a photon’s energy is proportional to its frequency $\nu$ and can take only discrete values - multiples of $h\nu$:
$$ E = n \cdot h\nu $$
with $ n = 1, 2, 3, \dots $ an integer counting the number of quanta.
For Planck, however, this quantization was not yet a fundamental feature of the electromagnetic field. He introduced it as a mathematical assumption to match theory with experiment and to resolve the so-called ultraviolet catastrophe.
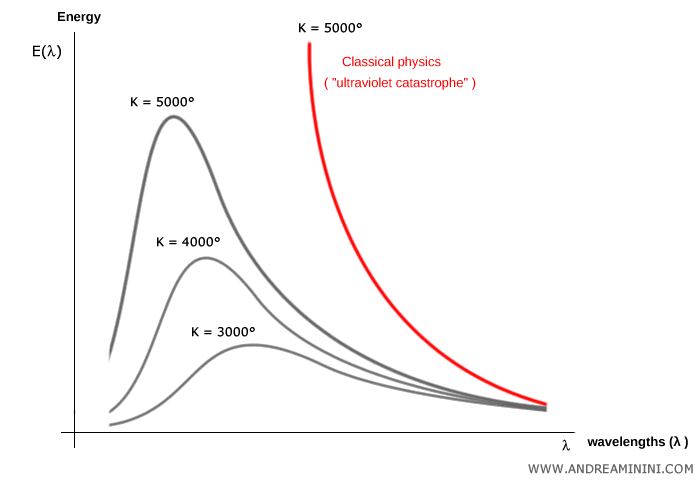
What was the ultraviolet catastrophe? The ultraviolet catastrophe was a paradox of classical physics at the end of the 19th century. It arose in attempts to explain the radiation emitted by a blackbody - an idealized object that absorbs and re-emits all incident electromagnetic radiation. Classical theory, based on electromagnetism and statistical mechanics (specifically the Rayleigh-Jeans law), predicted that the energy radiated per frequency $\nu$ should increase indefinitely with frequency:
$$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} kT $$
- $\rho(\nu, T)$ is the spectral energy density (energy per unit volume per frequency)
- $\nu$ is the radiation frequency
- $T$ is the body’s temperature
- $k$ is Boltzmann’s constant
- $c$ is the speed of light
This formula worked at low frequencies, but at high frequencies - in the ultraviolet and beyond - it predicted that the energy density would diverge to infinity. In other words, classical theory suggested that a blackbody should emit infinite energy at high frequencies. Experiments, however, showed a peak followed by a decline. Clearly, no physical object radiates infinite energy. This breakdown became known as the “ultraviolet catastrophe.”
Planck’s solution (1900)
Planck resolved the problem with a radical proposal: electromagnetic radiation is not continuous, but comes in discrete quanta:
$$ E = h \nu $$
where $E$ is the radiation energy, $\nu$ its frequency, and $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $, a constant chosen to fit experimental data. Energy exchange, he argued, could only occur in integer multiples of a basic unit:
$$ E = n h \nu \quad \text{with} \quad n = 1, 2, 3, \dots $$
Here $n$ is a positive integer. This fundamental unit $h\nu$ is the quantum of energy. Radiation could not be emitted or absorbed smoothly, but only in discrete “jumps,” indivisible packets of energy. This quantum is the basic unit of energy for radiation of a given frequency. Planck used this idea to derive a new formula for the spectral energy density - now known as Planck’s law:
$$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} \cdot \frac{h\nu}{e^{h\nu/(kT)} - 1} $$
Here $h\nu$ is the quantized photon energy. The formula reduces to the classical law at low frequencies ($h\nu \ll kT$) but falls off exponentially at high frequencies ($h\nu \gg kT$), avoiding the ultraviolet catastrophe. This was the first clear appearance of quantization in physics and marked the birth of quantum theory. It is worth noting that Planck himself did not claim to explain why radiation was quantized - he regarded it as a mathematical device to reconcile theory and experiment.
Einstein and the Photoelectric Effect (1905)
Einstein began with a familiar experimental observation: when a metal is exposed to ultraviolet light, or to light of sufficiently high frequency, electrons are ejected from its surface.
This phenomenon is known as the photoelectric effect.
The emitted electrons travel freely into space, as if the light had struck them and torn them away from the metal.
Note. Up to that point, light was understood as an electromagnetic wave that delivered energy continuously. By that logic, increasing the light’s intensity should have transferred more energy to the electrons. But experiments showed otherwise:
- Below a certain threshold frequency (light that was too “red”), no electrons were emitted, regardless of intensity.
- At higher frequencies (toward “blue” or “violet”), electrons were emitted with greater energy, even when the light was weak.
In 1905 Einstein offered a radical interpretation: light is not only a wave, but is made of discrete energy quanta - what we now call “photons.” Each photon carries an energy given by:
$$ E = h \nu $$
where $h$ is Planck’s constant and $\nu$ is the frequency of the light.
When a photon collides with an electron in the metal, it transfers all of its energy ($h\nu$). The electron uses part of this energy to overcome the binding energy, called the “work function” ($w$), and the rest appears as the electron’s kinetic energy:
$$ E_{\text{kinetic}} \leq h\nu - w $$
Einstein explained that if the frequency is too low, no electrons can be ejected, regardless of how intense the light is:
$$ w > h\nu $$
But once the frequency $\nu$ exceeds the threshold set by the work function, electrons are released:
$$ w \leq h\nu $$
The higher the frequency, the greater the kinetic energy of the emitted electrons. Increasing the light’s intensity only increases the number of electrons emitted, not their individual energies.
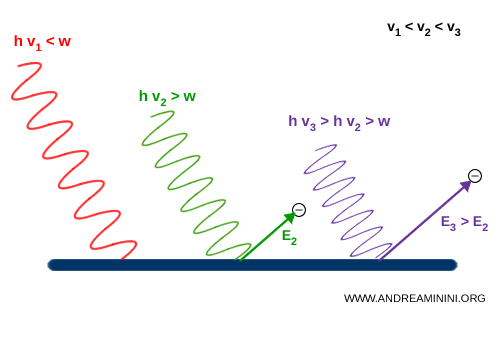
For instance: with radiation of frequency $ \nu_1 $ (red), the frequency is too low and no electrons are ejected. With radiation of frequency $ \nu_2 $ (green), the frequency is just sufficient, and electrons are emitted with kinetic energy $ E_2 $. With radiation of frequency $ \nu_3 $ (violet), the frequency is higher still, and the electrons emerge with greater energy $ E_3 > E_2 $.
Einstein thus realized that the energy of photoemitted electrons depends on the frequency of light, not on its intensity.
This simple yet revolutionary idea reshaped physics forever.
Note. Einstein’s proposal was controversial, as it recalled Newton’s old - and long discredited - corpuscular theory of light. Even Millikan, who experimentally confirmed Einstein’s formula, resisted its conceptual implications. Only after nearly two decades, with repeated experimental confirmations, did the scientific community fully accept the photon concept.
Compton’s experiment (1923)
In 1923 Arthur Compton provided decisive confirmation of light’s particle nature by measuring the shift in wavelength of scattered X-rays:
$$ \lambda' = \lambda + \lambda_c(1 - \cos\theta) $$
where $ \lambda_c $ is the Compton wavelength.
This relativistic elastic collision offered definitive proof that photons carry both energy and momentum.
Note. The term “photon” itself was introduced later, by Gilbert Lewis in 1926.
The Photon in Quantum Field Theory (QFT)
Quantum field theory replaced the classical picture of a continuous field with a quantized one. In this framework, the electromagnetic field consists of discrete quanta: photons.
Forces are no longer described as continuous influences spreading through space, but as exchanges of mediator particles between charges.
In the case of electromagnetism, these mediators are photons, acting as quantum messengers that can generate either attraction or repulsion, depending on the situation.
For example, the repulsion between two electrons can be reinterpreted as the continual exchange of virtual photons that transmit the interaction.
In summary, the photon began as Planck’s mathematical hypothesis, was reimagined by Einstein, and gained full experimental validation with Compton.
Its dual wave-particle character is properly understood only in the framework of quantum field theory, where it is the quantum of the electromagnetic field and the mediator of electromagnetic interactions.
The Photon in Quantum Physics
In classical physics, two charges (such as two electrons) repel because each generates an electric field that acts on the other.
In quantum physics, by contrast, the picture is one of a constant exchange of photons, as if the charges were perpetually trading “force carriers” that communicate attraction or repulsion.
Caution. It is misleading to imagine these mediators, like photons, as if they were tangible objects bouncing back and forth. Virtual photons can account for both attraction and repulsion, and their role is subtler than any simple mechanical analogy.
In atoms, for example, electrons remain bound to the nucleus because they are attracted by the positively charged protons. In quantum terms, this attraction is explained as the continuous exchange of virtual photons between electrons and protons.
Likewise, two electrons repel each other because of their identical charge - again described as the exchange of virtual photons.
This framework extends to all the fundamental forces:
- Electromagnetic force: two electrons repel by exchanging virtual photons, the mediators of the electromagnetic interaction.
- Weak force: in beta decay, a neutron transforms into a proton by emitting a $W^-$ boson, which then decays into an electron and an antineutrino.
- Strong force: quarks inside protons and neutrons remain bound through the exchange of gluons, which act as the “glue” of the nucleus.
- Gravity: in theory, masses attract by exchanging gravitons, hypothetical particles that have not yet been observed.
Note. In many contexts, classical physics still provides an excellent approximation - for example, Coulomb’s law for the electromagnetic field. This is because in stable systems like atoms, the exchange of an enormous number of virtual photons makes the field appear effectively continuous, and quantization effects become negligible. But in phenomena such as the photoelectric effect or Compton scattering, the quantum nature of light is unmistakable. Here, the field’s discrete structure cannot be ignored, and photons must be treated as genuine particles - quanta of energy beyond the reach of any continuous-field model.
And so on.
