SU(3) symmetry and the baryon Eightfold Way

Because many baryons display closely related physical properties, they are naturally described by a symmetry larger than isospin alone. This symmetry is SU(3), within which eight spin \( \tfrac12 \) baryons are grouped into an octet. This organizational scheme is known as the Eightfold Way.

The notion of symmetry arises because the laws governing the strong interaction remain invariant under transformations that exchange baryons sharing the same quantum numbers, apart from their position within the multiplet.

Put differently, the strong interaction does not differentiate among these baryons. They can be transformed into one another without affecting the underlying physics of the system.

This invariance is captured mathematically by the SU(3) group, which arranges the eight spin \( \tfrac12 \) baryons into a single irreducible representation known as the "Eightfold Way".

Note. The Eightfold Way was introduced in 1961 by the American theoretical physicist Murray Gell-Mann through a systematic classification of hadrons into multiplets organized according to SU(3) symmetry. At the time, this framework was purely phenomenological, grounded in experimentally observed regularities and lacking a microscopic interpretation. Only later, with the introduction of the quark model in 1964, also proposed by Gell-Mann, did this classification acquire a firm physical basis rooted in the internal structure of hadrons.

Origin of the symmetry

During the 1950s, physicists discovered an unexpectedly large variety of baryons.

Closer inspection revealed that eight of these baryons shared strikingly similar properties:

• proton \( p \)
• neutron \( n \)
• \( \Lambda \)
• \( \Sigma^+ , \Sigma^0 , \Sigma^- \)
• \( \Xi^0 , \Xi^- \)

All eight particles have spin \( \tfrac12 \), participate in the strong interaction, and possess masses of the same order of magnitude, ranging approximately from 940 to 1320 MeV/(c²).

This pattern strongly suggests that these particles are not independent entities, but rather members of a single baryon family.

A similar situation had already arisen in the 1930s for the proton and neutron, which were shown to be related by an SU(2) symmetry. The newly discovered pattern was conceptually analogous, but involved a larger set of particles.

Note. The proton and neutron have nearly identical masses and differ primarily in their electric charge. Werner Heisenberg proposed that they should be regarded as two states of a single particle, the nucleon. To formalize this idea, the concept of isospin was introduced and associated with the SU(2) symmetry group.

As additional baryons were discovered, physicists naturally asked whether a symmetry group larger than SU(2) might exist, one capable of accommodating all eight baryons simultaneously. This question became known as the eight-baryon problem.

Gell-Mann addressed this issue by proposing that SU(2) isospin is not a fundamental symmetry, but rather a subgroup of a more comprehensive symmetry.

That larger symmetry is the SU(3) group, within which baryons are not grouped arbitrarily, but arranged according to a precise and highly constrained symmetry structure.

Note. SU(3) is an abstract Lie group, analogous to SU(2), but characterized by eight generators rather than three. Among its irreducible representations is an eight-dimensional one, commonly referred to as the octet representation.

The eight baryons $ p, n, \Lambda, \Sigma^+, \Sigma^0, \Sigma^-, \Xi^0, \Xi^- $ form exactly an SU(3) octet.

This classification scheme is known as the Eightfold Way.

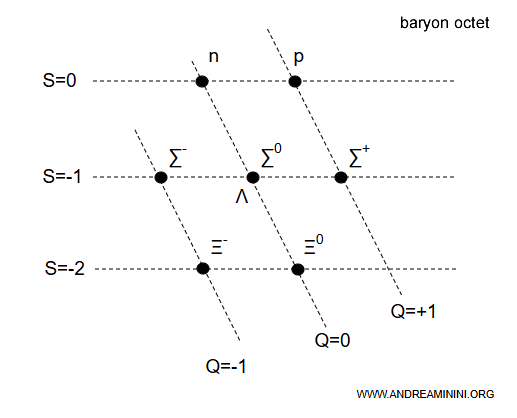
Within this framework, the eight particles are interpreted as distinct states of a single symmetry representation. This viewpoint not only clarifies the systematic relationships among the baryons, but also enables the prediction of previously unobserved states.

A notable example is the Ω⁻ particle, whose existence was inferred from the SU(3) scheme and later confirmed experimentally.

In much the same way that \( p \) and \( n \) constitute the two states of an SU(2) isospin doublet, the eight baryons correspond to states of an SU(3) representation.

The Eightfold Way and the quark model

The Eightfold Way is fundamentally a classification scheme rather than a microscopic model of hadronic structure.

By the late 1950s, it had become clear that many hadrons exhibited similar properties and could be organized into multiplets obeying symmetries such as SU(2) for isospin and SU(3) for flavor.

At that stage, however, these regularities were purely empirical. Neither their physical origin nor the internal structure of the particles involved was yet understood.

The situation changed with the introduction of the quark model by Murray Gell-Mann and, independently, by George Zweig. This development established that hadrons are not elementary particles, but composite systems built from more fundamental constituents known as quarks.

In the original formulation of the model, three light quarks were introduced: up (u), down (d), and strange (s).

quark	charge	isospin	strangeness
u	\( +\tfrac23 \)	\( +\tfrac12 \)	0
d	\( -\tfrac13 \)	\( -\tfrac12 \)	0
s	\( -\tfrac13 \)	0	-1

These three quarks \( (u, d, s) \) form the fundamental triplet representation of SU(3). This identification is the central structural element of the model.

SU(3) flavor symmetry relates the \( u \), \( d \), and \( s \) quarks, treating them as equivalent with respect to the strong interaction, aside from differences in their masses. Starting from these fundamental constituents, the observed spectrum and properties of hadrons can be understood in a unified and systematic way.

In particular, baryons are composed of three quarks.

$$ qqq $$

The combination of three SU(3) triplet representations yields:

$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$

This decomposition accounts for the observed baryon spectrum:

• 10 corresponds to the baryon decuplet with spin \( \tfrac32 \)
• 8 corresponds to the baryon octet with spin \( \tfrac12 \)
• 1 corresponds to a singlet state

Consequently, the existence of the baryon decuplet and octet is not an arbitrary assumption, but a direct mathematical consequence of SU(3) flavor symmetry.

As a concrete example, the baryon octet expressed in terms of quark content consists of eight baryons built from the quarks \( (u, d, s) \):

Baryon	composition
p	uud
n	udd
\( \Lambda \)	uds
\( \Sigma^+ \)	uus
\( \Sigma^0 \)	uds
\( \Sigma^- \)	dds
\( \Xi^0 \)	uss
\( \Xi^- \)	dss

This pattern is not accidental. SU(3) flavor symmetry is effective precisely because baryons are composed of three quarks drawn from the set \( (u, d, s) \).

From this perspective, the quark model provides the microscopic foundation of the Eightfold Way by introducing the quarks \( (u, d, s) \), which furnish the fundamental triplet representation of SU(3).

By combining these three quarks, the baryon multiplets that had originally been identified empirically within the Eightfold Way emerge naturally.

Note. SU(3) flavor symmetry is not exact, because the quark masses are not equal: $$ m_u \approx m_d \ll m_s $$ Consequently, SU(3) is only an approximate symmetry. The presence of strangeness breaks the symmetry, but the overall multiplet structure remains clearly recognizable. By contrast, SU(2) isospin symmetry is generally much more accurate.

The baryon decuplet

After the identification of the baryon octet with spin \( \tfrac12 \), experimental evidence revealed the existence of additional baryons with closely related properties but a different total spin, namely spin \( \tfrac32 \).

These states could not be accommodated within the known octet, yet their remarkably regular pattern made it clear that they were not accidental.

This strongly indicated that SU(3) symmetry is richer than originally anticipated.

An analysis of the configurations allowed by the mathematical structure of SU(3) shows that, in addition to the octet (8), other irreducible representations naturally arise, including a decuplet (10) and a singlet (1):

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

This decomposition is not a physical assumption but a direct and rigorous consequence of representation theory.

Note. In other words, if the octet exists, then the decuplet must also exist, since both emerge inevitably from the same underlying mathematical structure.

The baryon decuplet corresponds to states that are completely symmetric in flavor space and therefore to baryons with total spin \( \tfrac32 \).

Unlike the octet, which forms a hexagonal pattern with a central state, the decuplet takes the shape of an equilateral triangle consisting of ten states arranged across four distinct levels.

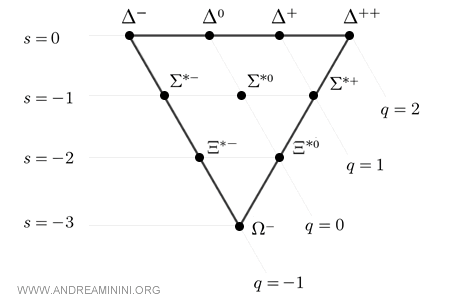
Note. The triangular layout is not merely a visual convenience. It reflects a deep physical structure: all particles in the decuplet have their spins aligned, giving a total spin of \( \tfrac32 \), and the symmetry among the quarks is maximal.

The diagram is constructed by arranging the particles according to two quantum numbers: strangeness ( $ S $ ) and electric charge ( $ Q $ ).

Moving from the top downward, the strangeness decreases, corresponding to an increasing number of strange quarks within each particle.

At the top vertex of the triangle are four $ \Delta $ baryons, which contain no strange quarks and are composed exclusively of up (u) and down (d) quarks.

• \( \Delta^{++} = uuu \)
• \( \Delta^+ = uud \)
• \( \Delta^0 = udd \)
• \( \Delta^- = ddd \)

Immediately below them appear three $ \Sigma $ baryons, each containing one strange quark (s) and two light quarks, up (u) and down (d):

• \( \Sigma^{*+} = uus \)
• \( \Sigma^{*0} = uds \)
• \( \Sigma^{*-} = dds \)

The presence of a strange quark slightly breaks the symmetry and increases the mass relative to the $ \Delta $ baryons.

Note. The asterisk indicates that the particle \( \Sigma \) is in a spin-\( \tfrac32 \) state. It belongs to the same family of \( \Sigma \) baryons found in the octet, but appears in a different spin configuration. In this case, the total spin is no longer \( \tfrac12 \) but \( \tfrac32 \), because the spins of the three constituent quarks are fully aligned. Each quark carries an intrinsic spin of \( \tfrac12 \), regardless of whether it is an up, down, or strange quark. When all three spins point in the same direction (↑↑↑), the total angular momentum of the system reaches its maximum possible value:  \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] This configuration corresponds to the spin state characteristic of the decuplet. By contrast, when the spins are not all aligned (↑↑↓, ↑↓↑, or ↓↑↑), their vector combination yields a total spin of  \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] In this case, the resulting state has spin \( \tfrac12 \) and belongs to the baryon octet. Consequently, the distinction between \( \Sigma \) and \( \Sigma^* \) does not lie in their quark content, which is identical, but solely in the way the quark spins are coupled. The same reasoning applies to the particle \( \Xi^* \), which represents the spin-\( \tfrac32 \) counterpart of the corresponding \( \Xi \) baryon in the octet.

At the next level are two $ \Xi $ baryons, composed of two strange quarks and one light quark. Their masses increase further.

• \( \Xi^{*0} = uss \)
• \( \Xi^{*-} = dss \)

Finally, at the base of the triangle lies a single particle, the $ \Omega^- $, composed entirely of strange quarks:

\[ \Omega^- = sss \]

This particle represents the lowest point of the decuplet and is characterized by strangeness -3, electric charge -1, and spin \( \tfrac32 \).

The prediction of the \( \Omega^- \) particle

The most celebrated success of this theoretical framework was the prediction of the \( \Omega^- \) particle.

This particle occupies the lowest vertex of the decuplet and completes the symmetric structure predicted by the theory, even though it had not yet been observed at the time the model was formulated.

When it was finally discovered experimentally in 1964, it provided striking confirmation of the validity of SU(3) flavor symmetry.

And so on.