Young diagrams in SU(3) symmetry

Young diagrams are a graphical device used to represent, in a compact and systematic way, the representations of the SU(3) group and to determine how these representations combine under tensor products.

In particle physics, SU(3) symmetry refers to the flavor symmetry associated with the up, down, and strange quarks ( u,d,s ).

Young diagrams are widely used to classify mesons, baryons, and particle multiplets according to their symmetry properties.

What is a Young diagram

A Young diagram consists of boxes arranged in left-aligned rows, with row lengths that do not increase as one moves from the top to the bottom.

The fundamental representation of SU(3) is depicted by a diagram with a single box. Its dimension is $ 3 $ and, from a physical standpoint, it corresponds to the quark triplet \(  \{ u,d,s \} \).

Standard examples include a single box (1), two boxes in a row (2), two boxes in a column (1,1), two boxes in the top row with one directly below (2,1), and similar configurations.

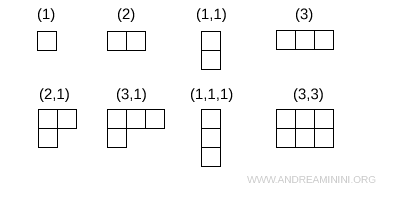
Each Young diagram specifies a distinct symmetry type for the indices of a tensor representation.

Basic rules for SU(3)

For the group SU(3), the following fundamental rules apply.

1. Each box represents a tensor index transforming according to the fundamental representation \( 3 = \{ u,d,s \} \).
2. Boxes lying in the same row indicate symmetrization of the corresponding indices.
3. Boxes lying in the same column indicate antisymmetrization of the corresponding indices.
4. The diagram must consist of rows whose lengths are non-increasing from top to bottom.
5. In SU(3), no Young diagram may contain more than three rows, since the complete antisymmetrization of four indices vanishes identically. This constraint is essential, as it automatically limits the set of admissible representations.
6. Tensor product
   In a tensor product (for example $ 6 \otimes 3 $), the boxes associated with the second factor are added one at a time to the Young diagram of the first factor. This procedure generates all diagrams that are consistent with Young’s rules. Any configuration that violates a rule must be discarded. If, at some stage, a box admits no permissible position, the corresponding channel is said to close.
   • Column antisymmetry
     In the tensor product, boxes belonging to an antisymmetric column
     1] can never all be placed in the same row
     2] may all be placed in the same column only if they extend a column already present in the original diagram 
   • Final dimension check
     The sum of the dimensions of all admissible diagrams must equal the dimension of the tensor product. For example, in $ 6 \otimes 3 $ there are $ 6 \times 3 = 18 $ states, so the sum of the resulting representations must also be 18 (for instance $ 15 \oplus 3 $ ).  If some channels close and part of the total dimension is missing, the remaining contribution is obtained by subtraction and is identified with the compatible representation.

Why are Young diagrams so useful? Young diagrams provide an immediate visual handle on symmetry properties, making it possible to identify the allowed representations and to determine which quark combinations are permitted, without lengthy algebraic manipulations. In this way, the abstract algebra of SU(3) is translated into a concrete and discrete geometric language. Young diagrams do not determine which particles exist, but rather which symmetry patterns are allowed. The group SU(3) fixes the structure, and Young diagrams offer the most transparent way to read it.

Possible multiplet combinations

To compute the dimensions of the multiplets associated with a given Young diagram in SU(3) symmetry, one uses the following formula:

\[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \]

where

• \( N \) is the dimension of the fundamental representation of the group. For example, for SU(2) one has N = 2, for SU(3) N = 3, for SU(4) N = 4, and so on.
• \( r \) is the row index of a box in the Young diagram, counted from top to bottom starting at 0.
• \( c \) is the column index of a box in the Young diagram, counted from left to right starting at 0.
• \( h \) is the hook length of the box, defined as \[ h = (\text{number of boxes to the right}) + (\text{number of boxes below}) + 1 \] where the term \( +1 \) accounts for the box itself.

The product is taken over all boxes in the Young diagram.

Note. The factor $ (c - r) $ depends only on the position of the box within the diagram, while the hook length \( h \) depends solely on the shape of the diagram. This formula is valid for any Young diagram in SU(N) and requires no additional corrections.

A practical example

Combining two quarks: \( 3 \otimes 3 \)

Consider the tensor product of two fundamental representations \( 3 = \{ u,d,s \} \).

$$ 3 \otimes 3 $$

The representation $ 3 $ is depicted by a single box carrying the indices \(  \{ u,d,s \} \).

To evaluate this tensor product using Young diagrams, a second box is added to the first in all admissible ways, subject to the rules above. Two distinct configurations arise:

1. Two boxes in a row
   The boxes lie in the same row, signaling a symmetric combination. This configuration corresponds to the representation \( 6 \).
   
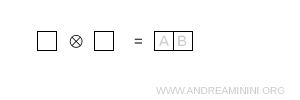   Note. To compute the dimension, I evaluate the product of the contributions from each box using \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \] Here N = 3 because the group is SU(3).
   

   • Box A. The row index is $ r=0 $, the column index is $ c=0 $. There is one box to the right and none below, hence $ h=1+0+1=2 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Box B. The row index is $ r=0 $, the column index is $ c=1 $. There are no boxes to the right or below, so $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{1} = 4 $$

   The product of these factors yields the dimension $$ dim = \frac{3}{2} \cdot 4 = 6 $$ Since the diagram is horizontal, the representation is symmetric and corresponds to $ 6 $.
2. Two boxes in a column
   The boxes are stacked vertically, signaling an antisymmetric combination. This configuration corresponds to the representation \( \bar{3} \).
   
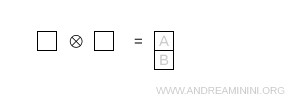   Note. The dimension is again obtained from \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \] with N = 3 for SU(3).
   

   • Box A. The row index is $ r=0 $, the column index is $ c=0 $. There are no boxes to the right and one box below, so $ h=0+1+1=2 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Box B. The row index is $ r=1 $, the column index is $ c=0 $. There are no boxes to the right or below, hence $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2 $$

   The product yields the dimension $$ dim = \frac{3}{2} \cdot 2 = 3 $$ The vertical arrangement encodes antisymmetry, so this representation is \( \bar 3 \).

The final result is therefore

quark - antiquark\[ 3 \otimes 3 = 6 \oplus \bar{3} \]

Physically, this decomposition means that the tensor product of two quark triplets splits into six symmetric quark pairs and three antisymmetric quark pairs.

Note. This outcome is fully consistent with physical intuition. A quark pair is symmetric if exchanging the two quarks leaves the state unchanged, and antisymmetric if the exchange produces an overall minus sign. For the three quark flavors ( \( u,d,s \) ), there are six symmetric pairs. \[ uu \xrightarrow{\text{exchange}} uu  \] \[ dd \xrightarrow{\text{exchange}} dd \] \[ ss \xrightarrow{\text{exchange}} ss \] \[ ud+du \xrightarrow{\text{exchange}} du+ud = ud+du \] \[ us+su \xrightarrow{\text{exchange}} su+us = us+su \] \[ ds+sd \xrightarrow{\text{exchange}} sd+ds =  ds+sd \] There are also three antisymmetric pairs. \[ ud-du \xrightarrow{\text{exchange}} du-ud = - (ud - du) \] \[ us-su \xrightarrow{\text{exchange}} su-us = - (us - su) \] \[ ds-sd \xrightarrow{\text{exchange}} sd-ds = - (ds - sd) \]

Combining three quarks: \( 3 \otimes 3 \otimes 3 \)

This is the fundamental case relevant to baryons.

$$ 3 \otimes 3 \otimes 3 $$

Starting from the previous result for $ 3 \otimes 3 $ (with two boxes arranged either horizontally or vertically), I now add a third box. The allowed Young diagrams are the following:

1. Three boxes in a row
   This is the fully symmetric configuration and it corresponds to the decuplet representation \( 10 \).
   
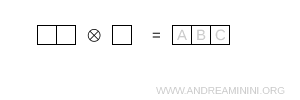   Note. The dimension is obtained by multiplying the contributions associated with each box using the formula \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \] Here N = 3.
   

   • Box A. Row index $ r=0 $, column index $ c=0 $. There are two boxes to the right and none below, hence $ h=2+0+1=3 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = 1 $$
   • Box B. Row index $ r=0 $, column index $ c=1 $. There is one box to the right and none below, so $ h=1+0+1=2 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{2} = 2 $$
   • Box C. Row index $ r=0 $, column index $ c=2 $. There are no boxes to the right or below, so $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 2 - 0}{1} = 5 $$

   The product of these factors gives the dimension $$ dim = 1 \cdot 2 \cdot 5 = 10 $$ Because the boxes are arranged horizontally, the representation is totally symmetric and corresponds to the decuplet $ 10 $.
2. Two boxes in the first row and one in the second row
   This diagram has mixed symmetry and corresponds to the octet representation \( 8 \).
   
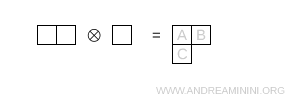   Note. The dimension is again computed using \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \] with N = 3.
   

   • Box A. Row index $ r=0 $, column index $ c=0 $. There is one box to the right and one below, so $ h=1+1+1=3 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{3} = 1 $$
   • Box B. Row index $ r=0 $, column index $ c=1 $. There are no boxes to the right or below, hence $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{1} = 4 $$
   • Box C. Row index $ r=1 $, column index $ c=0 $. There are no boxes to the right or below, so $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2 $$

   The product yields the dimension $$ dim = 1 \cdot 4 \cdot 2 = 8 $$ This Young diagram therefore corresponds to the octet representation $ 8 $.
3. Three boxes in a column
   This is the fully antisymmetric configuration and it corresponds to the singlet representation \( 1 \).
   
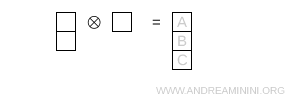   Note. Once again, I apply the formula with N = 3: \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \]
   

   • Box A. Row index $ r=0 $, column index $ c=0 $. There are two boxes below and none to the right, so $ h=0+2+1=3 $.  $$ \frac{N + c - r}{h}  = 1 $$
   • Box B. Row index $ r=1 $, column index $ c=0 $. There is one box below and none to the right, so $ h=0+1+1=2 $.  $$ \frac{N + c - r}{h}  = 1 $$
   • Box C. Row index $ r=2 $, column index $ c=0 $. There are no boxes to the right or below, so $ h=0+0+1=1 $.  $$ \frac{N + c - r}{h}  = 1 $$

   The product of the box values yields $$ dim = 1 \cdot 1 \cdot 1 = 1 $$ This corresponds to the singlet representation, which is always denoted by $ 1 $, since a one-dimensional representation is identical to its conjugate, that is $ \bar{1} = 1 $.
4. Two boxes in the first row and one in the second row
   This diagram again has mixed symmetry and corresponds to the octet representation \( 8 \).
   

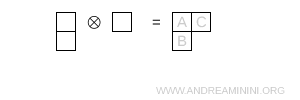
   Note. This Young diagram has the same shape as the one discussed above and therefore also corresponds to the octet representation ($ 8 $).

The final decomposition is therefore:

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

These are precisely the multiplets observed experimentally in the baryon spectrum.

Note. Each Young diagram is not merely a mathematical construct, but carries a precise physical interpretation. The decuplet (10) describes baryons with fully symmetric flavor wavefunctions, such as the \( \Delta \) states. The octet (8) corresponds to baryons with mixed flavor symmetry, including the nucleons as well as the \( \Sigma \) and \( \Xi \) baryons. The singlet (1) represents a fully antisymmetric flavor state.

Combination of two quarks: \( 3 \otimes \bar{3} \)

In this example, we evaluate the tensor product

$$ 3 \otimes \bar{3} $$

The fundamental representation \( 3 \) is depicted by a single box, while the conjugate representation \( \bar{3} \) is represented by two boxes stacked vertically, reflecting its interpretation as an antisymmetric combination of two fundamental indices in SU(3).

The calculation is performed using Young diagrams by adding the box associated with the representation \( 3 \) to the Young diagram of \( \bar{3} \). Only two Young tableaux are allowed by the rules of SU(3).

• Two boxes in a row and one below
  This Young diagram has shape (2,1) and dimension 8.
  

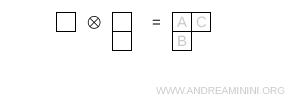
  Note. This case has already been analyzed in previous examples. It is well known that this Young diagram corresponds to the octet representation \( 8 \) of SU(3).

• Three boxes in a column
  This Young diagram has shape (1,1,1) and dimension 1.
  
  
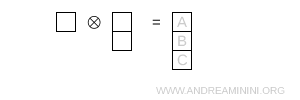
  Note. This case has also been discussed earlier. This Young diagram represents the singlet representation \( 1 \) of SU(3).

The resulting decomposition is therefore:

$$ 3 \otimes \bar{3} = 8 \oplus 1 $$

In this way, Young diagrams provide a direct explanation of why certain baryons exist and why no additional flavor multiplets are allowed within SU(3).

Combination \( 6 \otimes \bar 3 \)

I now evaluate the tensor product

$$ 6 \otimes \bar 3 $$

The representation $ 6 $ is depicted by two boxes arranged in a single row, while $ \bar 3 $ is represented by two boxes stacked in a column, reflecting its antisymmetric character.

The computation is performed using Young diagrams. In this case, only one nontrivial configuration is admissible.

• Three boxes in the first row and one in the second
  This Young diagram is of type (3,1) and has dimension $ 15 $.
  
  
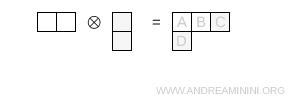
  Note. The dimension is computed using the standard hook-length formula \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \] with $ N=3 $ throughout.
  

  • Box A. The row index is $ r=0 $ and the column index is $ c=0 $. There are two boxes to the right and one below, so the hook length is $ h=2+1+1=4 $ (right+below+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 0}{4} = \frac{3}{4}  $$
  • Box B. The row index is $ r=0 $ and the column index is $ c=1 $. There is one box to the right and none below, giving $ h=1+0+1=2 $ (right+below+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 1 - 0}{2} = \frac{4}{2} = 2 $$
  • Box C. The row index is $ r=0 $ and the column index is $ c=2 $. There are no boxes to the right and none below, so $ h=0+0+1=1 $ (right+below+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 2 - 0}{1} = 5  $$
  • Box D. The row index is $ r=1 $ and the column index is $ c=0 $. There are no boxes to the right and none below, so $ h=0+0+1=1 $ (right+below+1).  $$ \frac{N + c - r}{h}  = \frac{3 + 0 - 1}{1} = 2  $$

  The resulting dimension is therefore $$ \dim = \frac{3}{4} \cdot 2 \cdot 5 \cdot 2 = 15 $$ This representation is characterized by mixed symmetry.
• No further admissible configurations
  The two boxes associated with the antisymmetric column cannot both be placed in the same row, since this would impose a symmetrization incompatible with antisymmetry. They also cannot both be placed in a column, because the initial diagram contains no column that can be extended. If only one box is added in the lower row, the second box has no admissible position, and the corresponding composition channel closes.
  
  
  Solution. In this situation, the remaining compatible representation is identified by dimension counting. The dimension of the tensor product \( 6 \otimes \bar 3 \) is \( 6 \times 3 = 18 \), so the total number of states must be 18. Since a 15-dimensional representation has already been obtained, the remainder is $$ 18 - 15 = 3 $$ Because \( 3 \) is an admissible representation of SU(3), the missing term in the decomposition is precisely \( 3 \).

The final decomposition is therefore

$$ 6 \otimes \bar 3 = 15 \oplus 3 $$

In this way, Young diagrams provide a clear and systematic framework for understanding why certain particle multiplets exist while others do not.

And so on.