Special Relativity

Special relativity is a theory introduced by Albert Einstein in 1905. It extends classical mechanics to situations where objects move at speeds approaching the speed of light in a vacuum.

Put simply, special relativity reshapes our everyday intuition about space and time, which classical mechanics treated as absolute and independent.

It introduces a unified, symmetric framework of space-time, where space and time are relative quantities that depend on the observer’s state of motion.

The two fundamental postulates

The theory is built on two experimentally verified principles:

• Principle of relativity
  The laws of physics are identical in all inertial frames of reference-that is, in frames that are not accelerating. No preferred frame exists: the equations of physics must take the same form for every observer moving at constant velocity in a straight line.
• Constancy of the speed of light
  The speed of light in a vacuum has the same value for all observers, regardless of the motion of the source or the observer. This speed is a universal constant: $$ c \approx 3 \times 10^8 \,\text{m/s} $$

Together, these postulates revolutionize the way we think about space and time, which in classical mechanics were regarded as fixed and absolute.

In particular, they lead to time dilation, length contraction, the relativity of simultaneity, and the equivalence of mass and energy.

Note. In 1915, Einstein expanded relativity to include accelerated systems and gravity, formulating General Relativity, in which space-time is curved by mass-energy. Special relativity (1905) should not be confused with general relativity (1915). Both are Einstein’s theories, but they address different domains.

Time dilation

Time dilation is the effect whereby the time measured by an outside observer is longer than the time measured in the frame where the event occurs (the rest frame of the phenomenon).

It is one of the most striking consequences of special relativity: time does not flow uniformly for all observers.

A moving clock runs slower compared with the time kept by a stationary observer.

$$ \Delta t = \gamma \cdot \Delta t_0 \quad \text{with} \quad \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

Where:

• $\Delta t_0$ is the proper time, the time measured in the frame where the clock is at rest.
  This time is intrinsic to the phenomenon itself and is said to be measured in the rest frame of the observed event.
• $\Delta t$ is the dilated time, recorded by an observer moving relative to the clock: to them, the moving clock ticks more slowly than clocks in their own frame.
• $\gamma$ is the Lorentz factor, which is always greater than 1 for $v>0$.

As the relative speed approaches the speed of light, time dilation becomes more pronounced, and time in the moving frame runs increasingly slower compared with the reference frame of the stationary observer.

For example, if $t$ is the time measured on Earth and we observe a spaceship flying close to the speed of light, the time $t'$ on board the spacecraft runs much more slowly than Earth time.

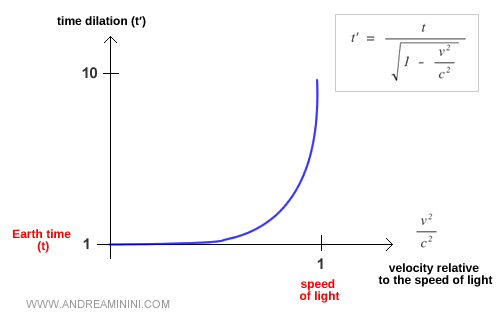
This underlies the famous twin paradox.

Two twins begin in the same frame of reference (Earth). One stays on Earth, while the other travels into space aboard a ship moving at a relativistic speed near that of light. When the traveler returns, the twins no longer share the same age:

• The twin who remained on Earth has aged more.
• The traveling twin is still younger.

This is explained by time dilation: during the journey, time on board the ship passed more slowly than time measured on Earth.

Time dilation is not just a theoretical prediction. It has been confirmed repeatedly and unambiguously in experiments, particularly in high-energy particle physics.

For instance, an unstable particle (such as a muon) travels at relativistic speeds. If its rest-frame lifetime is $ \Delta t_0 = 2.2 \,\mu s $, then for an observer on Earth watching it move at $v = 0.99 \cdot c$, nearly the speed of light, the observed lifetime is $ \Delta t = 15.6 \,\mu s $. $$ \gamma \approx \frac{1}{\sqrt{1 - 0.99^2}} \approx 7.1 $$ $$ \Delta t = 7.1 \cdot 2.2 \approx 15.6 \,\mu s $$ The muon lives longer than expected because, from its perspective, time is running more slowly.

Length contraction

Length contraction is the effect by which an object in motion appears shortened along the direction of travel compared with its length measured in its own rest frame.

A moving object appears shorter along its direction of motion than it does at rest.

$$ L = \frac{L_0}{\gamma} $$

Where:

• $L_0$ is the proper length in the frame where the object is at rest.
• $L$ is the contracted length measured by an observer for whom the object is moving.

For example, a spaceship 100 m long at rest travels at $v = 0.8 \cdot c$ relative to Earth-about 80% the speed of light. In this case, the Lorentz factor is 1.667. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{\sqrt{0.36}} = \frac{1}{0.6} \approx 1.667 $$ The spaceship in motion, as seen from Earth, is about 60 meters long. $$ L = \frac{100}{1.667} \approx 60 \,\text{m} $$ Thus, the ship appears shorter to the Earth-based observer.

The relativity of simultaneity

Two events that are simultaneous in one frame of reference may not be simultaneous in another frame moving relative to the first.

Simultaneity, therefore, is not absolute but depends on the observer’s frame.

This effect follows from Lorentz transformations, which show that space and time are inseparably linked.

For example, an observer on a moving train sees two lightning bolts strike the ends of a carriage at the same time. An observer standing on the ground does not see them as simultaneous, because the light covers different distances due to the motion of the train.

Mass-energy equivalence

Mass and energy are two expressions of the same physical quantity.

This equivalence is Einstein’s well-known law:

$$ E = mc^2 $$

Where:

• $E$ is the energy contained in the rest mass $m$.
• $c$ is the speed of light in a vacuum.

This relation underlies both nuclear power generation and nuclear weapons.

For example, one gram of mass (0.001 kg) corresponds to: $$ E = 0.001 \cdot (3 \times 10^8)^2 = 9 \times 10^{13} \,\text{J} $$ An immense amount of energy-equivalent to the explosion of several dozen tons of TNT.

And so on.