Beta Coefficient

Put simply, the beta coefficient tells us how a fundamental force (like the electromagnetic or strong force) changes when we probe shorter distances or higher energies.

It is one of the cornerstones of quantum field theory.

The beta function is defined as:

$$ \beta(g) = \mu \frac{d g}{d\mu} $$

Its physical meaning is straightforward:

• If $\beta(g) > 0$, the interaction grows stronger with energy (ultraviolet divergence).
• If $\beta(g) < 0$, the interaction weakens with energy (asymptotic freedom).

In short, the beta coefficient tracks how a force changes with energy.

Example. In QED the beta coefficient is positive, since the electromagnetic interaction grows with energy (screening). In QCD, however, the beta coefficient is negative: the strong force weakens at high energies (anti-screening). This distinction underlies key ideas in modern physics such as confinement, asymptotic freedom, and the running of the fundamental constants of nature.

Example

In Quantum Electrodynamics (QED) the beta coefficient is positive:

$$ \beta(\alpha) > 0 $$

This means the effective charge increases with energy, producing what is known as vacuum screening.

At very short distances (high energies), the photon sees less polarization, so the charge appears larger.

At longer distances, polarization effects build up and the effective charge is reduced.

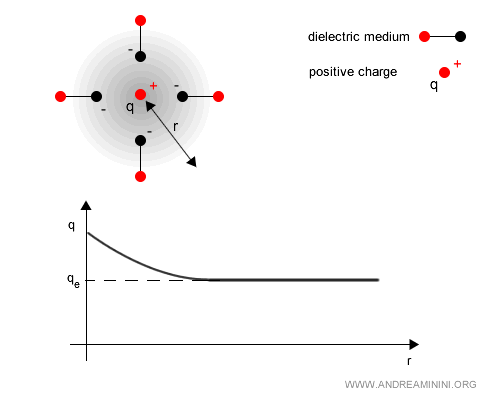
Example. The quantum vacuum behaves like a dielectric medium: fluctuations create virtual electron - positron pairs that polarize in the presence of a charge $ q $. For a positive charge, the negative components of the pairs are drawn in, while the positive ones are repelled. This polarization diminishes the electric field strength at large distances, making the effective charge $q_e(r)$ appear smaller than the bare charge $q$. In other words, the real charge is “screened.”

 

Example 2

In Quantum Chromodynamics (QCD) the beta coefficient is negative:

$$ \beta(g_s) < 0 $$

This implies that the coupling constant decreases with energy, giving rise to anti-screening.

At very short distances (high energy), quarks behave almost as if they were free (asymptotic freedom).

Conversely, as they separate, the coupling grows and quarks remain confined within hadrons (e.g., protons or neutrons). This is the phenomenon of quark confinement.

The Beta Function in QCD

At one loop, the QCD beta function is:

$$ \beta(g_s) = - \left( \frac{11}{3} N_c - \frac{2}{3} n_f \right) \frac{g_s^3}{16\pi^2} $$

Where:

• $N_c = 3$ is the number of colors
• $n_f$ is the number of quark flavors
• $g_s$ is the strong coupling constant

The term $\frac{11}{3}N_c$ comes from virtual gluons, which strengthen the interaction at long distances (anti-screening).

The term $\frac{2}{3}n_f$ comes from virtual quark loops, which instead screen the interaction, much like in QED.

As long as $n_f < \frac{11}{2}N_c$, the coefficient $ \beta(g_s) $ remains negative.

Note. With three colors $ N_c = 3 $, the condition becomes: $$ n_f < \frac{11}{2} \cdot 3 = 16.5 $$ Thus, the behavior depends on the number of flavors $ n_f $. If there were too many, the quark contribution would dominate, $ \beta > 0 $, and asymptotic freedom would be lost.

In reality, there are $ n_f=6 $ flavors, so $n_f < 16.5$, and the QCD beta coefficient is indeed negative:

$$ \beta(g_s) < 0 $$

This means $g_s$ decreases as the energy scale increases.

In other words, in QCD the strong force weakens at very short distances.

This phenomenon is what we call asymptotic freedom.

Note. This is precisely why, in ultra-high-energy collisions such as those at CERN, quarks appear almost free: their interaction diminishes the closer we probe (equivalently, at higher energies).

A Simplified Expression

In QCD, the one-loop beta function can be expressed in a compact form (in suitably scaled units):

$$ \beta(g) \sim -\left(11n - 2f\right) $$

Where $n = N_c$ (the number of colors) and $f = n_f$ (the number of flavors).

In many references, this is often written as:

$$ \beta \propto -(11n - 2f) = 2f - 11n $$

or simply:

$$ \beta \sim (2f - 11n) $$

Gluons contribute the $11N_c$ term (anti-screening), while quarks (flavors) contribute the $-2n_f$ term (screening, as in QED).

In QCD the beta function is negative whenever $11n > 2f$, the condition that guarantees asymptotic freedom.

Note. This compact form is useful when analyzing general patterns, particularly for arbitrary $N_c, n_f$ (e.g., in supersymmetric models or higher-dimensional theories), as it highlights the competition between gluon and quark contributions to the beta function.

And so on.