Central Symmetry
Central symmetry is a geometric transformation that maps each point A of a figure to a point A' relative to a fixed point P, chosen as the center of symmetry. This is done in such a way that P becomes the midpoint of the segment connecting A and A'.
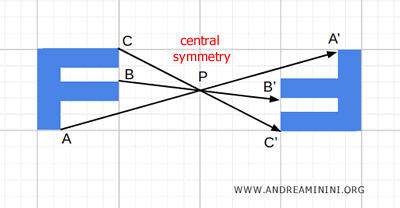
Central symmetry is an isometry because it preserves the distances between points within a figure.
This transformation can be applied both in a plane and in three-dimensional Euclidean space.
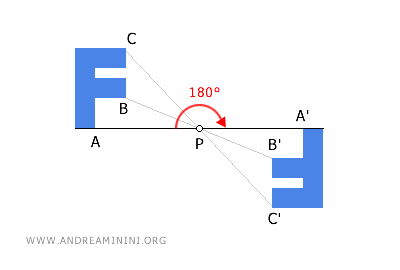
In the plane, central symmetry can be viewed as a 180° rotation around a center of symmetry. In three-dimensional space, it acts as a reversing isometry.
A Practical Example
Central symmetry is a geometric transformation that operates around a fixed point known as the center of symmetry.
This point, labeled P, serves as the anchor for the transformation.
For example, imagine drawing a figure on a plane and selecting a fixed point P as the center of symmetry.
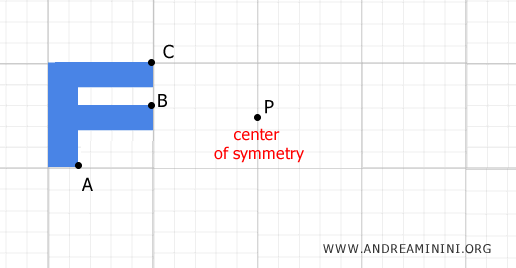
Now, consider points A, B, and C of the figure.
Next, draw rays starting from each of these points (A, B, C) and passing through the center of symmetry P.
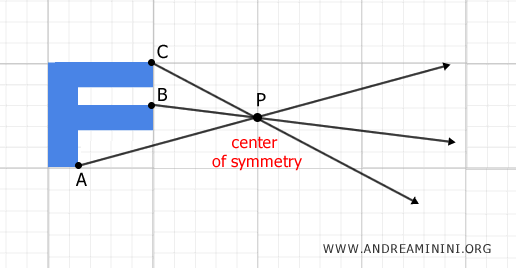
At this point, each point of the figure is mapped to a corresponding point in such a way that P becomes the midpoint of the segment connecting them.
For example, consider point A. The corresponding point A' is located along the same line, at the same distance from P as A, but in the opposite direction.
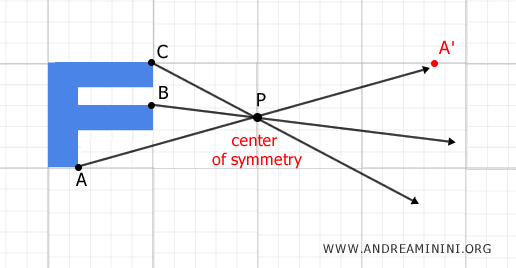
These two points, A and A', are known as symmetric points with respect to point P.
The center of symmetry, P, is exactly at the midpoint of segment AA'. In other words, the segment AA' is bisected by point P.
$$ \overline{AP} \cong \overline {A'P} $$
Repeating this process for all the points of the figure results in a figure that is rotated by 180°.
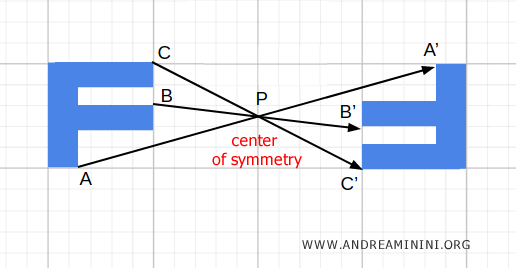
Note: Another way to visualize central symmetry in the plane is to think of rotating a figure 180° around its center of symmetry, P. This transformation produces a figure that is a mirror image of the original but remains congruent to it, as the distances between points are preserved.
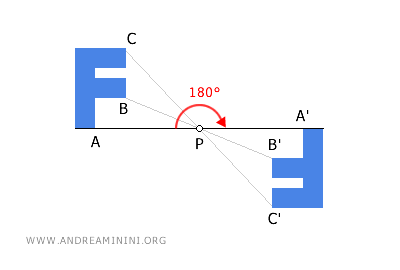
Figures obtained through central symmetry are always congruent to each other, as they maintain the same shape and size, even though their orientation in space might differ.
Because it preserves the distances between points, central symmetry is classified as an isometry.
The Equations
In the plane, the central symmetry of any point P(x;y) with respect to another point C(x0;y0) chosen as the center of symmetry can be determined using the following equations:
$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$
Note: If the origin of the Cartesian coordinate system O(0;0) is chosen as the center of symmetry, the central symmetry is simply obtained by taking the opposite coordinates of each point. In this case, x0=0 and y0=0. Therefore, if the center of symmetry is the origin, two points symmetric with respect to the origin of the Cartesian axes have opposite coordinates: $$ \begin{cases} x' = - x \\ \\ y' = - y \end{cases} $$
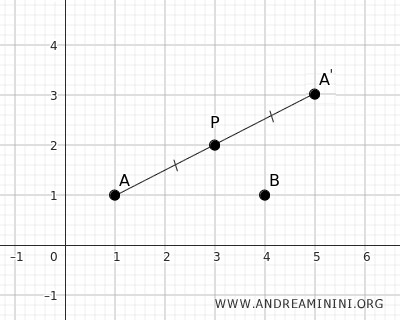
For example, let's choose the point P with coordinates P(x0;y0)=(3;2) as the center of symmetry.
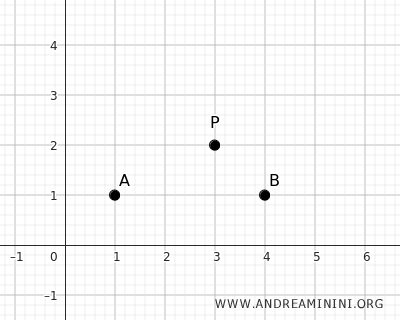
Next, add two points A(1;1) and B(4;1) on the plane.
We use the equations to calculate the corresponding point A'
Point A is at coordinates x=1 and y=1, while the center of symmetry is at coordinates x0=3 and y0=2.
$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$
$$ \begin{cases} x' = 2 \cdot 3 - 1 \\ \\ y' = 2 \cdot 2 - 1 \end{cases} $$
$$ \begin{cases} x' = 6 - 1 \\ \\ y' = 4 - 1 \end{cases} $$
$$ \begin{cases} x' = 5 \\ \\ y' = 3 \end{cases} $$
The corresponding point A' is therefore at coordinates x'=5 and y'=3.
The center of symmetry P is the midpoint of segment AA'.
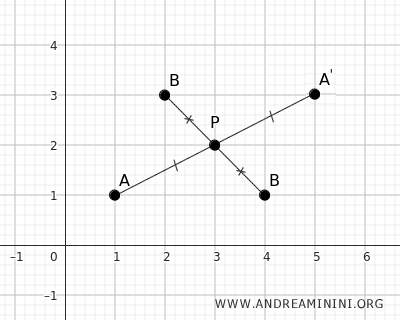
Now let's use the equations to calculate the corresponding point B'
Point B is at coordinates x=4 and y=1, and the center of symmetry remains at coordinates x0=3 and y0=2.
$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$
$$ \begin{cases} x' = 6 - 4 \\ \\ y' = 4 - 1 \end{cases} $$
$$ \begin{cases} x' = 2 \\ \\ y' = 3 \end{cases} $$
So, point B' is at coordinates x'=2 and y'=3.
The center of symmetry P is the midpoint of segment BB'.
Note that both central symmetries can be understood as a 180° rotation of points A and B around point P.
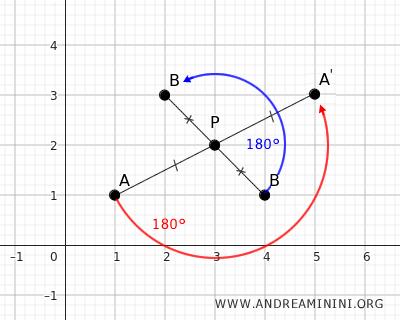
At the end of the transformation, the distance between points A' and B' remains the same.
Proof: Central symmetry is a geometric transformation that maps each point P(x;y) in the plane to another point P'(x';y'), known as the image of P with respect to a point M(xM;yM) chosen as the center of symmetry. If we draw a segment between the two points P and P', the point M is the midpoint of that segment. Therefore, we can express point M's coordinates using the midpoint formula: $$ \begin{cases} x_M = \frac{x+x'}{2} \\ \\ y_M = \frac{y+y'}{2} \end{cases} $$ From these equations, we can algebraically derive the coordinates (x';y') of the image P' of any point P(x;y) in the plane with respect to the center of symmetry M(xM;yM). $$ \begin{cases} x' = 2x_M - x \\ \\ y' = 2y_M-y \end{cases} $$ In the special case where the center of symmetry is the origin M(xM;yM)=(0;0), substituting xM=0 and yM=0 into the previous formula gives us the equations for central symmetry with respect to the origin of the plane: $$ \begin{cases} x' = - x \\ \\ y' = -y \end{cases} $$
Central Symmetry in Space
Central symmetry about a point \( O \) in space is a geometric transformation that:
- leaves point \( O \) unchanged
- maps each point \( P \), distinct from \( O \), to a point \( P' \) such that \( O \) is the midpoint of segment \( PP' \), meaning \( OP \cong OP' \)
Here’s a practical example:
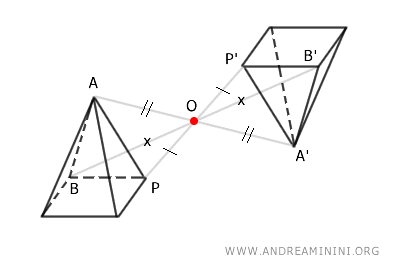
In this transformation, the central point \( O \) is the only fixed point—meaning it remains unchanged.
Two solids that are related by central symmetry about \( O \) are generally inversely congruent.
Note: Two solids are inversely congruent if they have the same shape and size but are mirror images of each other, meaning they cannot be aligned through rigid motion in space without flipping.
Key Observations
Here are some important observations about central symmetry:
- The figure obtained through central symmetry is congruent to the original figure
Central symmetry is an isometry, meaning it preserves the distances between points within a figure. This results in figures that have congruent sides and angles, and are therefore congruent to each other. Consequently, the relative distance between points is an invariant of central symmetry.
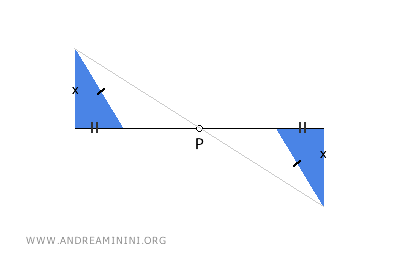
- Invariants of central symmetry
The position of the center of symmetry, P, within the plane is an invariant of central symmetry. Another invariant is the direction of the lines. Additionally, the relative distances between points in the figure are preserved. - The composition of two central symmetries with the same center results in identity
If you apply a sequence of two central isometric transformations with the same center P to a figure, one after the other, the figure will return to its original position and shape, as if no transformation had occurred. This means the composition is an involutory transformation.
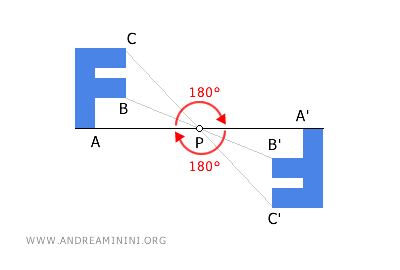
Generally, the composition of an even number of central symmetries with the same center always results in an identity transformation. - Central symmetry is not a closed operation
In general, the composition of two or more central symmetries does not necessarily produce another central symmetry. Therefore, central symmetry is not a closed operation. For instance, this composition of central symmetries with centers P and P' results in a translation of the original figure downward. As a result, the final transformation is not a central symmetry.
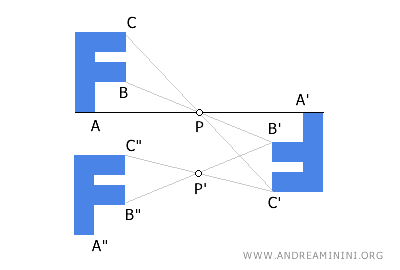
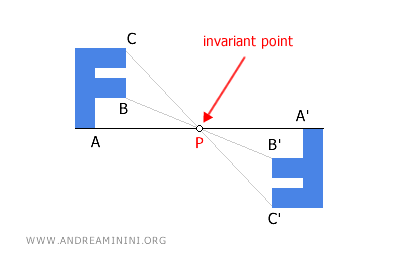
- The center of symmetry is a fixed point and is unique
In central symmetry, the center of symmetry is a point that remains unchanged in position on the plane after the transformation. It maps onto itself, making it a "fixed point" (or "invariant point"). This indicates that the position of the center is an invariant of central symmetry. Moreover, it is also the only possible fixed point in central symmetry.
- In central symmetry, lines remain parallel
Any line reflected with respect to a center of symmetry has a parallel line as its image. Therefore, the parallelism of lines is an invariant of central symmetry.
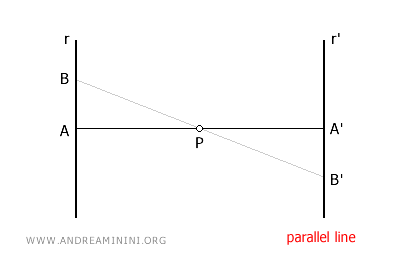
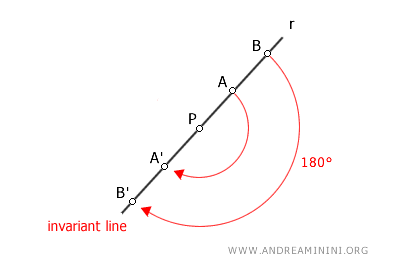
- Any line passing through the origin is a fixed line
In central symmetry, any line passing through the origin coincides with its image. As a result, it is a "fixed line" (or "invariant line") because it occupies the same points in the plane.
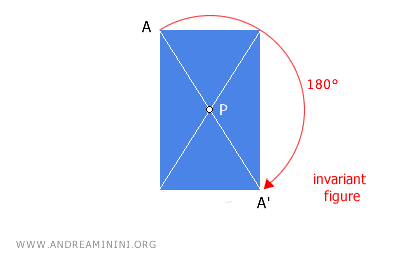
- The center of symmetry of a figure
A point in the plane is called the center of symmetry of a figure if, when chosen as the center of central symmetry, it produces a figure that occupies the same points in the plane as the original. In other words, it is a central point (if one exists) that makes the figure "fixed" with respect to central symmetry. Examples include the center of a rectangle, square, rhombus, circle, etc.
And so on.
