Isometry

Isometry is a geometric transformation that preserves the distances between points.

In simpler terms, if two points have a certain distance between them before the transformation, that distance remains unchanged afterward.

This implies that every isometry maps a figure onto a congruent figure.

Consequently, isometries also preserve surface equivalence.

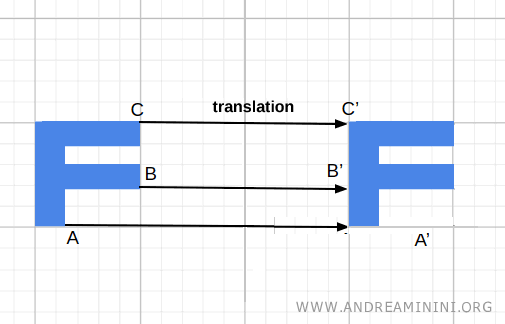
Example

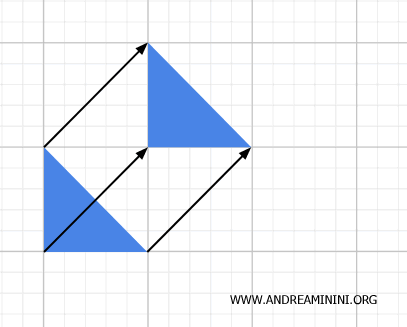
Consider a triangle that is rotated 90° clockwise and then translated to the right. The distances between points A, B, and C remain unchanged.

Both the rotation and the translation are examples of isometric transformations.

The two triangles are congruent, since their corresponding side lengths are equal. As a result, they also have the same area.

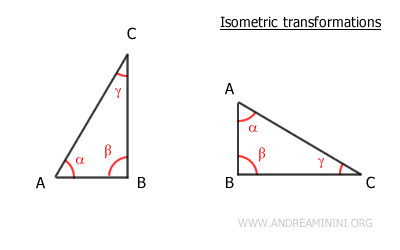
The term 'isometric' is often used interchangeably with 'congruent'. The word has Greek origins, where 'isos' means 'same' and 'metros' means 'measure'. For example, the two triangles mentioned earlier are congruent because their sides and angles remain congruent even after rotation and translation.

Transformations that result in an isometry are called isometric transformations or rigid transformations (or rigid motions) because they do not alter the shape or size of objects.

Shapes that remain unchanged under isometry are called isometric figures, as they retain the same measurements.

Types of Isometries

The main types of isometric transformations are:

• Translation
  Every point is moved by a fixed amount in a specific direction.
  
• Rotation
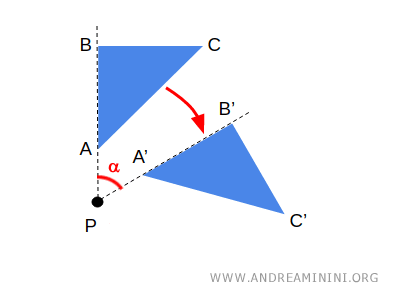
  Every point rotates around a fixed point known as the center of rotation.
  
• Reflection
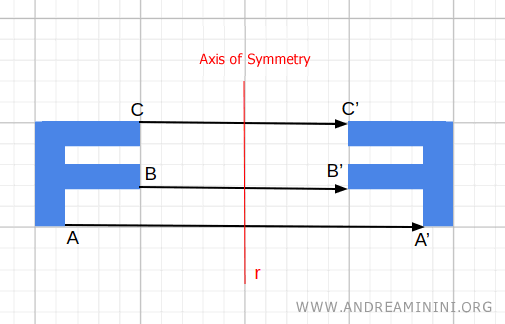
  Every point is reflected across a line, called the axis of reflection.
  
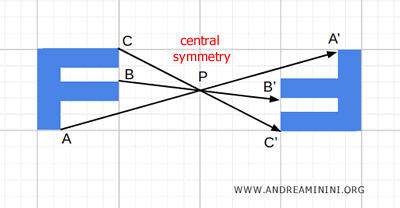
• Central Symmetry
  Every point is mapped to its diametrically opposite point relative to a central point.
  

Compositions of Isometries

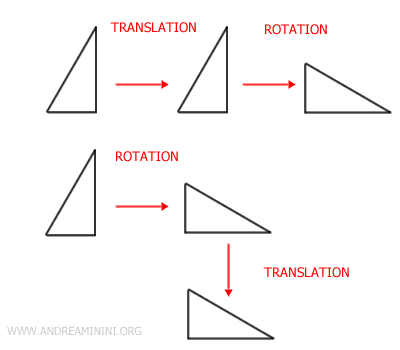
When you apply two or more isometric transformations in a specific sequence to a geometric figure, the final result can be described as a composition of isometries.

For example, you can translate a triangle 10 cm along a horizontal line (translation) and then rotate it 180° (rotation).

It's important to note that the composition of two isometries is still an isometry.

Since each isometry individually preserves distances and shapes, a composition of isometries will also retain these properties.

In other words, a figure subjected to a composition of isometries maintains its original shape and size.

Note: However, the composition of isometries is not always commutative. This means the order in which you perform the geometric transformations can affect the final result. For example, a rotation followed by a translation yields a different result than a translation followed by a rotation.

Isometric compositions can have specific names depending on the transformations combined. For example:

• Glide Reflection
  The combination of a reflection and a translation is known as a "glide reflection".
• Rototranslation
  The combination of a rotation and a translation is referred to as a "rototranslation".

Direct and Indirect Isometries

Isometries can be classified as either direct or indirect.

• Direct Isometries
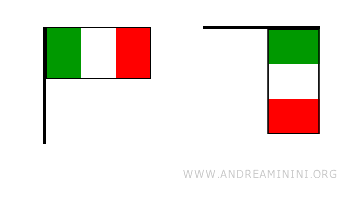
  Direct isometries preserve the orientation of a figure. In other words, when a figure undergoes a direct isometry, its clockwise or counterclockwise orientation remains unchanged. Examples of direct isometries include translations and rotations. To illustrate, these two flags can be perfectly aligned using a combination of two rigid motions (rotation + translation). This is an example of a direct isometry.
  
• Indirect Isometries
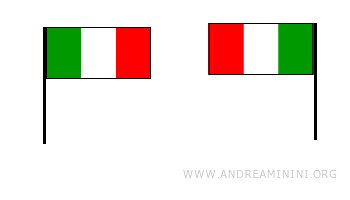
  Indirect isometries reverse the orientation of a figure and include only reflections, such as axial symmetry. This means that a figure transformed by an indirect isometry switches from clockwise to counterclockwise orientation, or vice versa. For instance, these flags can only be perfectly aligned after a reflection, as the transformation "mirrors" the figure. This is an example of an indirect isometry.
  

Note: A common mistake is assuming that an indirect isometry must always result from two rigid motions, whereas in reality, a single reflection is enough to reverse orientation. Therefore, the number of geometric transformations in a composition does not determine whether a figure is direct or indirect, only the overall effect on the figure's orientation matters.

Invariants in Isometry

In an isometry, certain characteristics of a shape may change, such as its position, while others remain unchanged.

The features that do not change are known as "invariants" in isometry.

The main invariant properties during an isometry are:

• Distance between points
  In isometries, the distance between points remains unchanged. This means that, for example, if the distance between two points A and B is 5 cm in the original figure, it will remain the same in the resulting figure after an isometric transformation.
• Length of segments
  The length of segments does not change between the original figure and its image. For instance, the segments AB, BC, and AB have the same length in both triangles.
• Angle measures
  The measure of the angles remains constant after an isometry. For example, the angles α, β, and γ of the triangle maintain the same measure after the isometric transformation.
• Area of the figure
  The total area of the figure does not change. For example, the area of the triangle remains the same after the isometric transformation.
• Shape and size
  In an isometry, the shape and size of the geometric figure do not change. These properties are invariant.
• Alignment of points
  If two or more points are aligned in the original figure, they will also be aligned in its image. For example, points A and B are aligned in both the original triangle and the resulting triangle after the transformation.
• Parallelism of lines
  Lines that are parallel in the original figure remain parallel in the image.
• Perpendicularity of lines
  Lines that are perpendicular in the original figure maintain this characteristic in their image as well. For example, segments AB and BC are perpendicular in both the first triangle (original) and the second triangle (isometric image).

Isometries in Space

Isometries in space are transformations that preserve the distances between corresponding points, keeping the shape and size of solids unchanged while altering only their position and/or orientation.

In two-dimensional geometry, isometric transformations include translations, rotations, and reflections - the same applies in three-dimensional space.

Isometries in space share the same fundamental properties as those in the plane:

• They preserve the distances between corresponding points.
• They transform each segment into a congruent segment of the same length.
• They maintain the angles between segments and between planes.

Two solids are considered congruent if they have the following identical characteristics: corresponding edges of equal length, corresponding angles of the same measure, congruent corresponding edges and faces, and equal corresponding dihedral angles.

• Directly congruent solids
  Two solid figures are directly congruent if they can be perfectly aligned using rigid motions such as translations and rotations, without requiring reflection.

  Example: Two identical cubes that can be aligned through translation and/or rotation.

• Inversely congruent solids
  Two solid figures are inversely congruent if they can be perfectly aligned only by introducing a reflection.

  Example: A right shoe and a left shoe. They have the same shape but are mirror images of each other, requiring reflection to match.

Isometries in Analytic Geometry

In analytic geometry, every isometry of the plane (translations, rotations, reflections, central symmetries, glide reflections, etc.) can be described as an affine transformation of the form

$$ \begin{cases} x' = ax + by + c \\ y' = a'x + b'y + c' \end{cases} $$

Here, the matrix $\begin{pmatrix} a & b \\ a' & b' \end{pmatrix}$ represents the linear part of the transformation, while the vector $(c, c')$ corresponds to a possible translation.

Thus, every planar isometry can be expressed using linear equations of the first degree in $x$ and $y$.

The linear coefficient matrix is always an orthogonal matrix, which means it satisfies

$$ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix}^{T} \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} = I \, . $$

Moreover, the determinant of an isometry’s linear matrix is always $\pm 1$:

$$ \det \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} = ab' - a'b = \pm 1 . $$

Accordingly, plane isometries fall into two broad classes:

• Direct isometries
  If the determinant is $+1$, the orientation is preserved. This class includes translations, rotations, and central symmetries.
• Opposite isometries
  If the determinant is $-1$, the transformation reverses orientation. This group includes reflections and glide reflections.

In all cases, the analytic structure is the same: an orthogonal linear part, possibly combined with a translation component.

Example 1

A $90^\circ$ counterclockwise rotation in the Cartesian plane is given by

$$ \begin{cases} x' = -y \\ y' = x \end{cases} $$

Its linear matrix is

$$ A = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}, \quad \det(A) = 0 \cdot 0 - (-1)\cdot 1 = +1 . $$

Since the determinant is positive, this transformation is a direct isometry.

For instance, applying the rotation to the point $P(2,1)$ yields $$ P(2,1) \;\;\longrightarrow\;\; P'(x',y') = (-1,2). $$

Example 2

Reflection across the $y$-axis can be expressed as:

$$ \begin{cases} x' = -x \\ y' = y \end{cases} $$

The associated linear matrix is

$$ A = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}, \quad \det(A) = (-1)\cdot 1 - 0 = -1 . $$

The negative determinant indicates that this is an opposite isometry.

For example, applying this reflection to the point $Q(3,2)$ gives $$ Q(3,2) \;\;\longrightarrow\;\; Q'(-3,2). $$

Additional Observations

Here are some additional observations and side notes on isometries:

• Isometries are congruences
  Isometries are geometric transformations that produce congruent figures because they preserve segment lengths and angle measures. As a result, the transformed figures are point-for-point superimposable onto the original figures after some rigid motions, fulfilling the definition of congruence in Euclidean geometry.
• Isometries are a specific type of similarity
  Isometries are similarities with a similarity ratio of 1. They satisfy all the properties of similarities:
  • they preserve the parallelism between segments,
  • corresponding angles are congruent, and
  • corresponding segments are congruent.
  Therefore, in an isometry, the shape of the figure does not change, which is an invariant property (as in similarities), because the angles remain congruent. Additionally, the corresponding segments have the same length, meaning they are proportional with a ratio of 1.
• Identifying isometries through fixed points
  The nature of an isometry can be determined by analyzing its fixed points.
  • Exactly one fixed point
    Having a single fixed point occurs only in the cases of rotation or central symmetry. In these transformations, the fixed point is, respectively, the center of rotation or the center of symmetry.
    
  • All points fixed
    If every point remains fixed, the transformation is a reflection. The axis of symmetry is a line of fixed points, every point on that line is unchanged.
    
  • No fixed points
    The absence of fixed points characterizes translations and glide reflections, since these isometries leave no point unmoved.
    
• The group of isometries
  The set of all isometries, under the operation of composition, forms a group because composition is associative, there is an identity transformation, and every isometry has an inverse.

And so on.