Composing Geometric Transformations
Composing geometric transformations means applying two or more transformations in a sequence to the same object. $$ s \circ t $$
It is read as "s composed with t", where t is the first transformation applied, followed by s. Therefore, composition is interpreted from right to left.
A Practical Example
For example, let's start with an initial geometric figure.
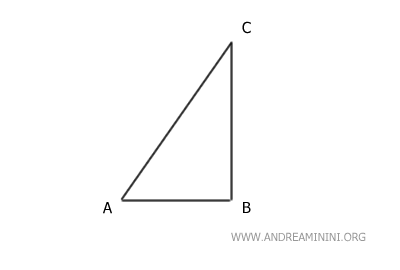
First, we apply a 90° rotation around the center of rotation, point A.
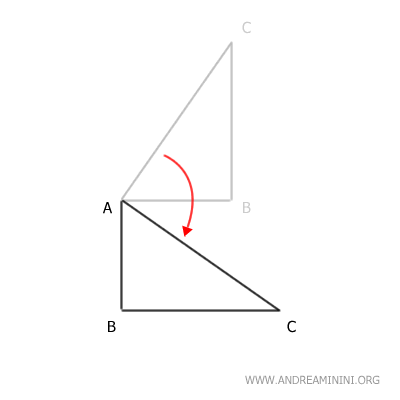
Next, we apply the second transformation to the result. For instance, a translation along the segment AB.
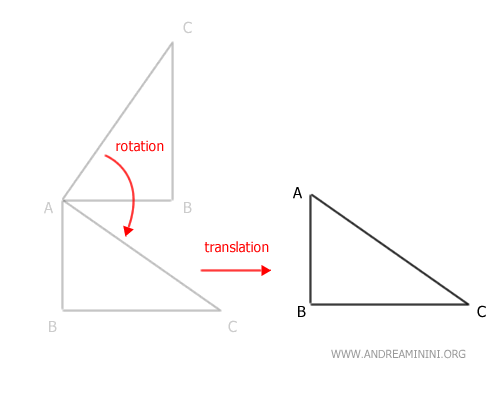
The final outcome is the composition of these two geometric transformations.
Note: A geometric transformation changes a figure according to specific rules, without altering certain fundamental properties. Examples of geometric transformations include translations, rotations, reflections, and dilations.
It's important to note that the composition of geometric transformations is not commutative.
Therefore, the order in which the transformations are applied is crucial, as it can greatly influence the final result.
Composing Transformations in Space
Geometric transformations can also be combined when applied to solid figures in space.
When I apply a geometric transformation to a figure, it produces a new transformed shape. If I then apply another transformation to this new shape, I get a final transformed figure.
Example
Let's start with a solid figure in space, \( \mathcal{F} \), such as a square-based pyramid. First, I apply a translation, which I'll call transformation \( t_1 \). This results in a new solid, \( \mathcal{F}_1 \).
Next, I apply a reflection across a plane as the second transformation, \( t_2 \), producing yet another transformed solid, \( \mathcal{F}_2 \).
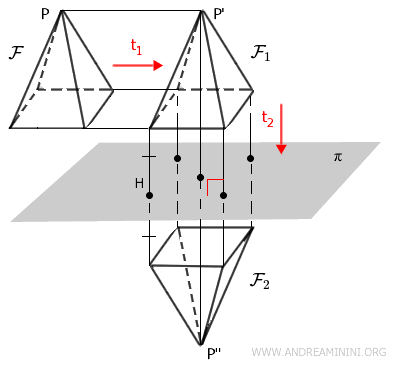
This sequence of transformations is an example of a composite transformation, \( t_2 \circ t_1 \), where \( t_1 \) is applied first, followed by \( t_2 \).
Rather than performing each step separately, I can directly apply the composite transformation \( t_2 \circ t_1 \) to the original solid \( \mathcal{F} \), arriving at the final shape \( \mathcal{F}_2 \).
Note: In three-dimensional space, the order of geometric transformations matters, as composition is generally not commutative. In other words, applying two transformations in a different order can lead to entirely different results.
Composing Transformations in Analytic Geometry
Given two transformations $t_1$ and $t_2$, the composition $t_2 \circ t_1$ is defined as: $$(t_2 \circ t_1)(P) = t_2(t_1(P))$$ where $P$ is any point in the plane.
In other words, you first apply the inner transformation $t_1$ to $P$, which gives $P_1 = t_1(P)$. Then, you apply $t_2$ to $P_1$, obtaining the final image $P_2 = t_2(P_1)$.
So if $t_1: (x, y) \mapsto (x', y')$ and $t_2: (x', y') \mapsto (x'', y'')$, the composition $t_2 \circ t_1$ becomes:
$$ t_2 \circ t_1 : (x, y) \mapsto (x'', y'') = t_2(t_1(x, y)) $$
As previously noted, composition is generally not commutative, meaning the order in which you apply the transformations matters:
$$ t_2 \circ t_1 \ne t_1 \circ t_2 $$
However, the associative property does hold:
$$ t_1 \circ ( t_2 \circ t_3 ) = ( t_1 \circ t_2 ) \circ t_3 $$
This means that grouping the transformations differently doesn't affect the final result.
Whether you first compose $t_2$ and $t_3$ and then apply $t_1$, or first compose $t_1$ and $t_2$ and then apply that result to $t_3$, the overall transformation remains the same.
Note: When you compose a transformation $t_1$ with its inverse $t_1^{-1}$, the result is the identity transformation, which leaves every point unchanged: $$ t_1 \circ t_1^{-1} = t_1^{-1} \circ t_1 = i $$ In this special case, the composition is commutative.
Example
Consider the following two transformations in the Cartesian plane:
Transformation $t_1$ reflects a point across the $x$-axis:
$$ t_1: \begin{cases} x' = x \\ y' = -y \end{cases} $$
Transformation $t_2$ translates a point 2 units to the right and 3 units up:
$$ t_2: \begin{cases} x'' = x' + 2 \\ y'' = y' + 3 \end{cases} $$
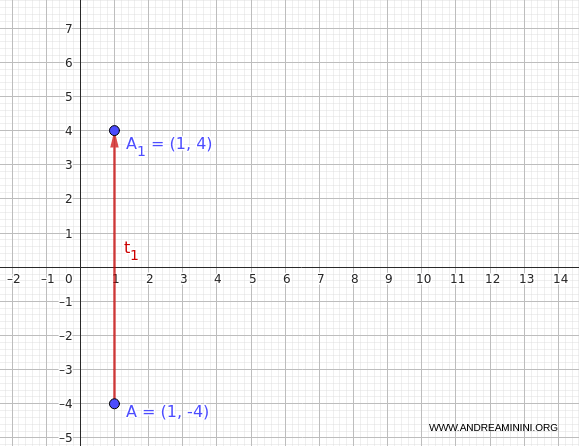
Let’s take the point $A(1, -4)$ as our starting point.
We now compute the composition $t_2 \circ t_1$, meaning we apply $t_1$ first, followed by $t_2$.
Applying $t_1$ to $A(1, -4)$ gives:
$$ A_1 = t_1(1, -4) = (1, 4) $$
Next, applying $t_2$ to $A_1(1, 4)$ yields:
$$ A_2 = t_2(1, 4) = (1 + 2, 4 + 3) = (3, 7) $$
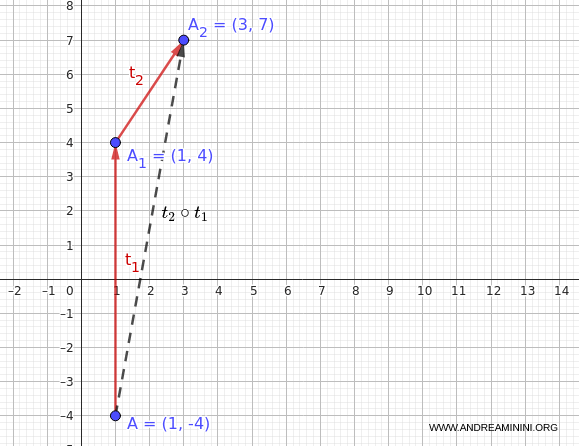
Thus, the composition $t_2 \circ t_1$ applied to $A$ results in the point $(3, 7)$:
$$ (t_2 \circ t_1)(A) = (3, 7) $$
Note: By merging the two transformations into a single operation, the composition becomes: $$ t_2 \circ t_1 : \begin{cases} x'' = x + 2 \\ y'' = -y + 3 \end{cases} $$
Example 2
Let’s take the same two transformations and the same starting point $A(1, -4)$:
$$ t_1: \begin{cases} x' = x \\ y' = -y \end{cases} $$
$$ t_2: \begin{cases} x'' = x' + 2 \\ y'' = y' + 3 \end{cases} $$
This time, we compute the composition in reverse order:
$$t_1 \circ t_2$$
That is, we apply $t_2$ first, followed by $t_1$.
Applying $t_2$ to $A(1, -4)$ gives:
$$ B_1 = t_2(1, -4) = (1 + 2, -4 + 3) = (3, -1) $$
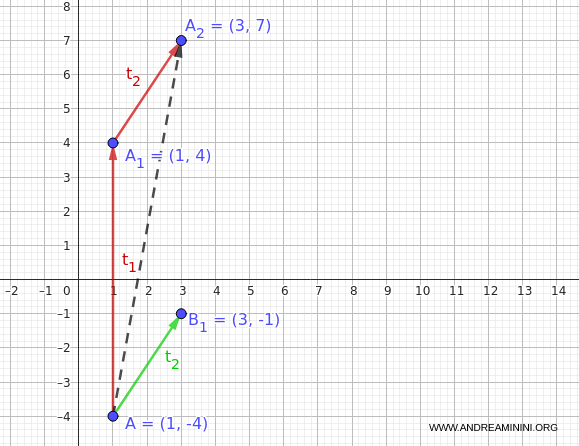
Then, applying $t_1$ to $B_1(3, -1)$ results in:
$$ B_2 = t_1(3, -1) = (3, 1) $$
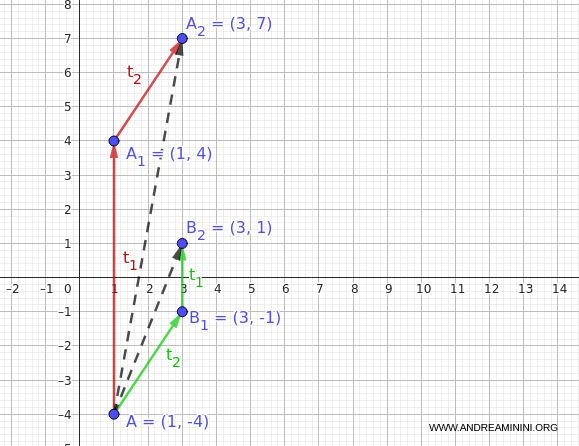
So, the composition $t_1 \circ t_2$ applied to $A$ gives the point $(3, 1)$:
$$ (t_1 \circ t_2)(A) = (3, 1) $$
Note: The two compositions (red and green) yield different results: $$(t_2 \circ t_1)(A) = (3, 7)$$ $$(t_1 \circ t_2)(A) = (3, 1)$$ This confirms that composition is not commutative in general: $$ t_2 \circ t_1 \ne t_1 \circ t_2 $$
Example 3
Now consider the transformation $t_1$, which translates a point by +4 along the $x$-axis and -2 along the $y$-axis:
$$ t_1: \begin{cases} x' = x + 4 \\ y' = y - 2 \end{cases} $$
The inverse transformation $t_1^{-1}$ should cancel out the effect of $t_1$:
$$ t_1^{-1}: \begin{cases} x'' = x' - 4 \\ y'' = y' + 2 \end{cases} $$
We now compose the two transformations:
$$t_1^{-1} \circ t_1$$
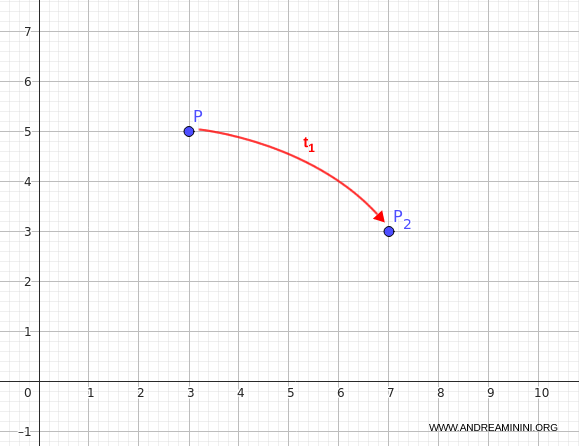
Take any point, say:
$$ P(3, 5) $$
Applying $t_1$ to $P$ gives:
$$ P_2 = t_1(3, 5) = (3 + 4, 5 - 2) = (7, 3) $$
Now apply $t_1^{-1}$ to $P_2$:
$$ t_1^{-1}(7, 3) = (7 - 4, 3 + 2) = (3, 5) $$
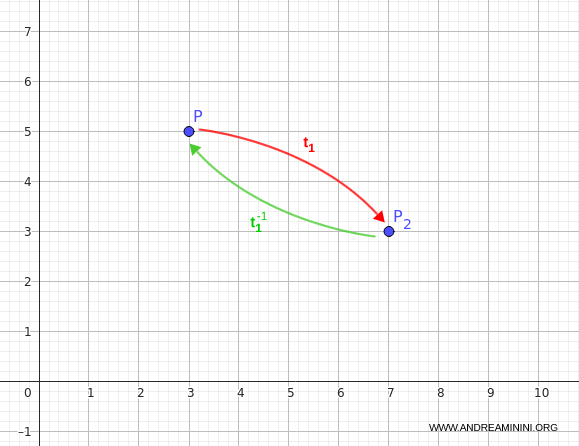
So, the composition brings us back to the original point:
$$ (t_1^{-1} \circ t_1)(3, 5) = (3, 5) $$
This confirms that composing a transformation with its inverse yields the identity transformation, which leaves every point in the plane unchanged:
$$ t_1^{-1} \circ t_1 = \text{id} $$
And so on.
