Rotation
Rotation is a geometric transformation in the plane, where every point of a figure moves around a fixed point known as the center of rotation.
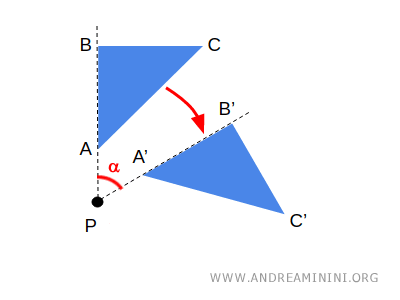
In the plane, a rotation r(P;α) with center P and angle α maps each point A to a new point A', such that segment PA is congruent to segment PA', and the angle APA' is congruent to the rotation angle α and has the same orientation.
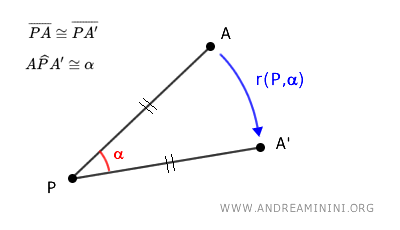
In other words, rotation is a transformation that moves the points (A) of a figure around a center of rotation (P) without changing the figure’s shape or size.
The figure resulting from a rotation is congruent to the original, meaning they have the same shape and size. Because rotation preserves the distances between points, it is classified as an isometry.
Characteristics of Rotation
Every rotation is characterized by the following elements:
- The center of rotation
- The angle of rotation
- The direction of rotation
The center of rotation is the point P around which the figure rotates.
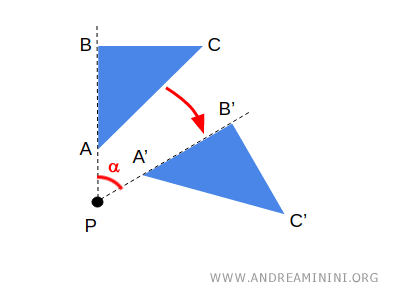
During this transformation, each point of the figure rotates by a specific angle, α, while maintaining its distance from the center of rotation.
$$ \overline{PA} \cong \overline{PA'} $$
$$ \overline{PB} \cong \overline{PB'} $$
So, the center is the only fixed point of the rotation.
The angle formed by the arc traced by the points is congruent to the rotation angle α.
$$ APA' \cong \alpha $$
$$ BPB' \cong \alpha $$
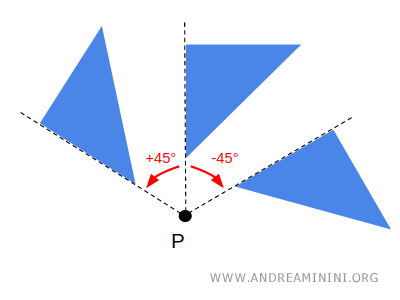
The angle of rotation is the angle α that indicates how much a point on the figure is rotated around the center of rotation.
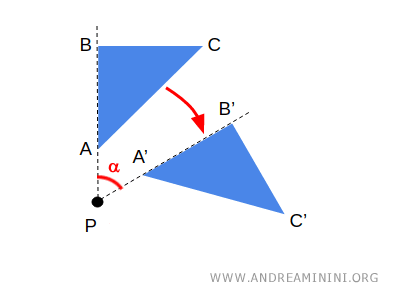
This is an oriented angle, so it’s important to specify the direction of rotation as well.
The direction of rotation can be either clockwise or counterclockwise.
- Counterclockwise
Counterclockwise rotation is typically represented by a positive angle (e.g., +45°). - Clockwise
Clockwise rotation is represented by a negative angle (e.g., -45°).
Rotation Equations
The rotation of a point \( P(x, y) \) about the origin \( O \) is given by the following system of equations: $$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y' = x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$
Rotation formulas provide the coordinates P'(x′,y′) of a point P(x;y) after it has been rotated around the origin (0,0) by a certain angle α.
The formulas are especially straightforward when the rotation is by a right angle, that is, α=90°.
- Rotation by a right angle clockwise
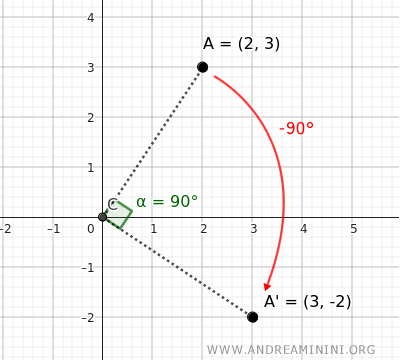
When you rotate a point P(x;y) 90° clockwise around the origin O(0;0), the result is a point P'(x';y') where the new x′ coordinate corresponds to the old y coordinate, and the new y′ coordinate is the negative of the old x coordinate. $$ \begin{cases} x' = y \\ \\ y'=-x \end{cases} $$Example. Rotate point A=(2;3) by 90° clockwise (-90°). Applying the formula above gives point A'=(3;-2).
- Rotation by a right angle counterclockwise
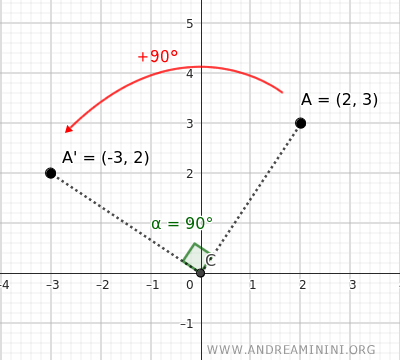
In this case, rotating a point P(x;y) 90° counterclockwise around the origin O(0;0) produces a new point P'(x';y') where the new x′ coordinate is the negative of the old y coordinate, and the new y′ coordinate corresponds to the old x coordinate. $$ \begin{cases} x' = -y \\ \\ y'=x \end{cases} $$Example. To rotate point A=(2;3) by 90° counterclockwise (+90°), use the previous rotation formula. After applying the formula, the new coordinates of the point are A'=(-3;2).
In both cases, the original coordinates are "swapped" with the addition of a negative sign depending on the direction of rotation.
In general, rotation by an angle α around the origin can be achieved using this formula:
$$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y'= x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$
This system of equations can also be represented in vector form as:
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos \alpha & - \sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$
The matrix with the trigonometric functions (sine and cosine) is known as the rotation matrix.
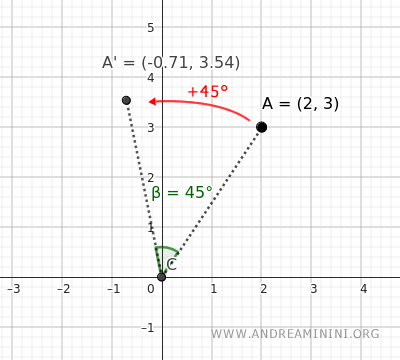
Example. Rotate point A=(2;3) by 45° counterclockwise (+45°). Use the previous rotation formula: $$ \begin{cases} x' = x \cdot \cos \alpha - y \cdot \sin \alpha \\ \\ y'= x \cdot \sin \alpha + y \cdot \cos \alpha \end{cases} $$ Substitute the coordinates of the point A you want to rotate, which are x=2 and y=3 $$ \begin{cases} x' = 2 \cdot \cos \alpha - 3 \cdot \sin \alpha \\ \\ y'= 2 \cdot \sin \alpha + 3 \cdot \cos \alpha \end{cases} $$ Use the rotation angle α=45° with a positive sign because the rotation is counterclockwise. $$ \begin{cases} x' = 2 \cdot \cos 45° - 3 \cdot \sin 45° \\ \\ y'= 2 \cdot \sin 45° + 3 \cdot \cos 45° \end{cases} $$ Calculate the sine and cosine of 45°, which are approximately sin(45°)=0.71 and cos(45°)=0.71, and substitute them into the formula: $$ \begin{cases} x' = 2 \cdot 0.71 - 3 \cdot 0.71 \\ \\ y'= 2 \cdot 0.71 + 3 \cdot 0.71 \end{cases} $$ $$ \begin{cases} x' = 1.42 - 2.13 \\ \\ y'= 1.42 + 2.13 \end{cases} $$ $$ \begin{cases} x' = -0.71 \\ \\ y'= 3.54 \end{cases} $$ The coordinates of point A' after the 45° rotation are (x';y')=(-0.71;3.54).
Special Cases of Rotation
In some noteworthy cases, the rotation formulas simplify considerably:
- 90° Counterclockwise Rotation: When the angle is $\alpha = \frac{\pi}{2}$ radians, we have $\cos \alpha = 0$ and $\sin \alpha = 1$. The rotation equations reduce to: $$ \begin{cases} x' = -y \\ y' = x \end{cases} $$
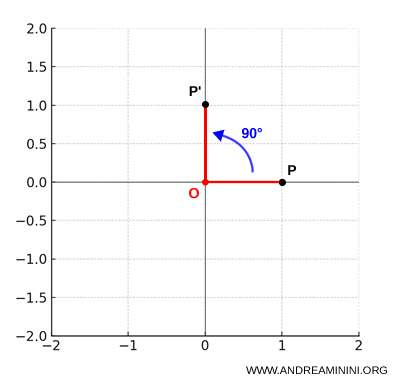
- 90° Clockwise Rotation: If the angle is $\alpha = -\frac{\pi}{2}$, then $\cos \alpha = 0$ and $\sin \alpha = -1$. The equations simplify to: $$ \begin{cases} x' = y \\ y' = -x \end{cases} $$
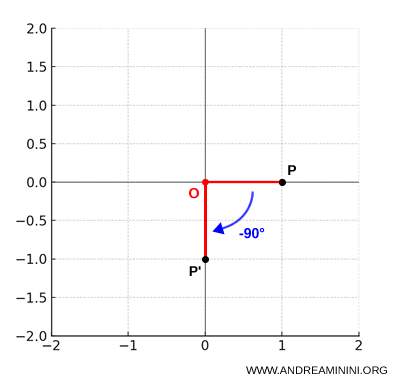
- No Rotation or Full Rotation: If $\alpha = 0$ or $\alpha = 2\pi$, then $\cos \alpha = 1$ and $\sin \alpha = 0$. The transformation becomes the identity: $$ \begin{cases} x' = x \\ y' = y \end{cases} $$
Proof
Let’s derive the rotation formulas step by step.
We begin with a point P(x, y) in the plane and consider the segment $ \overline{OP} $ that connects the origin O to point P.
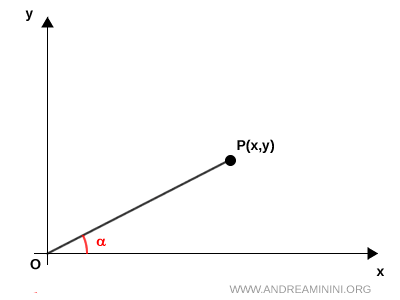
This segment forms an angle $ \alpha $ with the positive x-axis.
The coordinates of point $ P $ can be expressed in polar form as:
$$ x = \overline{OP} \cdot \cos \alpha $$
$$ y = \overline{OP} \cdot \sin \alpha $$
Here, $ \overline{OP} $ represents the length of the segment, i.e., the distance between points O and P.

Now, we rotate the segment $ \overline{OP} $ counterclockwise by an angle $ \beta $, using the origin O as the center of rotation.
After the rotation, point P moves to a new position with coordinates $ P'(x', y') $.
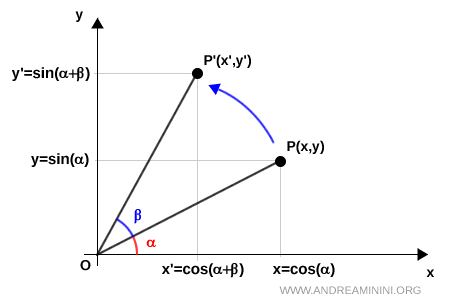
The new coordinates of $ P' $ are given by:
$$ x' = \overline{OP'} \cdot \cos ( \alpha + \beta ) $$
$$ y' = \overline{OP'} \cdot \sin ( \alpha + \beta ) $$
We now apply the angle addition formulas for cosine and sine:
$$ x' = \overline{OP'} \cdot [ \cos \alpha \cos \beta - \sin \alpha \sin \beta ] $$
$$ y' = \overline{OP'} \cdot [ \sin \alpha \cos \beta + \cos \alpha \sin \beta ] $$
Expanding the products yields:
$$ x' = \overline{OP'} \cos \alpha \cos \beta - \overline{OP'} \sin \alpha \sin \beta $$
$$ y' = \overline{OP'} \sin \alpha \cos \beta + \overline{OP'} \cos \alpha \sin \beta $$
Since rotation preserves distances, we have $ \overline{OP} = \overline{OP'} $, as rotation is an isometry. We can therefore replace $ \overline{OP'} $ with $ \overline{OP} $:
$$ x' = \overline{OP} \cos \alpha \cos \beta - \overline{OP} \sin \alpha \sin \beta $$
$$ y' = \overline{OP} \sin \alpha \cos \beta + \overline{OP} \cos \alpha \sin \beta $$
Now recall that $ x = \overline{OP} \cos \alpha $ and $ y = \overline{OP} \sin \alpha $. Substituting these expressions into the equations gives:
$$ x' = \underbrace{ \overline{OP} \cos \alpha }_{x} \cos \beta - \underbrace{ \overline{OP} \sin \alpha }_{y} \sin \beta $$
$$ y' = \underbrace{ \overline{OP} \sin \alpha }_{y} \cos \beta + \underbrace{ \overline{OP} \cos \alpha }_{x} \sin \beta $$
Which simplifies to:
$$ x' = x \cos \beta - y \sin \beta $$
$$ y' = x \sin \beta + y \cos \beta $$
Rewriting to emphasize the linear combination of $x$ and $y$:
$$ x' = x \cos \beta - y \sin \beta $$
$$ y' = x \sin \beta + y \cos \beta $$
We have thus derived the standard formulas for rotating a point about the origin by an angle $ \beta $.
Note. To recover the original coordinates of a point after a rotation, simply apply a rotation by the negative angle \( -\beta \). This leads to the following expressions: $$ \begin{aligned} x &= x' \cos(-\beta) - y' \sin(-\beta) \\ y &= x' \sin(-\beta) + y' \cos(-\beta) \end{aligned} $$ Using the trigonometric identities \( \cos(-\beta) = \cos(\beta) \) and \( \sin(-\beta) = -\sin(\beta) \), we arrive at the inverse rotation formulas: $$ \begin{aligned} x &= x' \cos \beta + y' \sin \beta \\ y &= -x' \sin \beta + y' \cos \beta \end{aligned} $$
Rotation Around Any Point
Rotating a point around a center of rotation (x0, y0) other than the origin is done using this formula: $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$
In other words, to rotate a point around a center of rotation other than the origin, such as a point (x0, y0), you must first translate the system so that (x0, y0) becomes the origin.
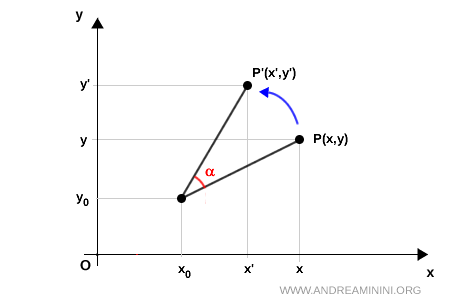
Then apply the rotation, and finally translate back to the original system.
- Translate to the new origin (x0, y0): $$ x_{temp} = x-x_0 \\ y_{temp} = y-y_0 $$
- Rotate around the origin at the translated point: $$ \begin{cases} x'_{temp} = x_{temp} \cdot \cos \alpha - y_{temp} \cdot \sin \alpha \\ y'_{temp} = x_{temp} \cdot \sin \alpha + y_{temp} \cdot \cos \alpha \end{cases} $$
- Translate back to the original system: $$ x' = x'_{temp} + x_0 \\ y' = y'_{temp} + y_0 $$
By combining these geometric transformations, you can derive the formulas for rotation around any arbitrary point (x0, y0).
$$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$
This formula represents the general rule for rotation in the plane and can be applied in any situation.
For example, if you choose the center of rotation as the point x0=0 and y0=0, the formula simplifies to the one for rotation around the origin.
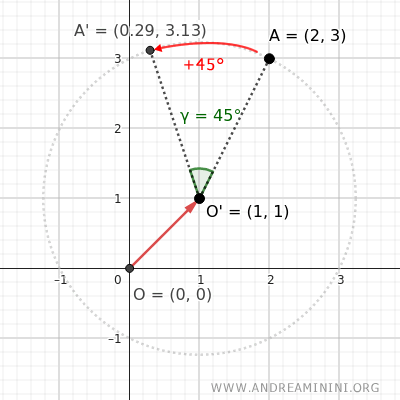
Example. In this example, rotate point A=(2;3) by 45° counterclockwise (+45°) around the point O'=(1;1) instead of the origin O=(0;0). Apply the previous rotation formula: $$ \begin{cases} x' = (x - x_0) \cdot \cos \alpha - (y - y_0) \cdot \sin \alpha + x_0 \\ \\ y' = (x - x_0) \cdot \sin \alpha + (y - y_0) \cdot \cos \alpha + y_0 \end{cases} $$ Substitute the coordinates of the rotation center x0=1 and y0=1: $$ \begin{cases} x' = (x - 1) \cdot \cos \alpha - (y - 1) \cdot \sin \alpha + 1 \\ \\ y' = (x - 1) \cdot \sin \alpha + (y - 1) \cdot \cos \alpha + 1 \end{cases} $$ Now, substitute the coordinates of the point A you want to rotate, which are x=2 and y=3: $$ \begin{cases} x' = (2 - 1) \cdot \cos \alpha - (3 - 1) \cdot \sin \alpha + 1 \\ \\ y' = (2 - 1) \cdot \sin \alpha + (3 - 1) \cdot \cos \alpha + 1 \end{cases} $$ $$ \begin{cases} x' = 1 \cdot \cos \alpha - 2 \cdot \sin \alpha + 1 \\ \\ y' = 1 \cdot \sin \alpha + 2 \cdot \cos \alpha + 1 \end{cases} $$ Substitute the rotation angle α=45° counterclockwise: $$ \begin{cases} x' = 1 \cdot \cos 45° - 2 \cdot \sin 45° + 1 \\ \\ y' = 1 \cdot 0.71 + 2 \cdot 0.71 + 1 \end{cases} $$ Knowing that the sine and cosine of 45° are approximately sin(45°)=0.71 and cos(45°)=0.71: $$ \begin{cases} x' = 1 \cdot 0.71 - 2 \cdot 0.71 + 1 \\ \\ y' = 1 \cdot 0.71 + 2 \cdot 0.71 + 1 \end{cases} $$ $$ \begin{cases} x' = 0.71 - 1.42 + 1 \\ \\ y' = 0.71 + 1.42 + 1 \end{cases} $$ $$ \begin{cases} x' = 0.29 \\ \\ y' = 3.13 \end{cases} $$ The new coordinates of point A' after the rotation are x'=0.29 and y=3.13.
Rotation in Space
To rotate a solid in space, we select a line \( r \), known as the axis of rotation, a plane \( \pi \) perpendicular to this line, and a rotation angle \( \alpha \).
This transformation maps each point \( P \) of the solid to a corresponding point \( P' \), which lies in the same plane \( \pi \).
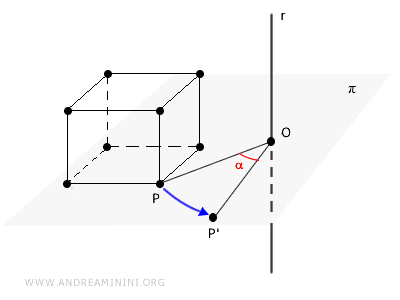
All points along the axis \( r \) remain fixed (referred to as invariant points), meaning their position does not change regardless of the rotation.
Every other point in the solid moves along a circular path within the plane \( \pi \), centered at a point \( O \) on the axis \( r \), where the axis intersects the plane. The radius of this circle is the distance \( \overline{OP} \) between \( P \) and \( r \).
The new position of \( P' \) is determined by the rotation angle \( \alpha \), which defines the amount of rotation around the center \( O \) of the circle.
Mathematically, if the axis of rotation coincides with one of the Cartesian axes, the transformation is described by a rotation matrix. For example, rotating a point by an angle \( \alpha \) around the \( z \)-axis results in new coordinates \( (x', y', z') \) given by:
\[
\begin{cases}
x' = x \cos \alpha - y \sin \alpha \\
y' = x \sin \alpha + y \cos \alpha \\
z' = z
\end{cases}
\]
Similar formulas apply to rotations around the \( x \)- and \( y \)-axes. For rotations around an arbitrary axis, the transformation can be determined using general rotation matrices.
Rotation Matrix
In the two-dimensional plane, a rotation by an angle $ \theta $ around the origin can be represented by a 2×2 orthogonal matrix belonging to the special group $ SO(2) $.
$$
R(\theta) =
\begin{pmatrix}
\cos\theta & -\sin\theta\\[4pt]
\sin\theta & \cos\theta
\end{pmatrix}
$$
When this matrix is applied to a vector in the plane, $ \mathbf{r} = \begin{pmatrix} x \\ y \end{pmatrix} $, it produces the rotated vector:
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} =
\mathbf{r}' = R(\theta)\,\mathbf{r} =
\begin{pmatrix}
\cos\theta & -\sin\theta\\[4pt]
\sin\theta & \cos\theta
\end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} =
\begin{pmatrix}
x\cos\theta - y\sin\theta\\[4pt]
x\sin\theta + y\cos\theta
\end{pmatrix}
$$
This expression corresponds to the familiar system of equations for a planar rotation, now written in compact matrix form:
$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix}
x\cos\theta - y\sin\theta\\[4pt]
x\sin\theta + y\cos\theta
\end{pmatrix} \Leftrightarrow \begin{cases} x' = x \cdot \cos \theta - y \cdot \sin \theta \\ \\ y'= x \cdot \sin \theta + y \cdot \cos \theta \end{cases} $$
This transformation preserves the distance from the origin, since the magnitude of the vector remains unchanged:
$$ d = \sqrt{ x'^2 + y'^2 } = \sqrt{ x^2 + y^2 } $$
In other words, it represents a pure rotation, with no stretching or reflection, belonging to the group $ SO(2) $.
Example. Let’s rotate the point \( A = (2,\,3) \) by \( 45^\circ \) counterclockwise (a positive angle) about the origin $ O = (0,0) $. The corresponding rotation matrix is:
$$ R(45^\circ)= \begin{pmatrix} \cos45^\circ & -\sin45^\circ\\[4pt] \sin45^\circ & \cos45^\circ \end{pmatrix} = \begin{pmatrix} \frac{\sqrt2}{2} & -\frac{\sqrt2}{2}\\[4pt] \frac{\sqrt2}{2} & \frac{\sqrt2}{2} \end{pmatrix} $$The distance of point $A$ from the origin is:
$$ |A| = \sqrt{ x^2+y^2} = \sqrt{2^2+3^2} = \sqrt{13} $$
Applying the rotation to the position vector \( \mathbf r = \begin{pmatrix}2\\[2pt]3\end{pmatrix} \), we get:
$$ \mathbf r' = R(45^\circ)\,\mathbf r = \begin{pmatrix} \frac{\sqrt2}{2} & -\frac{\sqrt2}{2}\\[4pt] \frac{\sqrt2}{2} & \frac{\sqrt2}{2} \end{pmatrix} \begin{pmatrix} 2\\[2pt]3 \end{pmatrix} = \begin{pmatrix} \frac{2\sqrt2}{2}-\frac{3\sqrt2}{2}\\[4pt] \frac{2\sqrt2}{2}+\frac{3\sqrt2}{2} \end{pmatrix} = \begin{pmatrix} -\tfrac{\sqrt2}{2}\\[4pt] \tfrac{5\sqrt2}{2} \end{pmatrix} $$After the \(45^\circ\) counterclockwise rotation, the point \(A(2,3)\) moves to:
$$ A'(x',y') = \left(-\tfrac{\sqrt2}{2},\,\tfrac{5\sqrt2}{2}\right) $$ $$ A'(x',y') = \left(-0.71, 3.54\right) $$This shows how the vector rotates in the plane.
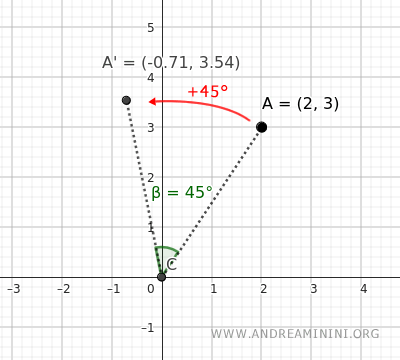
The distance from the origin remains constant, as expected for any pure rotation:
$$ |A'| = \sqrt{ x'^2+y'^2} = \sqrt{(-0.71)^2+(3.54)^2} \approx \sqrt{13} $$
The Rotation Matrix in Three-Dimensional Space
In three-dimensional space, a rotation is represented by a 3×3 orthogonal matrix with determinant equal to 1, that is, an element of the special group $ SO(3) $ (the Special Orthogonal Group in three dimensions).
The general expression for a rotation through an angle $ \theta $ around a unit axis \( \hat{n} = (n_x, n_y, n_z) \) is given by:
$$
R(\hat{n}, \theta) =
\begin{pmatrix}
\cos\theta + n_x^2(1 - \cos\theta) & n_x n_y(1 - \cos\theta) - n_z \sin\theta & n_x n_z(1 - \cos\theta) + n_y \sin\theta \\[6pt]
n_y n_x(1 - \cos\theta) + n_z \sin\theta & \cos\theta + n_y^2(1 - \cos\theta) & n_y n_z(1 - \cos\theta) - n_x \sin\theta \\[6pt]
n_z n_x(1 - \cos\theta) - n_y \sin\theta & n_z n_y(1 - \cos\theta) + n_x \sin\theta & \cos\theta + n_z^2(1 - \cos\theta)
\end{pmatrix}.
$$
This is known as the Rodrigues rotation formula, which provides a compact and elegant representation of any 3D rotation.
Let’s look at some important special cases:
1] Rotation about the x-axis
$$
R_x(\theta) =
\begin{pmatrix}
1 & 0 & 0\\
0 & \cos\theta & -\sin\theta\\
0 & \sin\theta & \cos\theta
\end{pmatrix}.
$$
2] Rotation about the y-axis
$$
R_y(\theta) =
\begin{pmatrix}
\cos\theta & 0 & \sin\theta\\
0 & 1 & 0\\
-\sin\theta & 0 & \cos\theta
\end{pmatrix}.
$$
3] Rotation about the z-axis
$$
R_z(\theta) =
\begin{pmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0\\
0 & 0 & 1
\end{pmatrix}.
$$
Every rotation matrix in $SO(3)$ preserves both vector lengths and the angles between them, since $ |\mathbf{r}'| = |\mathbf{r}| $ and $ \mathbf{r}' \cdot \mathbf{s}' = \mathbf{r} \cdot \mathbf{s} $. Its determinant is $ +1 $, and its inverse equals its transpose, that is $ R^{-1} = R^{T} $.
Observations
Here are some important points about rotation:
- Rotation is an isometry
Given any two points A and B, and their images A′ and B′ under a rotation, the distance between them remains unchanged. In other words, the segments AB and A′B′ are congruent: AB ≅ A′B′.
Proof. Let \( A \) and \( B \) be arbitrary points in the plane, and let \( O \) be a fixed point. Consider a rotation about \( O \) by an angle \( \theta \), which maps \( A \) and \( B \) to \( A' \) and \( B' \), respectively.
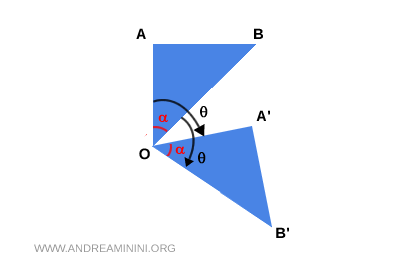
Since a rotation preserves distances from the center, we have \( OA \cong OA' \) and \( OB \cong OB' \). Moreover, because rotations preserve angles, it follows that \( \angle AOB \cong \angle A'OB' \). Therefore, triangles \( OAB \) and \( OA'B' \) are congruent by the Side-Angle-Side (SAS) congruence criterion. As a result, their corresponding sides are equal, so \( AB = A'B' \). Since \( AB \) is the original distance and \( A'B' \) is the distance between the images, this confirms that a rotation preserves distance - hence, it is an isometry. - A rotation of zero degrees or a multiple of 360° is an identity transformation
In the plane, a rotation of 0° or any multiple of 360° is equivalent to the identity operation. This is because such a rotation does not alter the position of the figure. In other words, a rotation of zero or any multiple of a full turn results in a invariant figure on the plane.
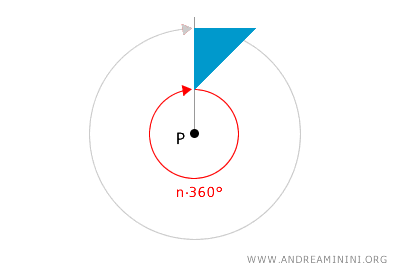
A figure is considered "fixed" if all its points remain in the same position on the plane after a geometric transformation.
- In a rotation, the center of rotation remains a fixed point
In any rotation, the center of rotation P remains in the same position on the plane. Therefore, the center of rotation is always a fixed point.
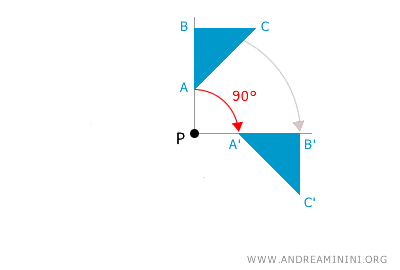
A point is considered "fixed" if it stays in the same position on the plane after a geometric transformation.
- Rotation has no globally invariant lines
For a rotation about a point by any angle other than 0° or 360°, no line remains globally invariant: every line is carried to a different line in a new position.Note. Only a rotation through a whole number of full turns (k·360°), which is just the identity transformation, leaves all lines not only globally invariant but also pointwise invariant, since every point stays fixed.
- The circumference and circle remain fixed under any rotation about their center
Under any rotation about their center, the circumference and circle do not change their position on the plane. - A square remains fixed under rotation by multiples of a right angle about its center
A square remains in the same position on the plane after being rotated around its center, which is the intersection of its diagonals, by any angle that is a multiple of a right angle (90°). - In the plane, a rotation of ±180° is equivalent to central symmetry
A rotation of 180° (a straight angle) about a point P is equivalent to central symmetry with respect to the same point P. When a figure is rotated by 180° about a point, every point of the figure is moved to a position directly opposite to the center of rotation while maintaining the same distance from P. This behavior is identical to what occurs with central symmetry, where each point is mapped to a point directly opposite the center of symmetry. Therefore, a rotation of ±180° ( ±π radians) and central symmetry about the same point are equivalent geometric transformations. A rotation of ±180° is also known as a "half-turn" or "opposition."
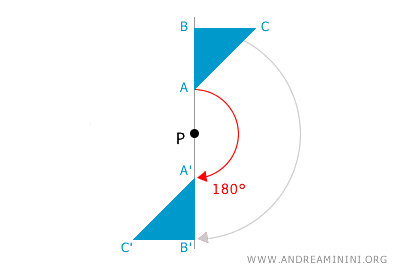
- In three-dimensional space, a 180° rotation is equivalent to axial symmetry
In three-dimensional space, a 180° rotation corresponds to axial symmetry. This means that when a 3D object is rotated by 180° around an axis, every point of the object is reflected across that axis, resulting in a symmetric position. It’s as if the object has been "flipped" around the axis of rotation. - Composition of Rotations
The composition of two or more rotations r(P;α) and r(P;β) with the same center of rotation P is equivalent to a single rotation with center P and an angle equal to the sum of the rotation angles α and β, that is, r(P; α+β).
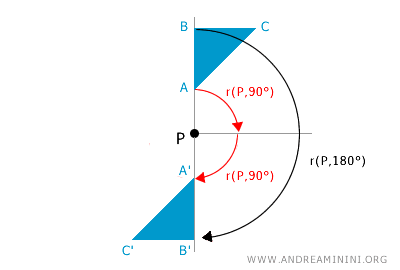
In general, the composition of rotations is not necessarily an operation within rotations because if the centers of rotation differ, the composition of two or more rotations does not always result in a single rotation. Here’s an example of composing two rotations of the same figure but with different centers of rotation P and P'.
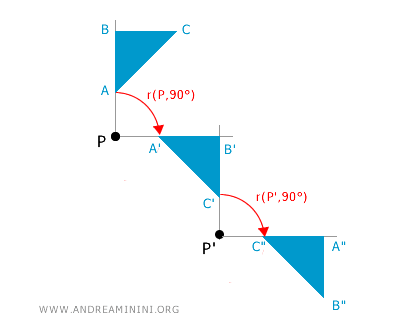
The composition of two rotations with angles \( \alpha_1 \) and \( \alpha_2 \), centered at distinct points \( P \) and \( P' \), may result in either a new rotation - typically with a different center and total angle \( \alpha_1 + \alpha_2 \) - or in a translation. Thus, in general, the composition of two rotations about different centers does not produce another rotation. By contrast, when both rotations share the same center \( P \), their composition is always a rotation about \( P \) with angle \( \alpha_1 + \alpha_2 \). - Rotations in the plane with the same center form a commutative group
When two consecutive rotations in the plane share the same center of rotation P, the result is always another rotation with the same center. Therefore, rotation in the plane is a closed operation, as the result remains within the set of rotations. The order in which the rotations are applied does not affect the final result. In other words, rotating by α degrees followed by β degrees is equivalent to rotating by β degrees followed by α degrees. Because of this, rotation in the plane satisfies the commutative property, and rotations in the plane form a commutative group (Abelian group). - The determinant of a rotation matrix is always 1
In the plane, the rotation matrix for an angle $\alpha$ is given by: $$ R(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{pmatrix} $$ Its determinant is calculated as follows: $$ \det(R(\alpha)) = \cos \alpha \cdot \cos \alpha - (-\sin \alpha) \cdot \sin \alpha = \cos^2 \alpha + \sin^2 \alpha = 1 $$ This result reflects the fundamental trigonometric identity $ \cos^2 \alpha + \sin^2 \alpha = 1 $. Hence, the determinant of a rotation matrix is always 1, regardless of the value of $\alpha$.Note. This confirms that a rotation is an isometry - it preserves distances - and also preserves area, since the absolute value of the determinant is 1. Moreover, because the determinant is positive, the transformation preserves orientation, unlike a reflection, which would have a determinant of -1 and thus reverse orientation.
And so on.
