Geometric Identity Transformation

Identity is a geometric transformation where every point on the plane (or in space) maps to itself, meaning nothing moves or changes.

This is the simplest possible type of geometric transformation.

In other words, it’s like saying, "I want to transform this shape," but then doing absolutely nothing. The shape stays exactly as it is, without any shift, rotation, or resizing.

$$ \forall \ P \ \ ,  \ \ P = f(P) $$

In mathematical terms, it's like multiplying a shape by 1. No matter what you multiply by 1, it remains unchanged. $$ \forall \ x \ \ ,  \ \ x = f(x \cdot 1) $$ In geometry, this is what identity means: a transformation that leaves everything exactly as it was.

A Practical Example

Let’s take a geometric shape, like a square.

Now, apply a 360° rotation (a full turn) to the shape.

The result is that every point remains exactly where it started.

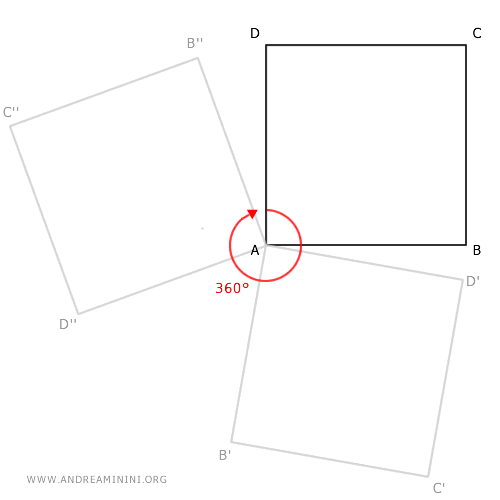
After the full rotation, point B is back at its original coordinates. The same is true for all other points.

$$ B = f(B)  $$

$$ C = f(C)  $$

$$ D = f(D)  $$

This is a classic example of a geometric identity.

Other examples include two full rotations (720°) or any multiple of a complete turn. Another example is a rotation with a zero angle (0°). In all these cases, the points stay in their original positions.

And so on.