Invariants of Geometric Transformations

Invariants in a geometric transformation are properties that remain unchanged ("invariant") when a figure undergoes that transformation.

The specific invariants depend on the type of transformation being applied.

Each type of geometric transformation has its own set of invariants.

Why are they important? Identifying invariants is key to understanding the properties of geometric figures and how they behave under different transformations.

A Practical Example

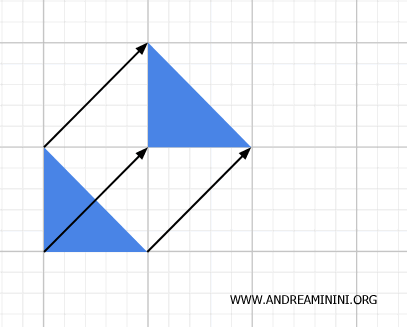
In a translation, every point of a figure moves in the same direction by the same distance.

As a result, the distances between points, as well as the shape, size, and orientation of the figure, remain unchanged.

Example 2

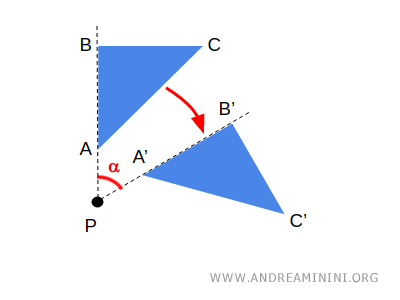
In a rotation, a figure rotates around a fixed point, P.

In this case, the invariants are the fixed point, the distances between points, and the figure’s shape and size.

Example 3

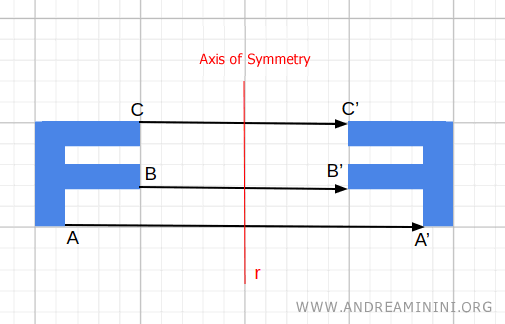
In a reflection, a figure is flipped across a line known as the axis of reflection.

The invariants in reflection are the distances between points, the shape, and the size.

Note: In general, an isometry (e.g., translation, rotation, reflection) is a geometric transformation that preserves the distances between all pairs of points, also known as "rigid motions." As such, distances, shape, and size are invariant properties of any isometry.

Example 4

In a homothety (scaling), a figure is scaled relative to a fixed point called the center of homothety.

In this case, the invariants are the ratio of distances between points relative to the center of homothety, and the shape, though not the absolute size of the figure.

Note: Homothety is not an isometry. Unlike isometries, homothety changes the absolute distances between points, and therefore the size of the figure, while still preserving its proportions and shape.

And so on.